黑箱优化与强化学习（EEee227c Lecture20学习笔记）

在本讲中，主要学习的是无导数优化，并从无导数优化自然过渡到强化学习。

本读书笔记阅读了相关资料，并且使用 Matlab 语言独立实现了其中的实验。

Matlab 语言要求所有函数都定义在代码的最后，但是为了阅读顺畅，本文档修改了部分代码的顺序。如果需要运行代码，请下载源代码文件。

[toc]

黑箱优化

在本讲中，我们将研究所谓的黑箱优化、无导数优化或零阶优化。

这里的一般目标是解决一个问题

\[ \min_{x} f(x), \]

可能在约束集 \(x\in\Omega\) 上，其中我们无法求函数 \(f\colon\mathbb{R}^n\to\mathbb{R}\) 的梯度。我们只能对某个点 \(x\in\Omega\) 并计算函数值 \(f(x)\in\mathbb{R}\)。

基本随机搜索

随机搜索

选择一个初始点 \(x_0\)

从 \(t=1\) 开始迭代： 1. 选择 \(d_t\) 作为 \(\mathbb{R}^n\) 中的一个随机方向。

  1. 设置 \(\eta^* = \arg\min_\eta f(x_{t-1}+\eta d_t)\)

  2. 令 \(x_t = x_{t-1} + \eta^* d_t\)

分析

我们将看到，对于这个算法，基本上梯度下降的所有性质都成立，只是迭代次数多了一个因子 \(n\)。假设 \(f\) 是一个 \(\beta\)-李普希兹的的可微凸函数。

对于任意 \(\eta\)，根据泰勒展开和光滑性，有：

\[ f(x_t + \eta d_t) \le f(x_t) + \eta \langle d_t, \nabla f(x_t) \rangle + \frac{\eta^2\beta}{2}\|d_t\|^2 \]

因此，通过最小化上界，存在一个步长 \(\eta\)，使得

\[ f(x_t + \eta d_t) \le f(x_t) - \frac{1}{\beta}\langle d_t, \nabla f(x_t)\rangle^2 \|d_t\|^2 \]

此外，我们实际采取的步长只会更好：

\[ f(x_t + \eta^* d_t) \le f(x_t + \eta d_t). \]

取期望后得到

\[ \mathbb{E}[f(x_t + \eta^* d_t)] \le \mathbb{E}[f(x_t)] - \frac1{\beta n}\mathbb{E}[\|\nabla f(x_t)\|^2] \]

这看起来与梯度下降法非常相似，只是多了一个因子 \(n\)。于是： - 对于凸函数，我们得到 \(n\beta/\epsilon\) 的速率。 - 对于强凸函数，我们得到 \(n\beta\log(1/\epsilon)\) 的速率。 - 对于非凸函数，我们收敛到一个驻点。

基本上，它比该函数类上的梯度方法的复杂度多了 \(n\) 倍。

线搜索问题

正如所述，该算法在随机方向上使用最优步长。我们通常只能通过各种方式近似这个步长。我们将讨论所谓的黄金分割搜索：

黄金分割搜索是一种在指定区间内寻找函数的极值（最小值或最大值）的技术。对于在区间内有极值的严格单峰函数，它将找到那个极值，而对于包含多个极值的区间（可能包括区间边界），它将收敛到其中一个极值。如果区间上唯一的极值在区间的边界上，它将收敛到那个边界点。该方法通过连续缩小指定区间内的值范围来操作，这使得它相对较慢，但非常稳健。这种技术的名字来源于算法保持了四个点的函数值，其三个区间宽度的比例为\(\varphi:1:\varphi\)，其中\(\varphi\)是黄金比例。这些比例在每次迭代中都保持最大效率。除边界点外，在搜索最小值时，中心点总是小于或等于外围点，以确保最小值包含在外围点之间。

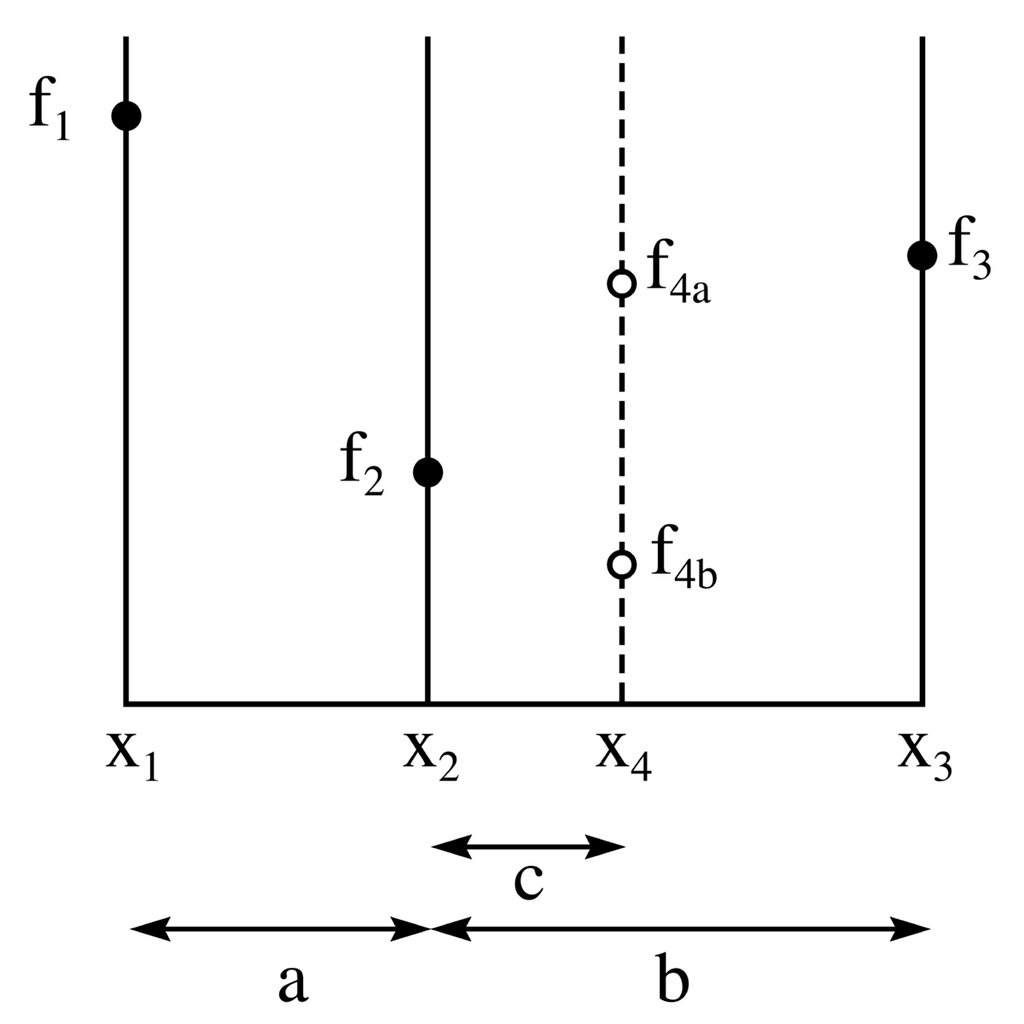
黄金分割搜索的示意图。初始的 $x$ 值三元组为 $\{x_1, x_2, x_3\}$。如果 $f(x_4) = f_{4a}$，则选择三元组 $\{x_1, x_2, x_4\}$ 进行下一次迭代。如果 $f(x_4) = f_{4b}$，则选择三元组 $\{x_2, x_4, x_3\}$。

这里的讨论是关于在单峰函数中寻找最小值。与求零点不同，求零点时，两个符号相反的函数值就可以确定一个根的范围，但是在寻找最小值时，就需要三个值。黄金分割搜索是一种逐步缩小包含最小值的区间的有效方法。关键在于，无论已经评估了多少个点，最小值都位于目前已经评估的最小值点相邻的两个点所确定的区间内。

上图说明了寻找最小值的方法中的一个步骤。纵轴是\(f(x)\) 的函数值，横轴是 \(x\) 参数。\(f(x)\) 的值已经在三个点 \(x_1, x_2\) 和 \(x_3\) 处进行了求解。由于 \(f_2\) 小于 \(f_1\) 和 \(f_3\)，很明显最小值位于 \(x_1\) 到 \(x_3\) 的区间内。

最小化过程的下一步是通过在新的 \(x\) 值 \(x_4\) 处求函数值来“探测”函数。最有效的方法是选择 \(x_4\) 位于最大的区间内，即 \(x_2\) 和 \(x_3\) 之间。从图中可以看出，如果函数在 \(x_4\) 处的值 \(f_{4 a}>f\left(x_2\right)\)，那么最小值位于 \(x_1\) 和 \(x_4\) 之间，新的三元组点将是 \(x_1, x_2\) 和 \(x_4\)。然而，如果函数在 \(x_4\) 处的值 \(f_{4 b}<f\left(x_2\right)\)，那么最小值位于 \(x_2\) 和 \(x_3\) 之间，新的三元组点将是 \(x_2, x_4\) 和 \(x_3\)。因此，在任何情况下，我们都可以构造一个新的更窄的搜索区间，该区间保证包含函数的最小值。

从上图可以看出，新的搜索区间要么在 \(x_1\) 和 \(x_4\) 之间，长度为 \(a+c\)，要么在 \(x_2\) 和 \(x_3\) 之间，长度为 \(b\)。黄金分割搜索要求这些区间相等。如果它们不相等，一连串的“坏运气”可能导致较宽的区间被多次使用，从而减慢收敛速度。为了确保 \(b=a+c\)，算法应选择 \(x_4=x_1+\left(x_3-x_2\right)\)。

然而，仍然存在 \(x_2\) 相对于 \(x_1\) 和 \(x_3\) 的位置问题。黄金分割搜索选择这些点之间的间距，使得这些点与随后的三元组 \(x_1, x_2, x_4\) 或 \(x_2, x_4, x_3\) 具有相同的间距比例。通过在整个算法中保持相同的间距比例，我们避免了 \(x_2\) 非常接近 \(x_1\) 或 \(x_3\) 的情况，并保证在每一步中区间宽度按相同的常数比例缩小。

从数学上讲，为了确保在评估 \(f\left(x_4\right)\) 后，间距与评估前的间距成比例，如果 \(f\left(x_4\right)\) 是 \(f_{4 a}\)，并且我们的新三元组点是 \(x_1, x_2\) 和 \(x_4\)，那么我们希望

\[ \frac{c}{a}=\frac{a}{b} . \]

然而，如果 \(f\left(x_4\right)\) 是 \(f_{4 b}\)，并且我们的新三元组点是 \(x_2, x_4\) 和 \(x_3\)，那么我们希望

\[ \frac{c}{b-c}=\frac{a}{b} . \]

从这两个同时方程中消去 \(c\)，得到

\[ \left(\frac{b}{a}\right)^2-\frac{b}{a}=1 \]

或

\[ \frac{b}{a}=\varphi \]

其中 \(\varphi\) 是黄金比例：

\[ \varphi=\frac{1+\sqrt{5}}{2} \]

评估点之间间距比例中黄金比例的出现，正是这个搜索算法得名的原因。

算法的代码实现如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function x_min = gss(f, a, b, tol)
    % 黄金分割搜索
    % 求函数f在[a,b]之间的最小值
    % f: 函数句柄，待求函数
    % a: 实数，区间下界
    % b: 实数，区间上界
    % tol: 收敛容差
    
    if nargin < 4
        tol = 1e-5; 
    end
    
    gr = (sqrt(5) + 1) / 2;
    c = b - (b - a) / gr;
    d = a + (b - a) / gr;
    
    while abs(c - d) > tol
        if f(c) < f(d)
            b = d;
        else
            a = c;
        end
        c = b - (b - a) / gr;
        d = a + (b - a) / gr;
    end
    
    x_min = (b + a) / 2;
end

有了行搜索，我们就可以编写随机搜索算法的代码了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function iterates = random_search(oracle, init, num_steps, line_search)
    % 实现随机搜索。
    
    % oracle: 函数句柄，待求函数。
    % init: 列向量，oracle 定义域中的点，迭代起始点。
    % num_steps: 整数，迭代次数。
    % line_search: 线搜索方法（默认为黄金分割搜索）。
    
    if nargin < 4
        line_search = @gss;
    end
    
    iterates = [init];
    for i = 1:num_steps
        d = randn(size(init)) .* 100;
        d = d / norm(d);
        x = iterates(:,end);
        size(x)
        eta = line_search(@(step) oracle(x + step * d), -1, 1);
        iterates = [iterates, x + eta * d];
        size(iterates)
    end
end

在简单的最小二乘问题上检验一下方法的正确性：

1
2
3
4
5
6
7
8
9
function error = least_squares(x, A, b)
    % 计算最小二乘误差。
    
    % x: 列向量，自变量
    % A: 矩阵
    % b: 列向量
    
    error = 0.5 * norm(A * x - b)^2;
end
1
2
3
4
5
6
7
8
9
10
11
12
A = randn(100, 100);
b = randn(100, 1);

xs = random_search(@(x)least_squares(x,A,b), b, 1000, @gss);

% 绘制误差图
ys = arrayfun(@(i) least_squares(xs(:, i),A,b), 1:size(xs, 2));
plot(ys);
xlabel('Iteration');
ylabel('Error');
title('Error Plot');

Nelder-Mead法

内尔德和米德提出了一种更复杂的随机搜索变体。在Matlab中，可以直接调用fminsearch函数，其中的内核即为Nelder-Mead法。

让我们在一个常见的非凸测试函数上测试： \[ H(\boldsymbol{x})=(x_1^2+x_2-11)^2+(x_1+x_2^2-7)^2 \]

1
2
3
4
5
function ans=himmelblau(X)
    % 非凸函数
    % x: 列向量，自变量
    ans = (X(1).^2 + X(2) - 11).^2 + (X(1) + X(2).^2 - 7).^2;
end

可以画出这个函数的图像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
points = linspace(-5, 5, 100);
[X, Y] = meshgrid(points, points); % 生成网格数据
Z = zeros(size(X));
for i=1:numel(X)
    vector_input=[X(i);Y(i)];
    Z(i)=himmelblau(vector_input);
end
% 创建图形和轴
fig = figure('Position', [100, 100, 800, 800]); % 设置图形窗口大小
ax = axes('Parent', fig, 'Projection', 'orthographic'); 

% 绘制曲面图
surf(ax, X, Y, Z, 'FaceColor', 'interp', 'EdgeColor', 'none');
xlabel('X'); % X轴标签
ylabel('Y'); % Y轴标签
zlabel('Z'); % Z轴标签
title('Himmelblau''s Function'); % 图形标题

使用Nelder-Mead法求解最小值：

1
2
3
4
options = optimset('Display','iter','PlotFcns',@myplot);
x0 = [1;1];
fun = @himmelblau;
[x,fval,exitflag,output] = fminsearch(fun,x0,options)

其中，myplot为适配fminsearch函数而写的自定义绘图函数，实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function stop = myplot(x,optimValues,state)
    stop = false;
    persistent points steps;
    switch state
        case 'init'
              % Setup for plots or dialog boxes
              hold on
        case 'iter'
              % Make updates to plots or dialog boxes as needed
              plot(optimValues.iteration,optimValues.fval,'bx');
              points=[points,optimValues.fval];
              steps = [steps,optimValues.iteration];
        case 'done'
              % Cleanup of plots, dialog boxes, or final plot
              plot(steps,points);
              hold off
    end
end

运行结果：

Nelder-Mead法

随机搜索在这里的效果也不错：

1
2
3
4
5
6
7
xs = random_search(@himmelblau,[1;1], 50);
ys = arrayfun(@(i) himmelblau(xs(:, i)), 1:size(xs, 2));
figure;
plot(ys);
xlabel('Iteration');
ylabel('Error');
title('Error Plot');
随机搜索

强化学习

考虑一个抽象的动态系统模型

\[ x_{t+1} = f(x_t, u_t, e_t)\,. \]

这里，\(x_t\) 是系统的状态，\(u_t\) 是控制动作，\(e_t\) 是随机扰动。我们将假设 \(f\) 是固定的但未知的。

轨迹是由这个动态系统生成的状态和控制动作的序列。

\[ \tau_t = (u_1,…,u_{t-1},x_0,…,x_t) \,. \]

控制策略是一个函数 \(\pi\)，它接受一个来自动态系统的轨迹并输出一个新的控制动作。注意，\(\pi\) 只能访问之前的状态和控制动作。

Flappy bird 动力系统

想象我们有一只以恒定速度飞行的小鸟。它的垂直位置 \(h\) 由重力和空气阻力控制。因此，总的向下力为 \(F = mg - kv\)，其中 \(g\) 是重力加速度，\(v\) 是向下的速度，\(k\) 是与速度相关的阻力系数。使用 \(F=ma\)，这给出了一阶微分方程 \[ \frac{dv}{dt} = g - (k/m)v \] 这只鸟可以选择加速向上飞。它试图避免撞到地面 \(h=0\)，同时最小化向上的加速度。

据此，我们建立这个动力系统的数学模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
function [new_state] = flappy_bird(state, action)
    % Flappy bird 动态系统。
    % 输入: 
        % state: 2维列向量，下降速度和高度
        % action: 实数，向上加速度
    % 返回: 
        % new_state: 列向量，新的下降速度和高度
        
    v = state(1); % 下降速度
    h = state(2); % 高度
    g = 1; % 重力加速度
    k = 0.01; % 阻力系数
    m = 1; % 质量
    new_state = [v + g - (k/m)*v - action; h - v]; % 计算新的速度和高度
end

function [states, actions] = unroll(system, init_state,init_action, policy, num_steps)
    % 展开动态系统。
    % 输入: 
        % system: 函数句柄，动力系统
        % init_state: 2维列向量，动力系统状态（速度和高度）
        % init_action: 实数，动力系统状态（加速度）
        % policy: 函数句柄，运动策略
        % num_steps: 整数，模拟的长度
    % 返回: 
        % states: 2行num_steps列矩阵，整个过程中的速度和高度
        % actions: num_steps维行向量，整个过程中的加速度
        
    states = init_state; % 初始化状态列表
    actions = init_action; % 初始化动作列表
    for i = 1:num_steps
        action = policy(states, actions); % 根据策略函数确定动作
        actions = [actions, action]; % 将动作添加到动作列表
        states = [states, system(states(:,end), action)]; % 更新状态
    end
end

function action = example_policy(states, actions)
    % 每5步加速向上。
    % 输入: 
        % states: 2行k列矩阵，迄今为止的速度和高度
        % actions: k维行向量，迄今为止的加速度
    % 返回: 
        % action: 实数，动作完成后的加速度
        
    v = states(1,end); % 最后一个状态的速度
    h = states(2,end); % 最后一个状态的高度
    if mod(length(states), 5) == 0
        action = 7; % 每5步执行一次向上加速
    else
        action = 0; % 否则不加速
    end
end

在这里，还建立了一个简单的策略，即每模拟5步加速向上一次。

进行仿真：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
% 初始化Flappy Bird的初始状态和动作
init_action = 0;
init_state = [0;10];
num_steps = 10; % 定义展开的步数

% 展开动态系统
[states, actions] = unroll(@flappy_bird, init_state,init_action, @example_policy, num_steps);

% 提取高度数据
heights = states(2,:);

% 创建图形
fig = figure('Position', [100, 100, 750, 500]); 
ax = axes('Parent', fig);

plot(ax, 1:length(heights), heights, 'LineWidth', 2);
ylabel(ax, 'height');
xlabel(ax, 'time');
仿真10步

在短距离模拟时，它表现得好像不错。但是如果把时间放长，它就有些超过需要。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
num_steps = 20; % 定义展开的步数

[states, actions] = unroll(@flappy_bird, init_state,init_action, @example_policy, num_steps);

heights = states(2,:);

fig = figure('Position', [100, 100, 750, 500]); 
ax = axes('Parent', fig); 


% 绘制高度随时间变化的折线图
plot(ax, 1:length(heights), heights, 'LineWidth', 2);
ylabel(ax, 'height');
xlabel(ax, 'time');

从奖励中学习策略

强化学习的主要目标是解决最优控制问题：

\[ \begin{array}{ll} \mbox{maximize}_{u_t} & \mathbb{E}_{e_t}[ \sum_{t=0}^N R_t[x_t,u_t] ]\\ \mbox{subject to} & x_{t+1} = f(x_t, u_t, e_t)\\ & \mbox{($x_0$ given)} \end{array} \]

  • \(R_t[x_t,u_t]\) 是一个奖励，我们假设它是已知的，事实上它是人为设定的。
  • 函数 \(f\) 是未知的。

在我们的 Flappy Bird 示例中，撞到地面会获得一个巨大的负奖励，而向上加速会获得一个小的负奖励。

当代强化学习的主要范式是以下方法。我们决定一个策略 \(\pi\) 和视野长度 \(L\)。然后，我们要么将这个策略传递给模拟引擎，要么传递给真实的机器人系统，并获得一个轨迹

\[ \tau_L = (u_1,…,u_{L-1},x_0,…,x_L)\,, \]

其中 \(u_t = \pi(\tau_t)\)。这是我们的预言模型。我们通常希望最小化由预言模型计算的样本总数。因此，如果我们运行 \(m\) 个视野长度为 \(L\) 的查询，我们将支付总成本 \(mL\)。然而，我们可以自由地为每个实验改变视野长度。

策略梯度

在策略梯度方法中，我们假设策略是随机的，并由一组可调参数 \(\theta\) 指定。

然后，我们可以将奖励最大化问题写成一般形式的随机优化问题。令 \(p_\theta\) 表示由参数 \(\theta\) 产生的轨迹的概率分布。下面我们使用 \(\mathbb{E}_\theta\) 表示从 \(p_\theta\) 中抽取的轨迹的期望。

\[ J(\theta):=\mathbb{E}_\theta[R(u)] \]

关键思想是使用以下技巧计算 \(J(\theta)\) 的梯度。

\[ \begin{align*} \nabla_{\theta} J(\theta) &= \int R(u) \nabla_{\theta} p_\theta(u) \,\mathrm{d}u\\ &= \int R(u) \left(\frac{\nabla_{\theta} p_\theta(u)}{p_\theta(u)}\right) p_\theta(u) \,\mathrm{d}u\\ &= \int \left( R(u) \nabla_{\theta} \log p_\theta(u) \right) p_\theta(u)\,\mathrm{d}u \\ &= \mathbb{E}_{\theta}\left[ R(u) \nabla_{\theta} \log p_\theta(u) \right]\,. \end{align*} \]

因此，以下是用于最大化参数化分布的奖励的通用算法：

选择一些初始猜测 \(\theta_0\)

对 \(t\ge 1\) 迭代：

  • 从 \(p_{\theta_k}\) 中独立同分布地采样 \(u_k\)。
  • 设置 \(\theta_{k+1} = \theta_k + \alpha_k R(u_k) \nabla_{\theta} \log p_{\theta_k}(u_k)\)，其中 \(\alpha_k\) 是某个步长。

请注意，我们想要优化的奖励函数仅通过函数求值进行访问。我们不计算 \(R\) 本身的梯度。

因此，这种方法可以视为类似于随机搜索或 Nelder-Mead 的零阶优化算法。

让我们来看看这些想法如何在Flappy Bird游戏上发挥作用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
function reward = flappy_reward(states, actions)
    % Flappy bird游戏的奖励函数。
     % 输入: 
        % states: 2行k列矩阵，迄今为止的速度和高度
        % actions: k维行向量，迄今为止的加速度
    % 返回: 
        % reward: 实数，奖励值
        
    reward = 0.0;
    for i = 1:size(states, 2)
        state = states(:, i);
        action = actions(i);
        height = state(2);
        if height < 0
            reward = reward + (10 * height-10);
        end
        reward = reward - abs(action);
    end
end

function action = flappy_policy(theta, states, actions)
    % 策略函数
    % 输入: 
        % theta: 4维列向量，加权系数
        % states: 2行k列矩阵，迄今为止的速度和高度
        % actions: k维行向量，迄今为止的加速度（实际未使用）
    % 输出: 
        % action: 实数，动作完成后的加速度

        if size(states, 2) == 1
        states = [states, states];
    end
    state_vector = states(:,end-1:end); % 取最后两个状态
    action = theta' * reshape(state_vector, [], 1); %用theta进行加权
end

function reward = flappy_simulator(theta, num_steps)
    % 计算给定步数的策略奖励。
    % 输入: 
        % theta: 4维列向量，加权系数
        % num_steps: 仿真长度
    % 输出:
        % reward: 本轮仿真获得的奖励值
    policy = @(sts, ats) flappy_policy(theta, sts, ats);
    init_action = 0;
    init_state = [0;10];
    [states, actions] = unroll(@flappy_bird, init_state,init_action, policy, num_steps);
    reward = flappy_reward(states, actions);
end

然后定义优化的目标函数。注意「奖励值」是越大越好，但是我们的优化目标是求最小值，所以要加个负号：

1
2
3
function reward=objective(theta)
    reward=(-1.0)*flappy_simulator(theta,20);
end

进行仿真：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for i=1:9
    
    xs = random_search(@objective, zeros(4, 1), 10, @gss);
    
    % 创建策略函数
    policy = @(states, actions) flappy_policy(xs(:,end), states, actions);
    
    init_action = 0;
    init_state = [0;10];
    [states, actions] = unroll(@flappy_bird, init_state,init_action, policy, 20);
    
    heights = states(2,:);

    subplot(3,3,i);
    plot(1:length(heights), heights, 'LineWidth', 2);
    
    ylabel('height');
    xlabel('time');    
end

进行9次重复实验，结果如下：

如果将迭代次数增加为500次，结果如下：

技术
#Matlab #最优化
黑箱优化与强化学习（EEee227c Lecture20学习笔记）
https://suzumiyaakizuki.github.io/2024/12/13/黑箱优化与强化学习/
作者
SuzumiyaAkizuki
发布于
2024年12月13日
许可协议