本读书笔记阅读了相关资料 ,并且使用 Matlab 语言独立实现了其中的实验。
Matlab 语言要求所有函数都定义在代码的最后,但是为了阅读顺畅,本文档修改了部分代码的顺序。如果需要运行代码,请下载源代码文件 。
投影梯度下降
投影梯度下降(PGD)是一种解决带约束非线性优化问题的有力工具。它结合了梯度下降的直观性和投影操作的约束性,通过迭代地沿着负梯度方向更新解,并将更新后的解投影回可行域内,以确保解始终满足约束条件。
在无约束优化问题中,梯度下降法是一种常用的方法。然而,在实际应用中,许多问题都伴随着各种约束,如变量的界限、线性等式或不等式约束等。PGD通过在每一步中将梯度下降的结果投影回可行域,有效地处理这些约束。
PGD适用于目标函数\(f(x)\) 可微且定义在凸集 \(\Omega\) 上的问题。其基本步骤为:
计算当前点的梯度:\(\nabla f(x)\)
沿着负梯度方向更新:\(x_{k+1}’=x_k-\alpha_k\nabla f(x_k)\)
将\(x'\) 投影回可行域:\(x_{k+1}=P_{\Omega}(x'_{k+1})\)
PGD的基本函数形式为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 function xs = gradient_descent (init, steps, grad, proj) if nargin < 4 end for step = stepsend ) - step * grad(xs(:,end )));end end
热身:优化二次型
对于函数: \[
f(\boldsymbol{x})=\frac{1}{2}\|\boldsymbol{x}\|^2
\] 其梯度为: \[
\nabla f(\boldsymbol{x})=\boldsymbol{x}
\] 有:
1 2 3 4 5 6 7 function y = quadratic (x) 0.5 * (x' * x);end function grad = quadratic_gradient (x) end
注意到函数是1-光滑和1-强凸的。这意味着算法可以使用恒定的步长1来保证收敛。
1 2 3 x0 = randn (1000 ,1 ); 1.0 ], @quadratic_gradient);disp (all(xs(:,end )==0 ));
输出:
如果步长选取得有问题,那么会得到:
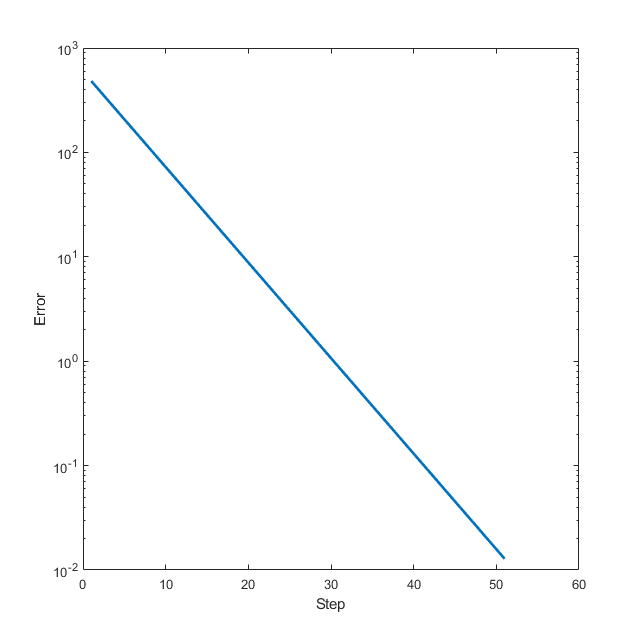
1 2 3 4 5 6 7 steps = 0.1 * ones (1 , 50 ); i ) quadratic(xs(:, i )), 1 :size (xs, 2 ));'log' );
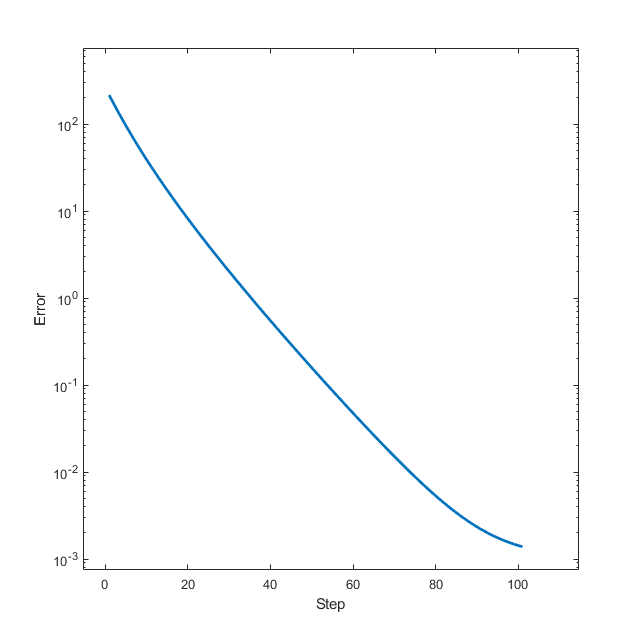
基本二次型
约束优化问题
如果我们把优化问题限制在一个仿射子空间中。注意到,仿射子空间是一个凸集,我们随机选取一个仿射子空间\(U+b\) ,并且定义投影函数:
1 2 3 4 5 6 7 U = randn (1000 , 100 ); randn (1000 ,1 ); function x_proj = proj1 (x,U,b) end
即: \[
P_{\Omega}(\boldsymbol{x})=UU^T(\boldsymbol{x-b})+\boldsymbol{b}
\] 进行优化仿真:
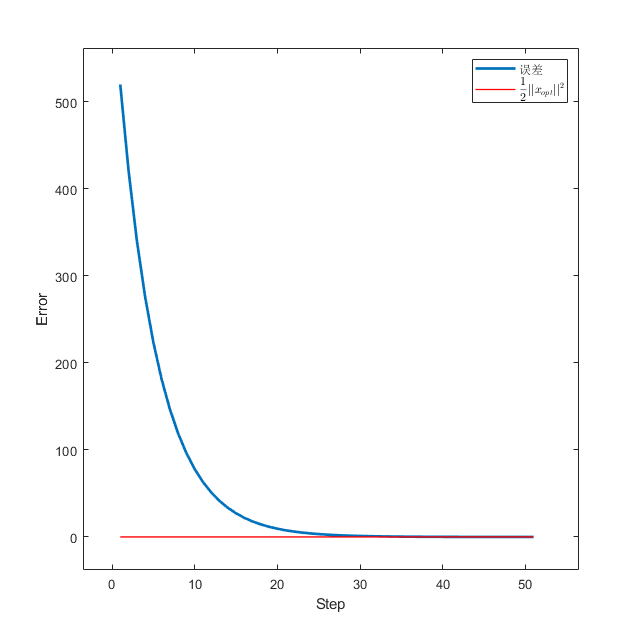
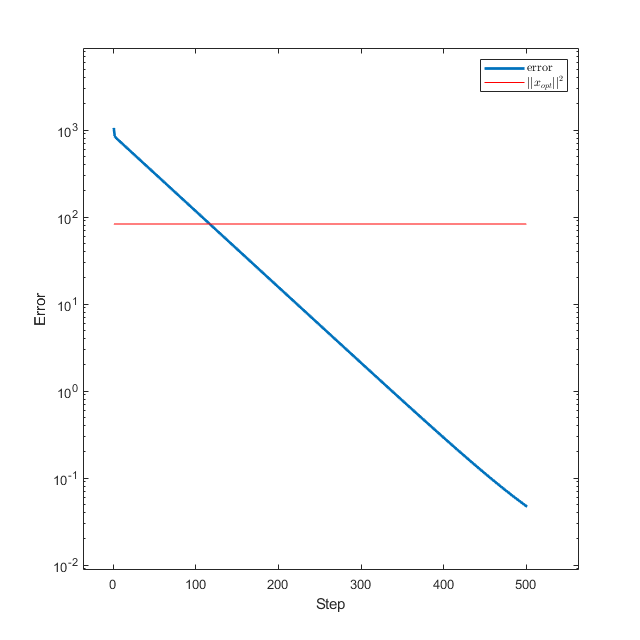
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 x0 = randn (1000 ,1 );0.1 * ones (1 , 50 );0 ,U,b); i ) quadratic(xs(:, i )), 1 :size (xs, 2 ));'linear' );hold on;ones (1 , size (xs,2 ));plot (1 :size (xs,2 ), quadratic_opt, 'r' , 'LineWidth' , 1 ); legend ('误差' ,'$$\frac{1}{2}||x_{opt}||^2$$' ); 'Interpreter' ,'latex' );hold off;
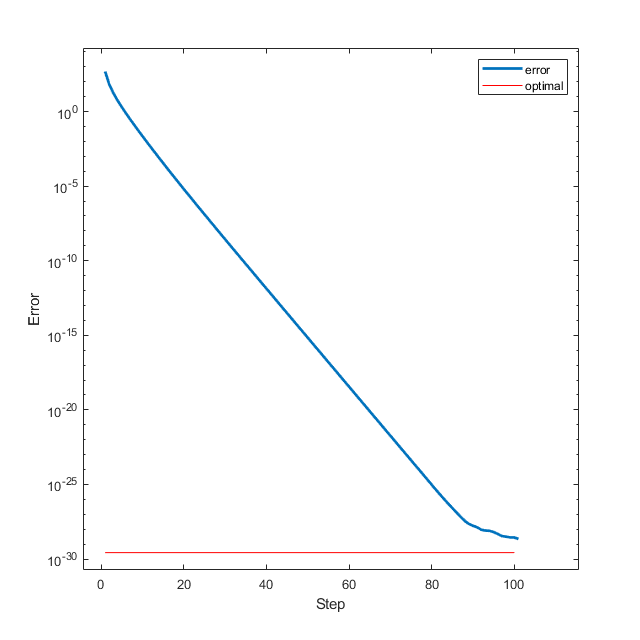
仿射空间约束优化
可以看到,算法在30步内就收敛到了很低的水平。我们还可以画一下迭代到的各点同最优解的距离,即\(k-\|x_k-x_{opt}\|^2\) 图像:
1 2 ys = arrayfun(@(i ) norm(xs(:, i )-x_opt)^2 , 1 :size (xs, 2 ));'log' );
我们称之为「领域收敛」。
最小二乘法
线性最小二乘法是数据分析中的重要工具,其目标是找到一个向量\(\boldsymbol{x}\) ,使得\(A\boldsymbol{x}-\boldsymbol{b}\) 的平方误差之和最小。问题的目标函数为: \[
f(\boldsymbol{x})=\frac 1{2m}\|A\boldsymbol{x}-\boldsymbol{b}\|^2
\] 它的梯度是: \[
\nabla f(\boldsymbol{x})=A^{T}(A\boldsymbol{x}-\boldsymbol{b})
\] 海森矩阵为: \[
\nabla^2f(\boldsymbol{x})=A^TA
\] 这个问题是\(\beta-\) 李普希兹的和\(\alpha-\) 强凸的,其中: \[
\beta=\lambda_\max(A^TA),\alpha=\lambda_{\min}(A^TA)
\] 定义目标函数和梯度:
1 2 3 4 5 6 7 8 9 function y = least_squares (A, b, x) size (A,1 );0.5 /m)*norm(A*x-b)^2 ;end function grad = least_squares_gradient (A, b, x) size (A,1 );end
过定问题:\(m>n\)
在这种情况下,最小二乘问题通常是有解的,而且目标函数是强凸的。为了仿真方便,我们先生成最优解,然后再用最优解加一个噪声反向生成问题中的\(b\) 。
1 2 3 4 5 6 7 8 9 10 11 12 1000 ;100 ;randn (m,n);randn (n,1 );randn (m,1 ) * 0.1 ;
进行仿真:
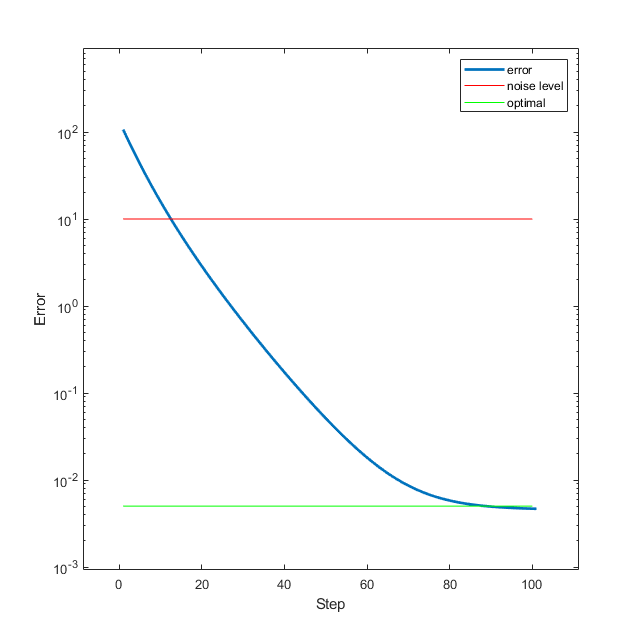
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 randn (n,1 );ones (1 ,100 )*0.1 ;i ) objective(xs(:, i )), 1 :size (xs, 2 ));'log' );hold on;2 *ones (1 ,100 );plot (1 :length (steps), noise_level,'r' );ones (1 ,100 );plot (1 :length (steps), optimal_level,'g' );legend ('error' , 'noise level' , 'optimal' );hold off;
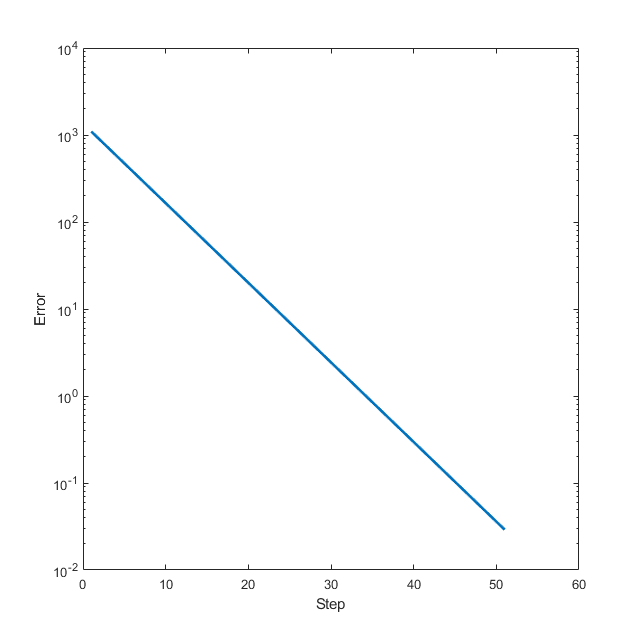
结果如下:
最小二乘-过定问题
我们还可以画一下迭代到的各点同最优解的距离,即\(k-\|x_k-x_{opt}\|^2\) 图像:
1 2 3 i ) norm(xs(:, i )-x_opt)^2 , 1 :size (xs, 2 ));'log' );
最小二乘-过定问题
欠定问题:\(m<n\)
在欠定时,目标函数可能不是强凸的,因为\(A^TA\) 不是满秩矩阵,而且\(\lambda_\min(A^TA)=0\) 。
运行仿真:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 100 ;1000 ;randn (m,n);randn (m,1 );randn (n,1 );ones (1 ,100 ) * 0.1 ;i ) objective(xs(:, i )), 1 :size (xs, 2 ));'log' );hold on;ones (1 ,100 );plot (1 :length (steps),optimal_level,'r' );legend ('error' , 'optimal' );hold off;
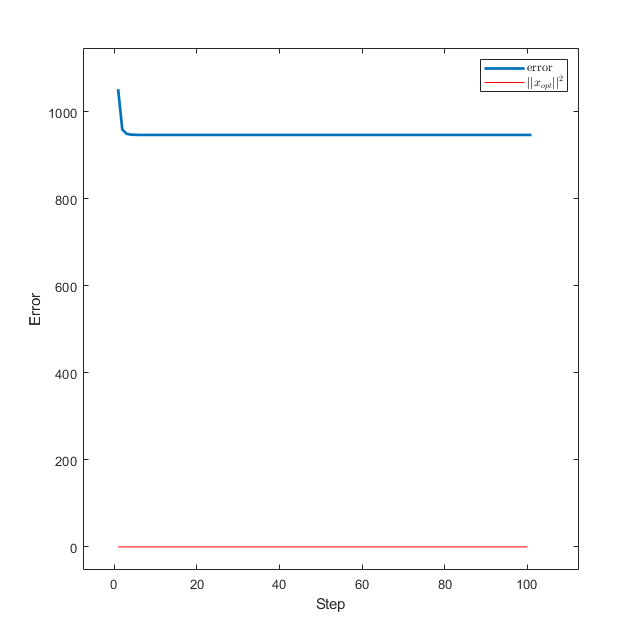
最小二乘:欠定问题
可以看到,算法并没有收敛到最优解。我们还可以画一下迭代到的各点同最优解的距离,即\(k-\|x_k-x_{opt}\|^2\) 图像:
1 2 3 4 5 6 7 8 i ) norm(xs(:, i )-x_opt)^2 , 1 :size (xs, 2 ));'linear' );hold on;2 *ones (1 ,100 );plot (1 :length (steps),optimal_norm,'r' );legend ('error' ,'$$||x_{opt}||^2$$' );'Interpreter' ,'latex' );
最小二乘:欠定问题
\(l_2-\) 正规化在之前讨论的欠定问题中,可以试图通过添加\(l_2-\) 罚函数来恢复问题的强凸性。
此时的目标函数变为: \[
f(\boldsymbol{x})=\frac 1{2m}\|A\boldsymbol{x}-\boldsymbol{b}\|+\frac \alpha 2\|\boldsymbol{x}\|^2
\] 这样一来,函数就是\(\alpha-\) 强凸的了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 function obj = least_squares_l2 (A, b, x, alpha) if nargin < 4 0.1 ; end 2 ) * x' * x;end function grad = least_squares_l2_gradient (A, b, x, alpha) if nargin < 4 0.1 ; end end
运行仿真:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 100 ;1000 ;randn (m,n);randn (n,1 );0.1 * eye (1000 )) * A' * b; randn (n,1 );ones (1 ,500 ) * 0.1 ;i ) objective(xs(:, i )), 1 :size (xs, 2 ));'log' );hold on;ones (1 ,500 );plot (1 :length (steps), optimal_level,'g' );legend ('error' , 'optimal' );hold off;
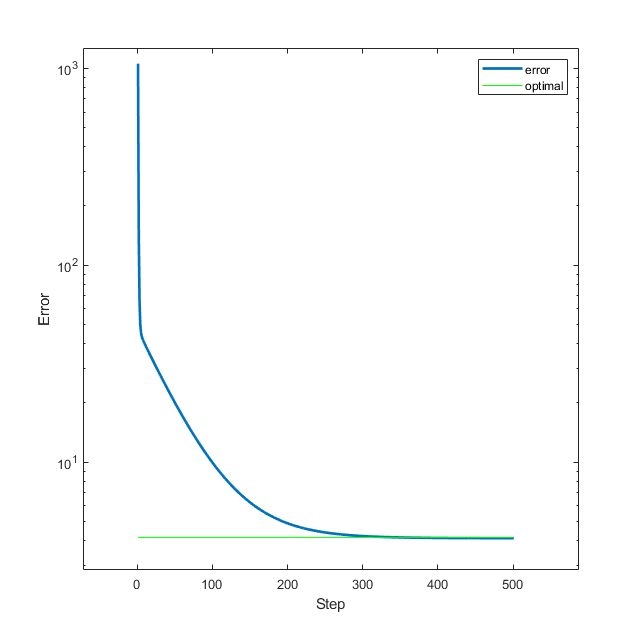
l2-正规化
由于正规化项的存在,函数并没有收敛到\(0\) ,但是这是正常的,至少它收敛了。事实上,正则化项具有很强的凸性,这将再次导致领域收敛:
1 2 3 4 5 6 7 8 i ) norm(xs(:, i )-x_opt)^2 , 1 :size (xs, 2 ));'log' );hold on;2 *ones (1 ,500 );plot (1 :length (steps),optimal_norm,'r' );legend ('error' ,'$$||x_{opt}||^2$$' );'Interpreter' ,'latex' );
l2-正规化
隐式正则化的魔力
有时,只需从一个合适的初始点开始梯度下降,本身就会产生正则化效果,而无需引入明确的正则化项。 我们将在下文中看到这一点,我们将重温非正则化最小二乘法目标,但从原点而非随机高斯点开始梯度下降。
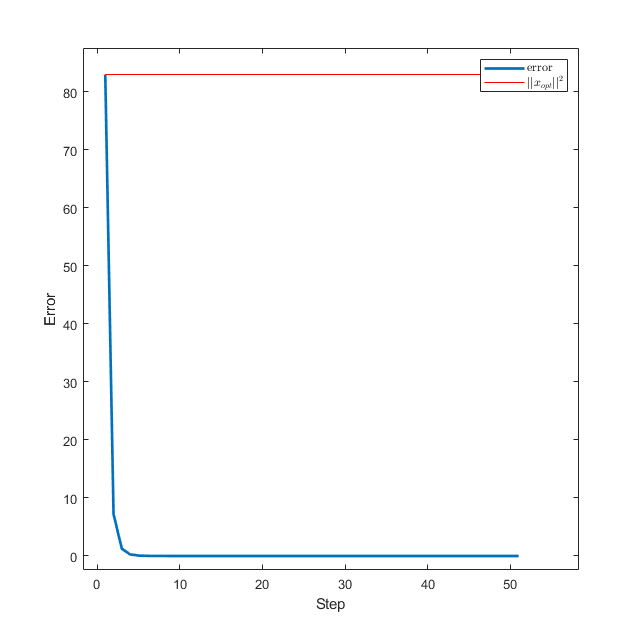
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 zeros (n,1 );ones (1 ,50 )*0.1 ;i ) norm(xs(:, i )-x_opt)^2 , 1 :size (xs, 2 ));'linear' );hold on;2 *ones (1 ,50 );plot (1 :length (steps),optimal_norm,'r' );legend ('error' ,'$$||x_{opt}||^2$$' );'Interpreter' ,'latex' );
隐式正则化
LASSO
回到之前的欠定问题。LASSO是\(l_1-\) 正则化最小二乘线性回归的名称。其目标函数为: \[
f(\boldsymbol{x})=\frac 1{2m}\|A\boldsymbol{x}-\boldsymbol{b}\|+\alpha \|\boldsymbol{x}\|_1
\]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 function obj = lasso (A, b, x, alpha) if nargin < 4 0.1 ; end 1 );end function g = ell1_subgradient (x) ones (size (x));0 ) = -1 ;end function subgrad = lasso_subgradient (A, b, x, alpha) if nargin < 4 0.1 ; end end
如果存在稀疏解,LASSO能够对其细化,这也是使用LASSO的重要原因之一。
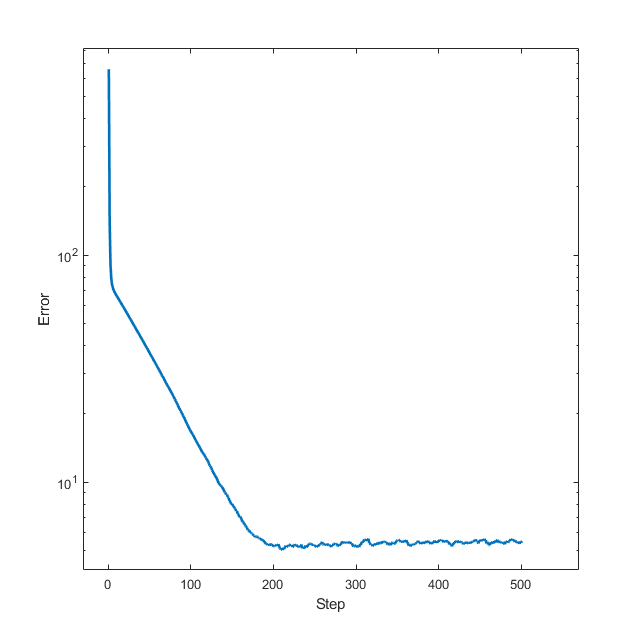
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 100 ;1000 ;randn (m,n);zeros (n,1 );1 :10 )=1 ; randn (n, 1 );0.1 * ones (1 , 500 ); i ) objective(xs(:, i )), 1 :size (xs, 2 ));'log' );
LASSO
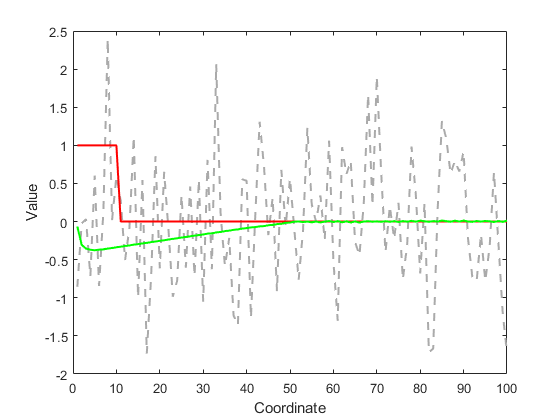
初始点、最佳点和计算点的比较:
1 2 3 4 5 6 7 8 9 1 :100 ; figure ;plot (idxs, x0(idxs), '--' , 'Color' , [0.6667 0.6667 0.6667 ], 'LineWidth' , 1.5 , 'DisplayName' , 'initial' );hold on;plot (idxs, x_opt(idxs), 'r-' , 'LineWidth' , 1.5 , 'DisplayName' , 'optimal' );plot (idxs, xs(end , idxs), 'g-' , 'LineWidth' , 1.5 , 'DisplayName' , 'final' ); 'Coordinate' );'Value' );
正如所承诺的那样,LASSO 能正确识别最优解的重要坐标。 因此,在实际应用中,LASSO 是一种常用的特征选择工具
支持向量机
在线性分类问题中,我们给出了 \(m\) 个标记点 \((a_i, y_i)\) ,我们希望找到一个由点 \(x\) 定义的超平面,将它们分开,使得:
当 \(y_i=1\) 时,\(\langle a_i, x\rangle \ge 1\) ;
当 \(y_i = -1\) 时,\(\langle a_i, x\rangle \le -1\) 。
范数 \(|x|\) 越小,正负实例之间的间隔就越大。因此,引入一个惩罚大范数的正则化项是有意义的。这导致了目标函数的产生。 \[
\frac 1m \sum_{i=1}^m \max\{1-y_i(a_i^\top x), 0\} + \frac{\alpha}2\|x\|^2
\]
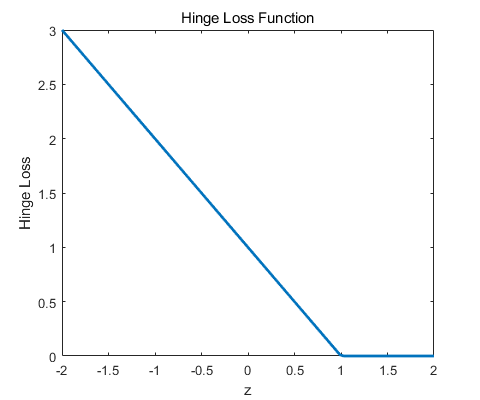
1 2 3 4 5 6 7 8 9 10 11 12 13 function loss = hinge_loss (z) max (1. -z, 0 );end function obj = svm_objective (A, y, x, alpha) if nargin < 4 0.1 ; end size (A, 1 ); mean (hinge_loss(diag (y) * (A * x))) + (alpha/2 ) * x' * x;end
绘制hinge_loss图像:
1 2 3 4 5 6 z = linspace (-2 , 2 , 100 );figure ('Position' , [100 , 100 , 480 , 400 ]); plot (z, hinge_loss(z), 'LineWidth' , 2 ); 'z' );'Hinge Loss' );'Hinge Loss Function' );
SVM
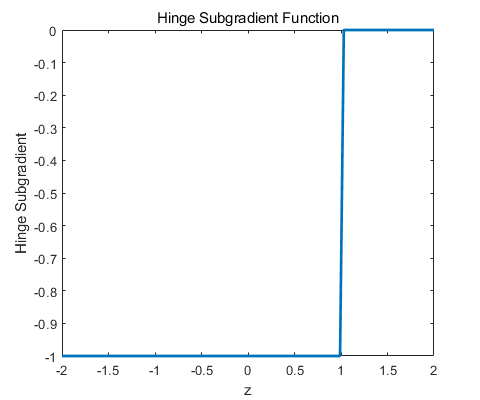
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 function g = hinge_subgradient (z) zeros (size (z));1 ) = -1 ;end function subgrad = svm_subgradient (A, y, x, alpha) if nargin < 4 0.1 ; end diag (y) * (A * x));diag (y) * A;end
绘制次梯度:
1 2 3 4 5 6 7 z = linspace (-2 , 2 , 100 );figure ('Position' , [100 , 100 , 480 , 400 ]);plot (z, hinge_subgradient(z), 'LineWidth' , 2 ); 'z' );'Hinge Subgradient' );'Hinge Subgradient Function' );
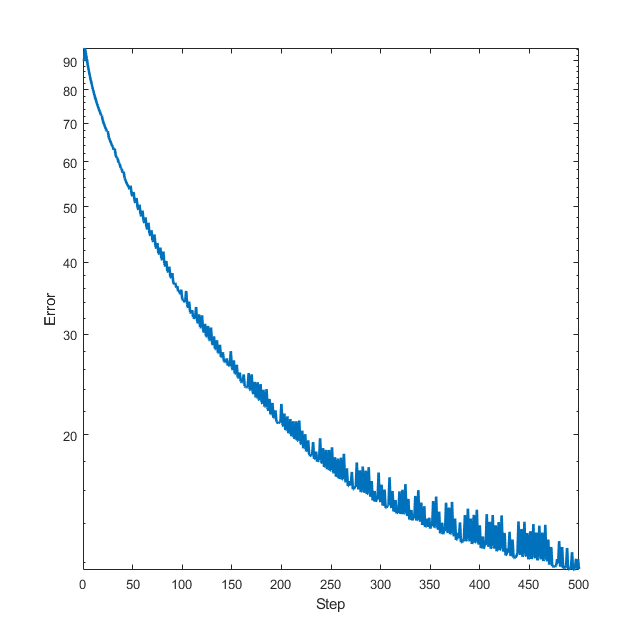
进行SVM仿真:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1000 ;100 ;randn (m/2 , n)*0.1 +randn (m/2 , n); -0.1 *randn (m/2 , n)+randn (m/2 , n)];ones (m/2 , 1 ); -1 *ones (m/2 , 1 )];randn (n, 1 );0.05 );0.05 );0.01 * ones (1 , 100 );i ) objective(xs(:, i )), 1 :size (xs, 2 ));'linear' );
让我们看看求解的平均值是否能带来更好的函数值。
1 2 3 4 5 6 7 8 xavg=0 ;for i = 1 :size (xs,2 )i );end size (xs,2 );disp ("Let's see if averaging out the solutions gives us an improved function value." );disp (objective(xs(:,end )));disp (objective(xavg));
输出:
1 2 3 4 Let's see if averaging out the solutions gives us an improved function value.
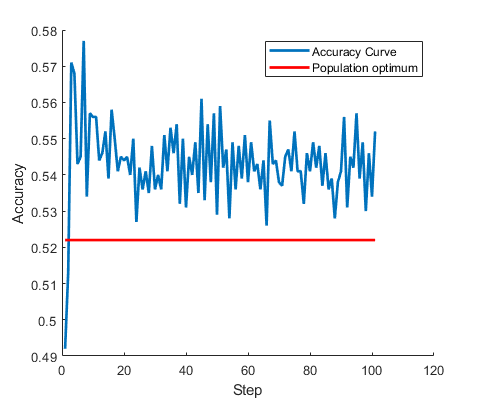
我们还可以看看线性模型预测标签的准确率。 从我们定义数据的方式可以看出,在无限数据(\(m\) 非常大)的情况下,全一向量是准确率最高的分类器。 对于有限数据集,由于随机波动,准确率可能会更高。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 function acc = accuracy (A, y, x) mean (diag (y) * (A * x) > 0 );end figure ('Position' , [100 , 100 , 480 , 400 ]); 'Accuracy' );'Step' );hold on; plot (1 :length (xs), arrayfun(@(i ) accuracy(A, y, xs(:,i )), 1 :size (xs,2 )), 'LineWidth' , 2 );plot (1 :length (xs), arrayfun(@(i ) accuracy(A, y, ones (n, 1 )),1 :size (xs,2 )), 'r' , 'LineWidth' , 2 , 'DisplayName' , 'Population optimum' );legend ('Accuracy Curve' , 'Population optimum' );
稀疏反协方差估计
稀疏逆协方差估计是一种统计方法,用于估计变量之间的依赖关系。该方法通过优化一个包含正则化项的目标函数来实现。其优化目标为: \[
\min _{X \in \mathbb{R}^{n \times n}, X \succeq 0}\langle S, X\rangle-\log \operatorname{det}(X)+\alpha\|X\|_1
\] 在这里,我们定义: \[
\langle S, X\rangle=\trace (S^\top X)
\] 和 \[
\|X\|_1=\sum_{ij}|X_{ij}|
\] 在原文中,使用到了python的autograd功能。但是Matlab不带有这个功能,为此,我颇下了一番功夫,最终得到一个解决方案。
这个问题解决起来很棘手,因为函数的参数都是矩阵。如果只用 syms A 指令,生成的只是单个变量。例如:
1 2 >> syms S Xlog (det(X)) + 0.1 * sum(abs (X),'all' )
输出
1 2 3 sparse_inv_cov_syms =abs (X)/10 - log (X) + X*conj (S)
这显然不是我们要的结果。这时,我们需要生成矩阵符号:
1 2 3 4 >> n=5 log (det(X)) + 0.1 * sum(abs (X),'all' )
输出
1 2 3 sparse_inv_cov_syms =abs (X1_1) 10 + abs (X1_2)/10 + abs (X1_3)/10 + abs (X1_4)/10 + abs (X1_5)/10 + abs (X2_1)/10 + ...
但是此时如果我们直接用MatlabFunction函数转换,会得到一个以25个变量为参数的函数:
1 >> ans =MatlabFunction(sparse_inv_cov_syms)
输出:
1 2 3 4 5 ans = @(S1_1,S1_2,S1_3,S1_4,S1_5,S2_1,S2_2,S2_3,S2_4,S2_5,S3_1,S3_2,S3_3,S3_4,S3_5,S4_1,S4_2,S4_3,S4_4,S4_5,S5_1,S5_2,S5_3,S5_4,S5_5,X1_1,X1_2,X1_3,X1_4,X1_5,X2_1,X2_2,X2_3,X2_4,X2_5,X3_1,X3_2,X3_3,X3_4,X3_5,X4_1,X4_2,X4_3,X4_4,X4_5,X5_1,X5_2,X5_3,X5_4,X5_5 )...
这并不是我们需要的形式。在生成函数时,我们使用Vars字符串,然后把S和X用大括号括起来,这样就行了。
1 >> ans =MatlabFunction(sparse_inv_cov_syms,"Vars" ,{S,X})
输出
1 2 3 4 5 ans = @(in1,in2 )abs(in2(1 )./1.0e+1 +abs(in2(6 )./1.0e+1 +abs(in2(11 )./1.0e+1 +abs(in2(16 )./1.0e+1 +abs(in2(21 )./1.0e+1 +abs(in2(2 )./1.0e+1 +abs(in2(7 )./1.0e+1 +abs(in2(12 )./1.0e+1 +abs(in2(17 )./1.0e+1 +abs(in2(22 )./1.0e+1 +abs(in2(3 )./1.0e+1 +abs(in2(8 )./1.0e+1 +abs(in2(13 )./1.0e+1 +abs(in2(18 )./1.0e+1 +abs(in2(23 )./1.0e+1 +abs(in2(4 )./1.0e+1 +abs(in2(9 )./1.0e+1 +abs(in2(14 )./1.0e+1 +abs(in2(19 )./1.0e+1 +abs(in2(24 )./1.0e+1 +abs(in2(5 )./1.0e+1 +abs(in2(10 )./1.0e+1 +abs(in2(15 )./1.0e+1 +abs(in2(20 )./1.0e+1 +abs(in2(25 )./1.0e+1 -log(in2(1 7 13 19 25 1 7 13 24 20 1 7 18 14 25 1 7 18 24 15 1 7 23 14 20 1 7 23 19 15 1 12 8 19 25 1 12 8 24 20 1 12 18 9 25 1 12 18 24 10 1 12 23 9 20 1 12 23 19 10 1 17 8 14 25 1 17 8 24 15 1 17 13 9 25 1 17 13 24 10 1 17 23 9 15 1 17 23 14 10 1 22 8 14 20 1 22 8 19 15 1 22 13 9 20 1 22 13 19 10 1 22 18 9 15 1 22 18 14 10 6 2 13 19 25 6 2 13 24 20 6 2 18 14 25 6 2 18 24 15 6 2 23 14 20 6 2 23 19 15 6 12 3 19 25 6 12 3 24 20 6 12 18 4 25 6 12 18 24 5 6 12 23 4 20 6 12 23 19 5 6 17 3 14 25 6 17 3 24 15 6 17 13 4 25 6 17 13 24 5 6 17 23 4 15 6 17 23 14 5 6 22 3 14 20 6 22 3 19 15 6 22 13 4 20 6 22 13 19 5 6 22 18 4 15 6 22 18 14 5 11 2 8 19 25 11 2 8 24 20 11 2 18 9 25 11 2 18 24 10 11 2 23 9 20 11 2 23 19 10 11 7 3 19 25 11 7 3 24 20 11 7 18 4 25 11 7 18 24 5 11 7 23 4 20 11 7 23 19 5 11 17 3 9 25 11 17 3 24 10 11 17 8 4 25 11 17 8 24 5 11 17 23 4 10 11 17 23 9 5 11 22 3 9 20 11 22 3 19 10 11 22 8 4 20 11 22 8 19 5 11 22 18 4 10 11 22 18 9 5 16 2 8 14 25 16 2 8 24 15 16 2 13 9 25 16 2 13 24 10 16 2 23 9 15 16 2 23 14 10 16 7 3 14 25 16 7 3 24 15 16 7 13 4 25 16 7 13 24 5 16 7 23 4 15 16 7 23 14 5 16 12 3 9 25 16 12 3 24 10 16 12 8 4 25 16 12 8 24 5 16 12 23 4 10 16 12 23 9 5 16 22 3 9 15 16 22 3 14 10 16 22 8 4 15 16 22 8 14 5 16 22 13 4 10 16 22 13 9 5 21 2 8 14 20 21 2 8 19 15 21 2 13 9 20 21 2 13 19 10 21 2 18 9 15 21 2 18 14 10 21 7 3 14 20 21 7 3 19 15 21 7 13 4 20 21 7 13 19 5 21 7 18 4 15 21 7 18 14 5 21 12 3 9 20 21 12 3 19 10 21 12 8 4 20 21 12 8 19 5 21 12 18 4 10 21 12 18 9 5 21 17 3 9 15 21 17 3 14 10 21 17 8 4 15 21 17 8 14 5 21 17 13 4 10 21 17 13 9 5 )+in2(1 in1(1 )+in2(6 in1(6 )+in2(11 in1(11 )+in2(16 in1(16 )+in2(21 in1(21 )+in2(2 in1(2 )+in2(7 in1(7 )+in2(12 in1(12 )+in2(17 in1(17 )+in2(22 in1(22 )+in2(3 in1(3 )+in2(8 in1(8 )+in2(13 in1(13 )+in2(18 in1(18 )+in2(23 in1(23 )+in2(4 in1(4 )+in2(9 in1(9 )+in2(14 in1(14 )+in2(19 in1(19 )+in2(24 in1(24 )+in2(5 in1(5 )+in2(10 in1(10 )+in2(15 in1(15 )+in2(20 in1(20 )+in2(25 in1(25 )
此时如果想用gradient函数求微分,又会报错:
1 >> g = gradient(sparse_inv_cov_syms,Xsyms)
输出:
1 2 错误使用 sym/gradient (line 39 )argument must be a vector of variables.
既然他说 must be a vector,那就把它向量化:
1 2 >> Xvec=X(:)
输出:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 g =conj (Ssyms1_1) + sign (Xsyms1_1)/10 - (Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms2_1) + sign (Xsyms2_1)/10 + (Xsyms1_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms3_4*Xsyms4_3*Xsyms5_2)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms3_1) + sign (Xsyms3_1)/10 - (Xsyms1_2*Xsyms2_3*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_4*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_5*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms4_4*Xsyms5_3 - Xsyms1_3*Xsyms2_2*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_4*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_5*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms4_4*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_3*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_5*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_3*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_4*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms4_3*Xsyms5_2)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms4_1) + sign (Xsyms4_1)/10 + (Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms5_4 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms5_3 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms5_3 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms5_4 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms5_2 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms5_3 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms5_2 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms5_3 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms5_2 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms5_2)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms5_1) + sign (Xsyms5_1)/10 - (Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms1_2) + sign (Xsyms1_2)/10 + (Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms2_2) + sign (Xsyms2_2)/10 - (Xsyms1_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms3_4*Xsyms4_3*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms3_2) + sign (Xsyms3_2)/10 + (Xsyms1_1*Xsyms2_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms4_4*Xsyms5_3 - Xsyms1_3*Xsyms2_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms4_4*Xsyms5_1 + Xsyms1_4*Xsyms2_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms4_3*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms4_2) + sign (Xsyms4_2)/10 - (Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms5_4 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms5_3 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms5_4 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms5_1 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms5_3 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms5_1 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms5_3 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms5_2) + sign (Xsyms5_2)/10 + (Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms1_3) + sign (Xsyms1_3)/10 - (Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms2_3) + sign (Xsyms2_3)/10 + (Xsyms1_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms3_4*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms3_3) + sign (Xsyms3_3)/10 - (Xsyms1_1*Xsyms2_2*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_4*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_5*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms4_4*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_4*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_5*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms4_4*Xsyms5_1 + Xsyms1_4*Xsyms2_1*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_2*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_1*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_2*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms4_3) + sign (Xsyms4_3)/10 + (Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms5_4 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms5_2 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms5_4 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms5_1 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms5_1 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms5_2 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms5_1 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms5_2 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms5_3) + sign (Xsyms5_3)/10 - (Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms1_4) + sign (Xsyms1_4)/10 + (Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms2_4) + sign (Xsyms2_4)/10 - (Xsyms1_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms3_3*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms3_4) + sign (Xsyms3_4)/10 + (Xsyms1_1*Xsyms2_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_5*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_5*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_5*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_3*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms4_4) + sign (Xsyms4_4)/10 - (Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms5_2 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms5_3 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms5_1 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms5_3 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms5_1 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms5_2 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms5_1 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms5_3 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms5_2 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms5_3 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms5_1 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms5_2 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms5_4) + sign (Xsyms5_4)/10 + (Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms1_5) + sign (Xsyms1_5)/10 - (Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms2_5) + sign (Xsyms2_5)/10 + (Xsyms1_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms3_5) + sign (Xsyms3_5)/10 - (Xsyms1_1*Xsyms2_2*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms4_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms4_5) + sign (Xsyms4_5)/10 + (Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms5_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)conj (Ssyms5_5) + sign (Xsyms5_5)/10 - (Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1)/(Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_5 - Xsyms1_1*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_5 + Xsyms1_1*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_3 + Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_4 - Xsyms1_1*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_3 - Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_5 + Xsyms1_1*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_5 - Xsyms1_1*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_2 - Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_4 + Xsyms1_1*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_5 - Xsyms1_1*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_5 + Xsyms1_1*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_2 + Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_3 - Xsyms1_1*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_4 + Xsyms1_1*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_4 - Xsyms1_1*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_2 - Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_3 + Xsyms1_1*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_5 + Xsyms1_2*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_5 - Xsyms1_2*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_3 - Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_4 + Xsyms1_2*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_3 + Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_5 - Xsyms1_2*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_5 + Xsyms1_2*Xsyms2_3*Xsyms3_4*Xsyms4_5*Xsyms5_1 + Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_4 - Xsyms1_2*Xsyms2_3*Xsyms3_5*Xsyms4_4*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_5 + Xsyms1_2*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_5 - Xsyms1_2*Xsyms2_4*Xsyms3_3*Xsyms4_5*Xsyms5_1 - Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_3 + Xsyms1_2*Xsyms2_4*Xsyms3_5*Xsyms4_3*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_4 - Xsyms1_2*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_4 + Xsyms1_2*Xsyms2_5*Xsyms3_3*Xsyms4_4*Xsyms5_1 + Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_3 - Xsyms1_2*Xsyms2_5*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_5 - Xsyms1_3*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_5 + Xsyms1_3*Xsyms2_1*Xsyms3_4*Xsyms4_5*Xsyms5_2 + Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_4 - Xsyms1_3*Xsyms2_1*Xsyms3_5*Xsyms4_4*Xsyms5_2 - Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_5 + Xsyms1_3*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_5 - Xsyms1_3*Xsyms2_2*Xsyms3_4*Xsyms4_5*Xsyms5_1 - Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_4 + Xsyms1_3*Xsyms2_2*Xsyms3_5*Xsyms4_4*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_5 - Xsyms1_3*Xsyms2_4*Xsyms3_1*Xsyms4_5*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_5 + Xsyms1_3*Xsyms2_4*Xsyms3_2*Xsyms4_5*Xsyms5_1 + Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_1*Xsyms5_2 - Xsyms1_3*Xsyms2_4*Xsyms3_5*Xsyms4_2*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_4 + Xsyms1_3*Xsyms2_5*Xsyms3_1*Xsyms4_4*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_4 - Xsyms1_3*Xsyms2_5*Xsyms3_2*Xsyms4_4*Xsyms5_1 - Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_1*Xsyms5_2 + Xsyms1_3*Xsyms2_5*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_5 + Xsyms1_4*Xsyms2_1*Xsyms3_2*Xsyms4_5*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_5 - Xsyms1_4*Xsyms2_1*Xsyms3_3*Xsyms4_5*Xsyms5_2 - Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_2*Xsyms5_3 + Xsyms1_4*Xsyms2_1*Xsyms3_5*Xsyms4_3*Xsyms5_2 + Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_5 - Xsyms1_4*Xsyms2_2*Xsyms3_1*Xsyms4_5*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_5 + Xsyms1_4*Xsyms2_2*Xsyms3_3*Xsyms4_5*Xsyms5_1 + Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_1*Xsyms5_3 - Xsyms1_4*Xsyms2_2*Xsyms3_5*Xsyms4_3*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_5 + Xsyms1_4*Xsyms2_3*Xsyms3_1*Xsyms4_5*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_5 - Xsyms1_4*Xsyms2_3*Xsyms3_2*Xsyms4_5*Xsyms5_1 - Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_1*Xsyms5_2 + Xsyms1_4*Xsyms2_3*Xsyms3_5*Xsyms4_2*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_2*Xsyms5_3 - Xsyms1_4*Xsyms2_5*Xsyms3_1*Xsyms4_3*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_1*Xsyms5_3 + Xsyms1_4*Xsyms2_5*Xsyms3_2*Xsyms4_3*Xsyms5_1 + Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_1*Xsyms5_2 - Xsyms1_4*Xsyms2_5*Xsyms3_3*Xsyms4_2*Xsyms5_1 + Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_3*Xsyms5_4 - Xsyms1_5*Xsyms2_1*Xsyms3_2*Xsyms4_4*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_2*Xsyms5_4 + Xsyms1_5*Xsyms2_1*Xsyms3_3*Xsyms4_4*Xsyms5_2 + Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_2*Xsyms5_3 - Xsyms1_5*Xsyms2_1*Xsyms3_4*Xsyms4_3*Xsyms5_2 - Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_3*Xsyms5_4 + Xsyms1_5*Xsyms2_2*Xsyms3_1*Xsyms4_4*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_1*Xsyms5_4 - Xsyms1_5*Xsyms2_2*Xsyms3_3*Xsyms4_4*Xsyms5_1 - Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_1*Xsyms5_3 + Xsyms1_5*Xsyms2_2*Xsyms3_4*Xsyms4_3*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_2*Xsyms5_4 - Xsyms1_5*Xsyms2_3*Xsyms3_1*Xsyms4_4*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_1*Xsyms5_4 + Xsyms1_5*Xsyms2_3*Xsyms3_2*Xsyms4_4*Xsyms5_1 + Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_1*Xsyms5_2 - Xsyms1_5*Xsyms2_3*Xsyms3_4*Xsyms4_2*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_2*Xsyms5_3 + Xsyms1_5*Xsyms2_4*Xsyms3_1*Xsyms4_3*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_1*Xsyms5_3 - Xsyms1_5*Xsyms2_4*Xsyms3_2*Xsyms4_3*Xsyms5_1 - Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_1*Xsyms5_2 + Xsyms1_5*Xsyms2_4*Xsyms3_3*Xsyms4_2*Xsyms5_1)
成功了。
所以我先用Matlab的符号运算生成了矩阵符号,书写函数以后,将被求导的矩阵转换成向量,用gradient函数进行符号求导,然后再进行一次矩阵向量化的包装,这样一来,基本可以实现autograd自动求导的效果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 5 ;randn (n,n);5 ; 5 ;log (det(Xsyms)) + 0.1 * sum(abs (Xsyms),'all' ); "Vars" ,{Ssyms,Xsyms}); "Vars" ,{Ssyms,X_vec});
定义投影函数:
1 2 3 4 5 6 function X_proj = projection (X) 0 ) = 0 ;end
因为这里的优化目标\(X\) 也是矩阵,所以梯度下降函数的写法也做了相应修改:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 function xs = gradient_descent_xx (n,init, steps, grad, proj) if nargin < 5 end for step = stepssize (xs, 2 ) - n) + 1 ; size (xs ,2 ); reshape (G,size (lastSubMatrix));end end
运行仿真:
1 2 3 4 5 6 7 8 A0 = randn (n,n);ones (1 ,500 )*0.01 ;i ) objective(S,Xs(:,(i -1 )*n+1 :i *n)), 1 :500 );'log' );
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏: