合成孔径雷达的「斑马图」到底是怎么回事
在合成孔径雷达(以下简称SAR)的波位设计中,经常会遇到一个叫做「斑马图」(或者「菱形图」)的东西,它大概长这样:
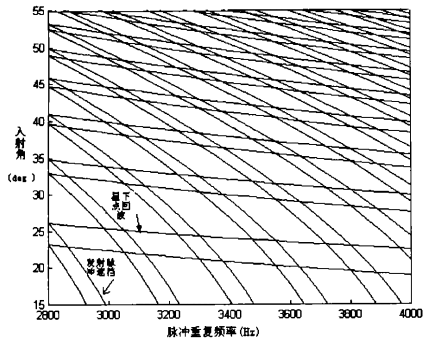
斑马图的横轴是脉冲重复频率,纵轴一般是入射角或者距星下点地面距离。其中有两组曲线,分别表示了星下点回波的干扰和发射信号盲区。对于发射和接收公用一个天线的星载 SAR 系统,由于在任何时刻空中同时有发射脉冲、星下点脉冲和回波必须对 PRF 加以限制,使发射脉冲、星下点脉冲不落在回波窗之中。只有当脉冲重复频率和星下点地面距离的选择在图里的「大菱形区域」里,SAR才能正常工作。如何选择脉冲重复频率或者星下点地面距离,就是所谓的「波位设计」。
我接触到的很多教材都对这个东西的绘制语焉不详,所以在这里我写一下怎么画。画斑马图的关键是几何关系:
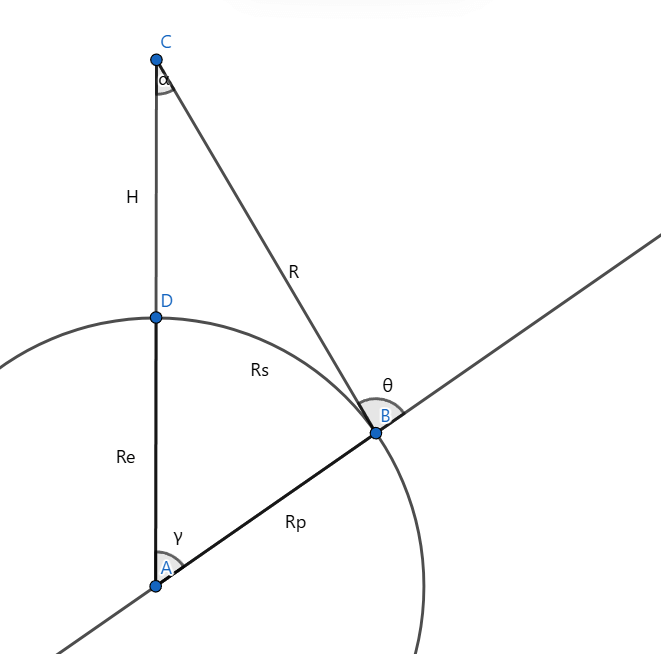
在这个图中,以点\(A\)为圆心的圆形表示地球,点\(C\)表示SAR卫星,点\(B\)表示目标,点\(D\)表示SAR卫星和地心的连线,也就是星下点。其它长度和角度的名称如下:
- \(R_e\):即线段\(DA\)的长度,地球半径,已知
- \(R_p\):即线段\(BA\)的长度,也是地球半径,已知
- \(R_s\):圆弧\(DB\)的长度,地距
- \(R\):线段\(CB\)的长度,斜距
- \(H\):线段\(CD\)的长度,卫星高度,已知
- \(\alpha\):\(\angle DCB\),视角
- \(\theta\):\(\pi-\angle{CBA}\),入射角
- \(\gamma\):\(\angle{DAB}\),地心角,显然有:\(\gamma=\theta-\alpha\)
对于一个SAR系统,要绘制其斑马图,还要知道脉冲宽度\(\tau\)、斑马图横坐标的范围(最大最小脉冲重复频率)、最大最小中心视角。
绘制发射信号干扰带的斑马图
计算其前后沿回波时间:
假设总共要画\(m\)个曲线,现在正在画第\(j\)个,当前正在看的脉冲重复频率为\(f_{PRF}\),有 \[ \begin{align} T_{e_1}=\frac{j}{f_{PRF}}-(\tau+T_g)\\\\ T_{e_1}=\frac{j}{f_{PRF}}+(\tau+T_g) \end{align} \] 这里面的\(T_g\)叫做「保护时间带」,我还不太确定这是什么,好像是一种类似于冗余的东西,取\(0\)也没关系。
计算对应的最大最小斜距: \[ \begin{align} R_{\min}=T_{e_1}\frac c2=\left(\frac{j}{f_{PRF}}-(\tau+T_g)\right)\cdot\frac c2\\\\ R_{\max}=T_{e_2}\frac c2=\left(\frac{j}{f_{PRF}}+(\tau+T_g)\right)\cdot\frac c2 \end{align} \]
计算对应的最大最小视角:
即解三角形\(CBA\),对\(\alpha\)应用余弦定理: \[ \alpha=\arccos\left(\frac{R^2+(R_e+H)^2-R_p^2}{2R(R_e+H)}\right) \] 有: \[ \begin{align} \alpha_{\max}=\arccos\left(\frac{R_\max^2+(R_e+H)^2-R_p^2}{2R_\max(R_e+H)}\right)\\\\ \alpha_{\min}=\arccos\left(\frac{R_\min^2+(R_e+H)^2-R_p^2}{2R_\min(R_e+H)}\right) \end{align} \]
计算对应的最大最小入射角:
即解三角形\(CBA\),求解\(\theta\)。
由余弦定理: \[ \angle CBA=\arccos\left(\frac{R_p^2+R^2-(R_e+H)^2}{2R_pR}\right) \] 有: \[ \begin{align} \theta_{\max}=\pi-\arccos\left(\frac{R_p^2+R_{\max}^2-(R_e+H)^2}{2R_pR_{\max}}\right)\\\\ \theta_{\min}=\pi-\arccos\left(\frac{R_p^2+R_{\min}^2-(R_e+H)^2}{2R_pR_{\min}}\right) \end{align} \]
计算最大最小地距:
由圆弧\(DB\),得:\(R_s=\gamma R_e=(\theta-\alpha)R_e\)。有: \[ \begin{align} R_{s_\max}=(\theta_\max-\alpha_\max)R_e\\\\ R_{s_\min}=(\theta_\min-\alpha_\min)R_e \end{align} \]
由上面的推导,可以看出,\(R_{s\min}\)和\(R_{s\max}\)总的来说是\(j\)和\(f_{PRF}\)的函数。在计算时,我们写一个双重循环,外层循环遍历\(f_{PRF}\),内层循环遍历\(j\),然后算出\(R_{s\max},R_{s\min}\)并画图就行了。
让我们说得再明白一点,也就是说每个\(j\)对应两条曲线:\(R_{s\max}(f_{PRF}),R_{s\min}(f_{PRF})\)。
现在的问题是:\(j\)怎么取值?首先明确\(j\)是正整数。如果\(j\)取得太小,会让三角形无解(表现为\(\arccos\)函数算出来不是实数)。如果\(j\)取得太大,会让画出来的曲线没有意义(在图上不显示)。书上说: \[ \begin{align} j_{\min}=\lfloor{T_{e\min}\cdot f_{PRF\min}}\rfloor\\\\ j_{\max}=\lfloor{T_{e\max}\cdot f_{PRF\max}}\rfloor \end{align} \] 其中,\(T_e\)是所选择区域的最近/远斜距对应的回波时间,\(f_{PRF}\)是所选择的最小/大可能脉冲重复频率。在这里,\(f_{PRF}\)的最大最小值很容易理解,已经被给定了。但是\(T_e\)需要计算,因为给定的是最小/大中心视角。
回到前面的几何关系:

也就是说,解三角形\(CBA\),给定\(CA,AB,\alpha\),求解\(CB\)。注意在数学里这个三角形似乎并不唯一确定(有两个解),但是在我们这里显然只需要取\(\angle CBA\)是钝角的那个解。
过\(A\)作直线\(CB\)的垂线交于点\(E\):
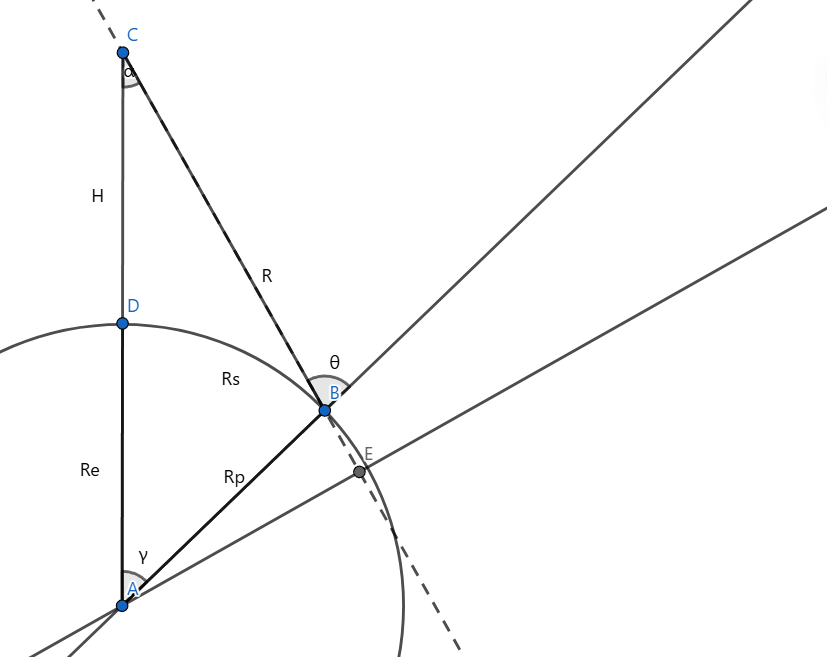
则有: \[ AE=(Re+H)\sin\alpha \]
于是 \[ \angle BAE=\arccos\left(\frac{AE}{R_p}\right)=\arccos\left(\frac{(Re+H)\sin\alpha}{R_p}\right) \] 则 \[ \gamma=\frac \pi2-\alpha-\angle BAE=\frac \pi2-\alpha-\arccos\left(\frac{(Re+H)\sin\alpha}{R_p}\right) \] 由正弦定理 \[ \frac{R_p}{\sin \alpha}=\frac{R}{\sin \gamma} \] 有 \[ R=\frac{\sin \gamma R_p}{\sin \alpha} \] 则 \[ T_e=\frac {2R}{c} \] 其中\(c\)是光速。这样一来,我们就把\(T_e\)表示成了\(\alpha\)的函数: \[ T_e=\frac {2}{c} \frac{\sin\left(\frac \pi2-\alpha-\arccos\left(\frac{(Re+H)\sin\alpha}{R_p}\right)\right)R_p}{\sin \alpha} \]
绘制星下点回波区的斑马图
首先,计算前后沿回波时间 \[ \begin{align} T_\min=\frac {2h}c+\frac i {f_{PRF}}-(\tau+T_g)\\\\ T_\max=\frac {2h}c+\frac i {f_{PRF}}+(\tau+T_g) \end{align} \]
后面的计算和上一部分的完全一样。
关于\(i\)的取值,有: \[ \begin{align} i_\min&=j_\min-\lfloor (T_{nad}+\tau+2T_g)f_{PRF\min}\rfloor\\\\ i_\max&=j_\max-\lfloor T_{nad}f_{PRF\min}\rfloor \end{align} \] 其中 \[ T_{nad}=\frac{2h}c-T_g \] 称为「星下点回波起始时间」。
算法伪代码


本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
