通信原理Matlab软件作业

《通信原理》课程的实践部分包含了四次Matlab作业，两个Matlab仿真实验和两个上电路板的虚拟仿真实验。涉及到Matlab编程的部分在下面，虚拟仿真实验的文件和报告在全文最后供下载。

Matlab作业一：线性调制

(同上机实验一)

分别用计算机仿真AM、DSB、SSB模拟调制、解调过程，其中，调制信号（基带信号）\(m(t)=\cos 2\pi f_mt\)。调制信号与载波频率自定，要求调制信号频率远小于载波频率。信号时长为8个调制信号周期。

输出结果包括：

  1. 输入信号波形；

  2. 载波波形；

  3. 已调信号波形及其包络；

  4. 已调信号功率谱；

  5. 相干解调下变频之后、低通滤波之前的信号波形；

  6. 相干解调低通滤波之后的信号波形。

实验结果

AM调制

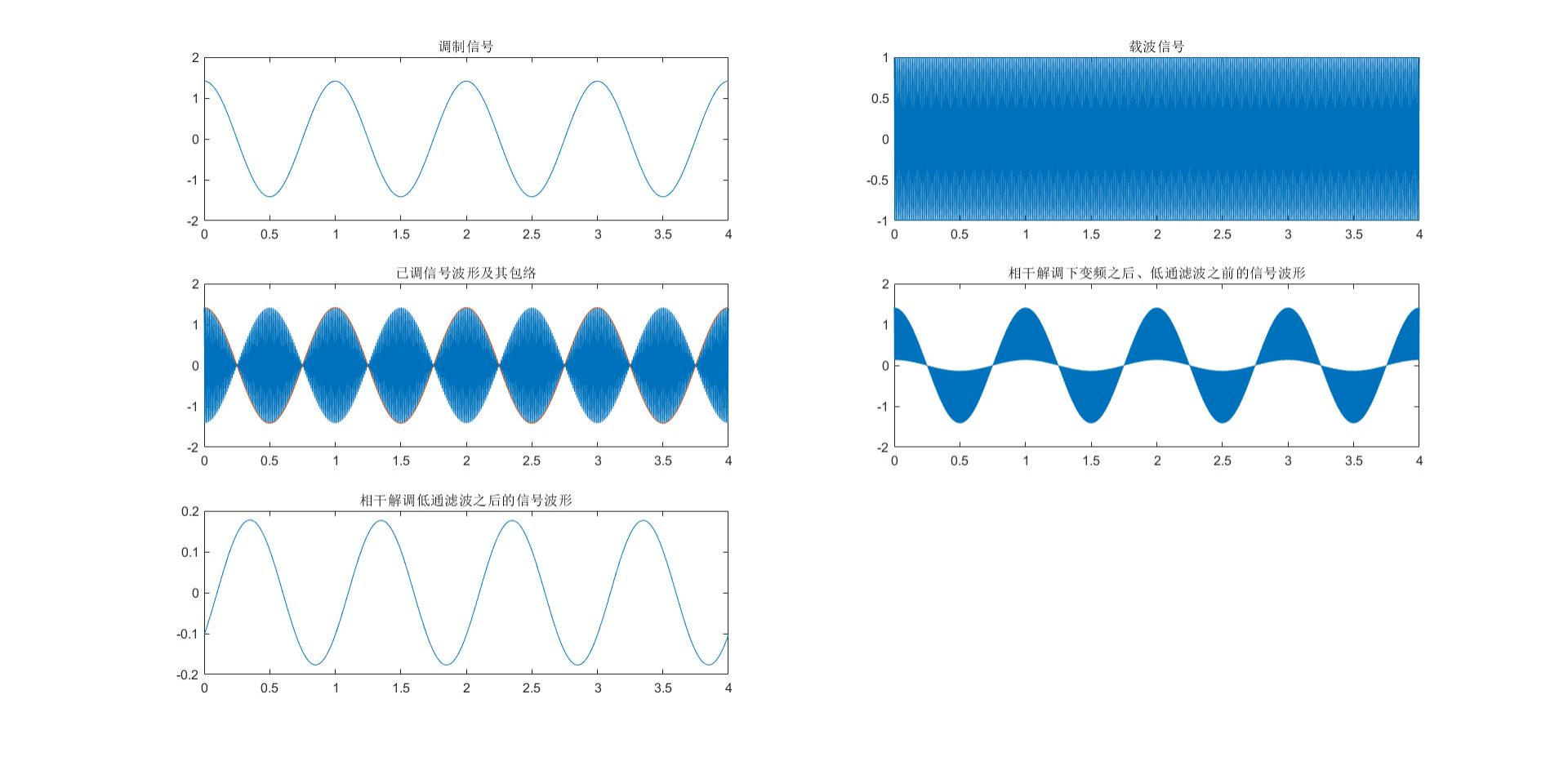
AM调制相关的图像如上所示。已调信号的包络完全反映了调制信号的波形。

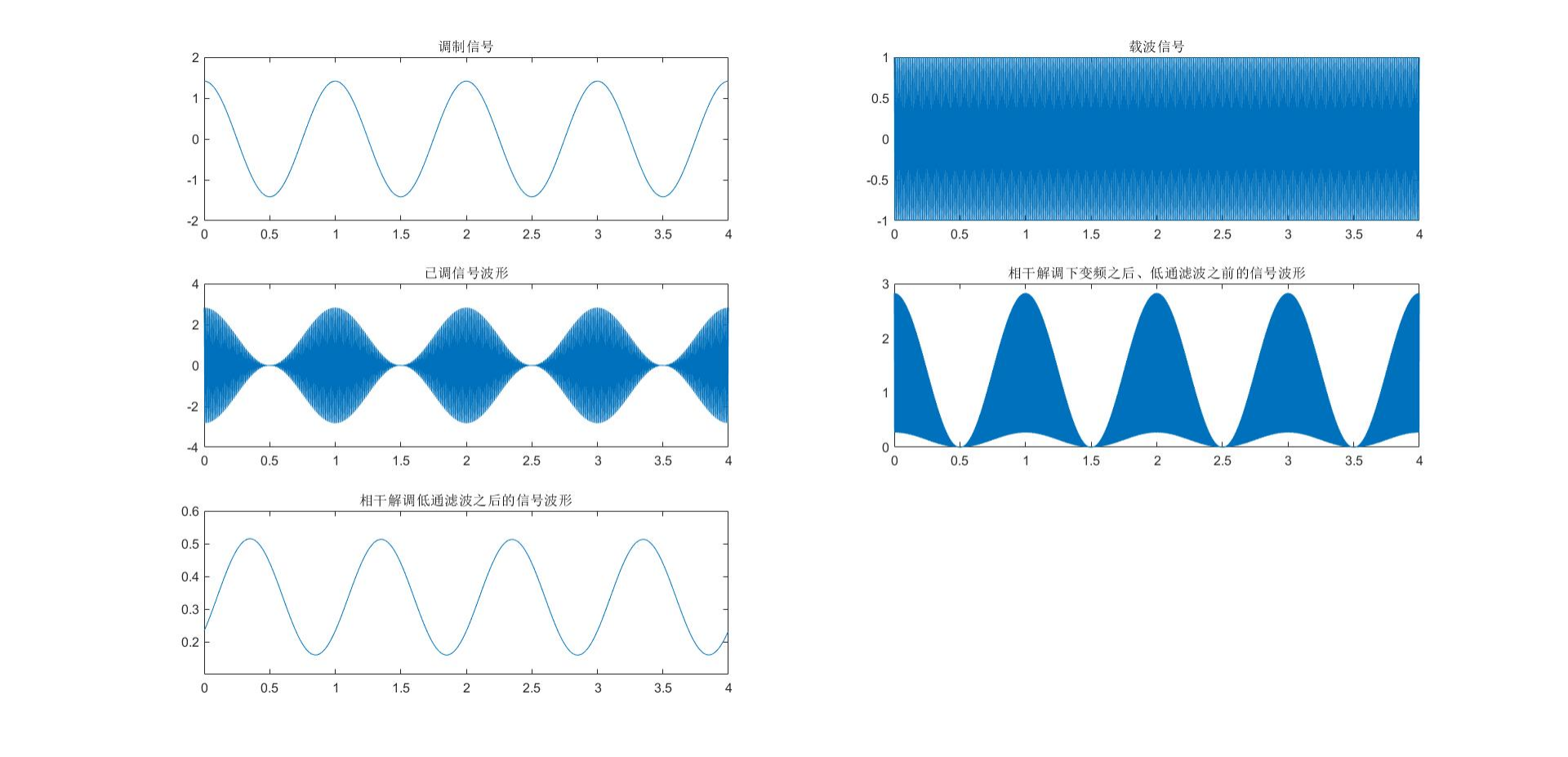
DSB调制

DSB调制相关的图像如上所示。已调信号的包络不能完全反映调制信号的波形。

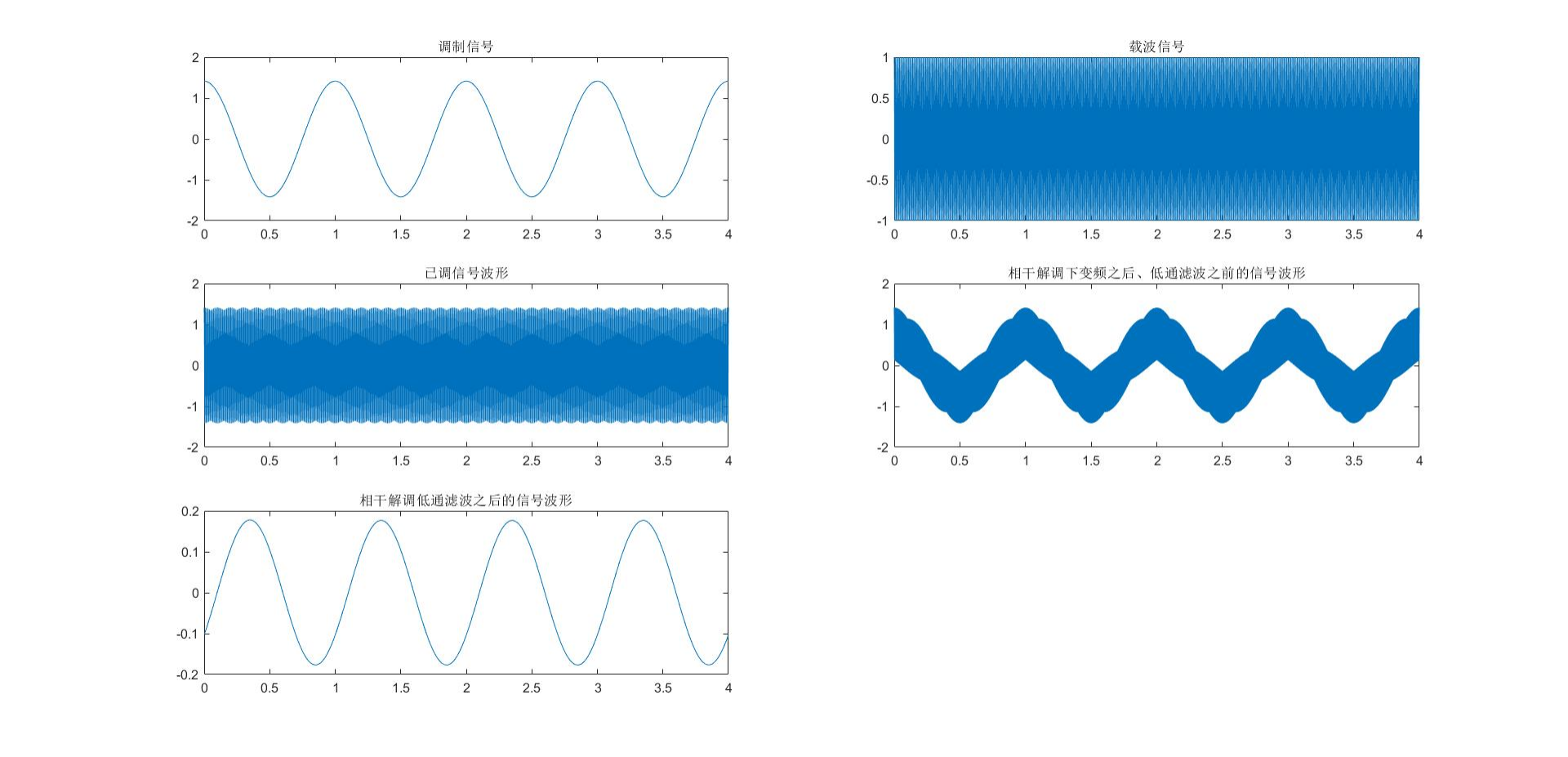
SSB调制

SSB调制相关的图像如上所示。已调信号的包络也不能完全反映调制信号的波形。

实验代码

AM

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
dt=0.001;
fm=1;
fc=100;
T=4;
t=0:dt:T;
mt=sqrt(2)*cos(2*pi*fm*t);%信号源
subplot(3,2,1);
plot(t,mt);hold on;
title('调制信号')
s_dsb=modulate(mt,fc,1/dt,'am')
subplot(3,2,2);
plot(t,cos(2*pi*fc*t));hold on;
title('载波信号')
subplot(3,2,3);
plot(t,s_dsb,t,mt);hold on;
title('已调信号波形及其包络');
rt=s_dsb.*cos(2*pi*fc*t);
subplot(3,2,4);
plot(t,rt);hold on;
title('相干解调下变频之后、低通滤波之前的信号波形');
[f,rf]=T2F(t,rt);
[t,rt]=bpf(f,rf,0,2*fm);
subplot(3,2,5);
plot(t,rt);hold on;
title('相干解调低通滤波之后的信号波形');

function [f,sf] = T2F(t,st)
    dt=t(2)-t(1);
    T=t(end);
    df=1/T;
    N=length(st);
    f=-N/2 * df : df : N/2*df-df;
    sf = fft(st);
    sf=T/N * fftshift(sf);
end

function [t,st] = F2T(f,sf)
    df=f(2)-f(1);
    Fmx=(f(end)-f(1)+df);
    dt=1/Fmx;
    N=length(sf);
    T=dt*N;
    t=0:dt:T-dt;
    sff=ifftshift(sf);
    st=Fmx*ifft(sff);
end

function [t,st] = bpf(f,sf,B1,B2)
    df=f(2)-f(1);
    T=1/df;
    hf=zeros(1,length(f));
    bf=[floor(B1/df):floor(B2/df)];
    bf1=floor(length(f)/2)+bf;
    bf2=floor(length(f)/2)-bf;
    hf(bf1)=1/sqrt(2*(B2-B1));
    hf(bf1)=1/sqrt(2*(B2-B1));
    yf=hf.*sf.*exp(-1i*2*pi*f*0.1*T);
    [t,st]=F2T(f,yf);
end

DSB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
dt=0.001;
fm=1;
fc=100;
T=4;
t=0:dt:T;
mt=sqrt(2)*cos(2*pi*fm*t);%信号源
subplot(3,2,1);
plot(t,mt);hold on;
title('调制信号')
s_dsb=modulate(mt,fc,1/dt,'amdsb-tc')
subplot(3,2,2);
plot(t,cos(2*pi*fc*t));hold on;
title('载波信号')
subplot(3,2,3);
plot(t,s_dsb);hold on;
title('已调信号波形');
rt=s_dsb.*cos(2*pi*fc*t);
subplot(3,2,4);
plot(t,rt);hold on;
title('相干解调下变频之后、低通滤波之前的信号波形');
[f,rf]=T2F(t,rt);
[t,rt]=bpf(f,rf,0,2*fm);
subplot(3,2,5);
plot(t,rt);hold on;
title('相干解调低通滤波之后的信号波形');

function [f,sf] = T2F(t,st)
	dt=t(2)-t(1);
	T=t(end);
	df=1/T;
	N=length(st);
	f=-N/2 * df : df : N/2*df-df;
	sf = fft(st);
	sf=T/N * fftshift(sf);
end

function [t,st] = F2T(f,sf)
	df=f(2)-f(1);
	Fmx=(f(end)-f(1)+df);
	dt=1/Fmx;
	N=length(sf);
	T=dt*N;
	t=0:dt:T-dt;
	sff=ifftshift(sf);
	st=Fmx*ifft(sff);
end

function [t,st] = bpf(f,sf,B1,B2)
	df=f(2)-f(1);
	T=1/df;
	hf=zeros(1,length(f));
	bf=[floor(B1/df):floor(B2/df)];
	bf1=floor(length(f)/2)+bf;
	bf2=floor(length(f)/2)-bf;
	hf(bf1)=1/sqrt(2*(B2-B1));
	hf(bf1)=1/sqrt(2*(B2-B1));
	yf=hf.*sf.*exp(-1i*2*pi*f*0.1*T);
	[t,st]=F2T(f,yf);
end

SSB

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
dt=0.001;
fm=1;
fc=100;
T=4;
t=0:dt:T;
mt=sqrt(2)*cos(2*pi*fm*t);%信号源
subplot(3,2,1);
plot(t,mt);hold on;
title('调制信号')
s_dsb=modulate(mt,fc,1/dt,'amssb')
subplot(3,2,2);
plot(t,cos(2*pi*fc*t));hold on;
title('载波信号')
subplot(3,2,3);
plot(t,s_dsb);hold on;
title('已调信号波形');
rt=s_dsb.*cos(2*pi*fc*t);
subplot(3,2,4);
plot(t,rt);hold on;
title('相干解调下变频之后、低通滤波之前的信号波形');
[f,rf]=T2F(t,rt);
[t,rt]=bpf(f,rf,0,2*fm);
subplot(3,2,5);
plot(t,rt);hold on;
title('相干解调低通滤波之后的信号波形');

function [f,sf] = T2F(t,st)
    dt=t(2)-t(1);
    T=t(end);
    df=1/T;
    N=length(st);
    f=-N/2 * df : df : N/2*df-df;
    sf = fft(st);
    sf=T/N * fftshift(sf);
end

function [t,st] = F2T(f,sf)
    df=f(2)-f(1);
    Fmx=(f(end)-f(1)+df);
    dt=1/Fmx;
    N=length(sf);
    T=dt*N;
    t=0:dt:T-dt;
    sff=ifftshift(sf);
    st=Fmx*ifft(sff);
end

function [t,st] = bpf(f,sf,B1,B2)
    df=f(2)-f(1);
    T=1/df;
    hf=zeros(1,length(f));
    bf=[floor(B1/df):floor(B2/df)];
    bf1=floor(length(f)/2)+bf;
    bf2=floor(length(f)/2)-bf;
    hf(bf1)=1/sqrt(2*(B2-B1));
    hf(bf1)=1/sqrt(2*(B2-B1));
    yf=hf.*sf.*exp(-1i*2*pi*f*0.1*T);
    [t,st]=F2T(f,yf);
end

Matlab作业二：非线性调制

用计算机仿真FM调制，其中，调制信号（基带信号）\(m(t)=\cos 2\pi f_mt\)。调制信号与载波频率、幅度、调制指数等参数自定，要求调制信号频率远小于载波频率。信号时长为4个调制信号周期。

画出以下结果：

  1. 输入信号波形；

  2. 载波波形；

  3. 已调信号波形及其包络；

  4. 试用fft分析已调波形功率谱（附加题，只加分，不减分）。

实验结果

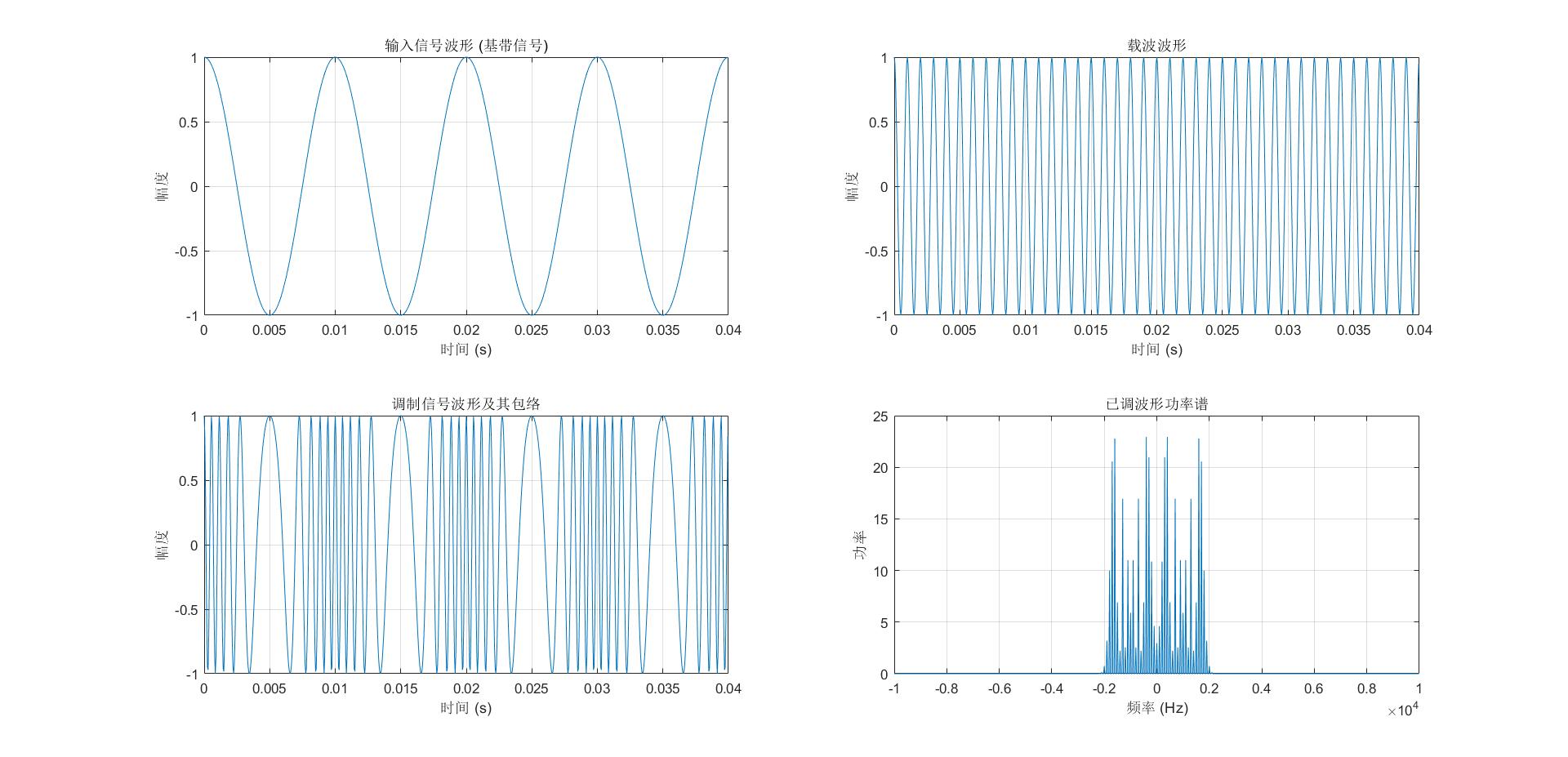
FM调制图像

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
% 参数设置
fm = 100;               % 调制信号频率
fc = 1000;             % 载波频率
kf = 800;               % 调制指数
fs = 20000;            % 采样率
t = 0: 1/fs :4/fm-1/fs;  % 时间向量，4个调制信号周期

% 生成调制信号
m = cos(2*pi*fm*t);    % 基带信号

% 生成载波信号
c = cos(2*pi*fc*t);    % 载波信号

% FM 调制
s = cos(2*pi*fc*t + kf * sin(2 * pi * fm * t) / fm);

% 绘制输入信号波形
subplot(2,2,1);
plot(t, m);
xlabel('时间 (s)');
ylabel('幅度');
title('输入信号波形 (基带信号)');
grid on;

% 绘制载波波形
subplot(2,2,2);
plot(t, c);
xlabel('时间 (s)');
ylabel('幅度');
title('载波波形');
grid on;

% 绘制调制信号波形及其包络
subplot(2,2,3);
plot(t, s);
hold on;
envelope = abs(hilbert(s));    % 计算调制信号包络
% plot(t, envelope, 'r');
hold off;
xlabel('时间 (s)');
ylabel('幅度');
title('调制信号波形及其包络');
% legend('调制信号', '包络');
grid on;

% FFT 分析已调波形的功率谱
subplot(2,2,4);
L = length(s);                  % 信号长度
f = (-fs/2:fs/L:fs/2-fs/L);     % 频率向量
S = fftshift(fft(s));           % 进行 FFT
P = abs(S).^2 / L;              % 计算功率谱
plot(f, P);
xlabel('频率 (Hz)');
ylabel('功率');
title('已调波形功率谱');
grid on;

Matlab作业三：模拟信号数字化

用计算机仿真模拟信号数字化系统过程。量化器为均匀量化，量化范围\([-1,1]\)V；输入信号假设服从均匀分布。二进制信道传输误比特率\(P=10^{-5}\)。

分别仿真得到以下曲线，并将它们绘制在一张图中：

  1. 量化比特\(N=11\)（含符号位）、采用自然码编码时，作出输入信号平均功率从\(-60dBW\)至0dBW（电阻1欧）间变化时输出信噪比变化曲线；
  2. 量化比特\(N=11\)（含符号位）、采用折叠码编码时，作出输入信号平均功率从-60dBW至0dBW（电阻1欧）间变化时输出信噪比变化曲线；
  3. 量化比特\(N=12\)（含符号位）、采用自然码编码时，作出输入信号平均功率从-60dBW至0dBW（电阻1欧）间变化时输出信噪比变化曲线；
  4. 量化比特\(N=12\)（含符号位）、采用折叠码编码时，作出输入信号平均功率从-60dBW至0dBW（电阻1欧）间变化时输出信噪比变化曲线；

关键：如何统计输出信噪比，关键是统计平均输出噪声功率按照输入信号平均功率生成多个（如10000）个样值，对每一个样值作为输入信号，进行量化、编码、信道传输（产生随机误码）和译码，将恢复出的样值与输入样值作差取平方得到样值误差功率。最后，取平均得到平均输出噪声功率。

实验结果

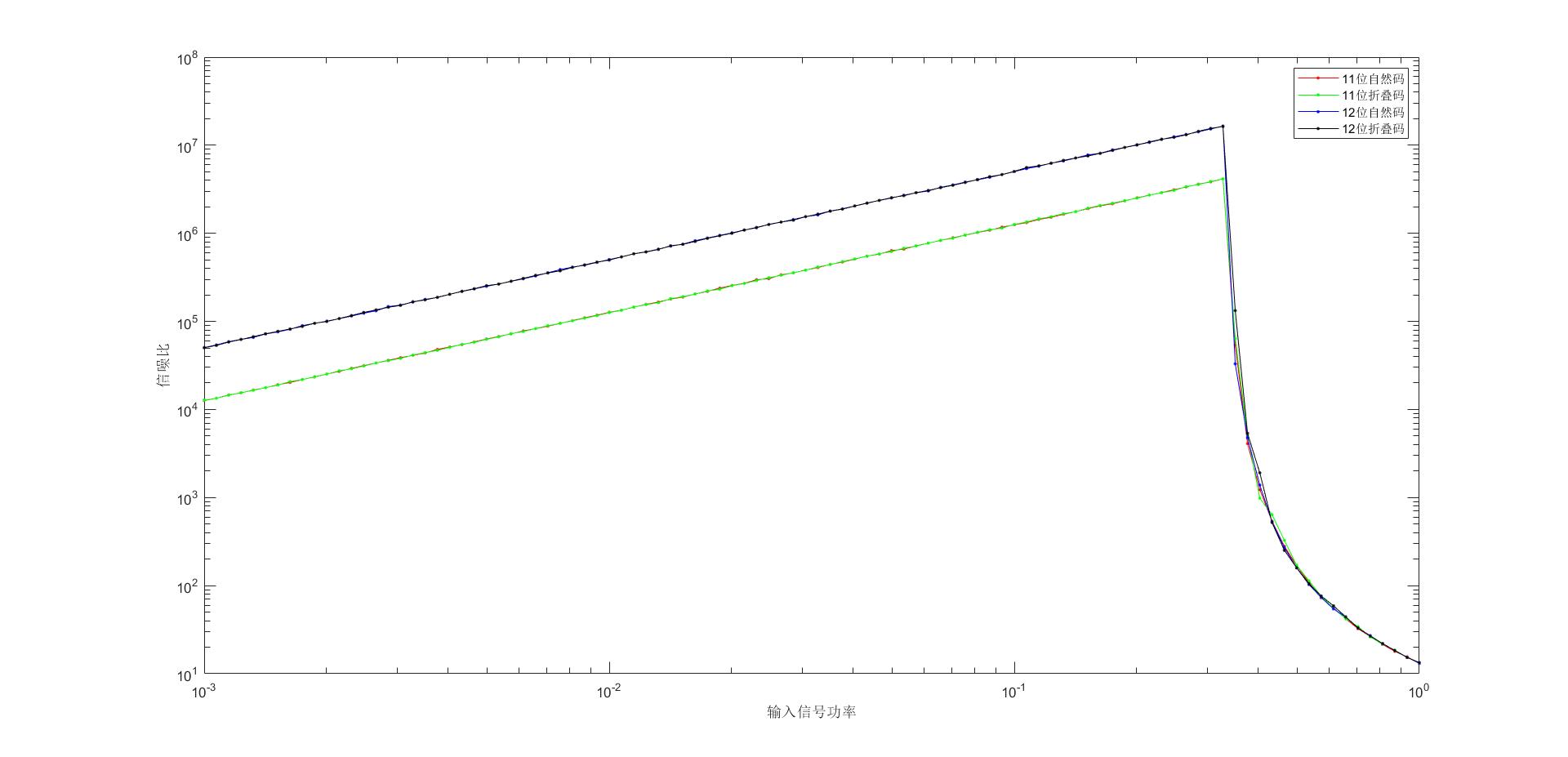
仿真结果图

可以看出：在输入信号功率不大时，信噪比（dB）和功率（dB）成正比。当功率较大时，因为超出了量化范围，所以信噪比急剧减小。

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
% 信号数字化系统仿真模拟

P_in = logspace(-3, 0, 100);  % 平均功率从-60dBW至0dBW（电阻1欧）间变化
SNR1=PCM(P_in,11,0);
SNR2=PCM(P_in,11,1);
SNR3=PCM(P_in,12,0);
SNR4=PCM(P_in,12,1);
loglog(P_in,SNR1,'r.-',P_in,SNR2,'g.-',P_in,SNR3,'b.-',P_in,SNR4,'k.-');
legend('11位自然码', '11位折叠码','12位自然码','12位折叠码');
xlabel('输入信号功率');
ylabel('信噪比');

function SNRs = PCM(P_in,bits,TYPE)
    % 编码，计算信噪比
    % 输入：
    %   P_in：输入信号平均功率测试点
    %   bits：量化比特数（含符号位）
    %   TYPE：码型，0为自然码，1为折叠码
    % 输出：
    %   SNRs：对每个P_in的元素而言的平均噪声功率
    

    qrange = 1;  % 量化范围

    L=length(P_in);
    SNR=zeros(1,100);
    for i = 1:L %对每个功率P_in
    
        % 生成符合功率要求的输入信号
        x_num=10000;
        x = unifrnd(-1,1,1,x_num);
        Px = sum(x .* x) / x_num;
        k = sqrt(P_in(i) / Px);
        x = x.*k;
        
        %量化x
        delta = qrange / (2^(bits-1));
        x_level=floor(abs(x)./delta);
        for j=1:length(x_level)
            if x_level(j)>2^(bits-1)
                x_level(j)=2^(bits-1);
            end
        end
        x_q = sign(x) .* (x_level .* delta + 0.5*delta);
        y_signal=zeros(1,x_num);

        for j = 1:x_num %对x信号中的每个点
            %编码
            x_signal=x_q(j);

            if(x_signal>0)
                x_code='1';
            else
                x_code='0';
            end
            x_bin=dec2bin(x_level(j),bits-1);
            if(TYPE==0) %自然码把对称码按位反转
                x_bin=flip(x_bin);
            end
            x_code=strcat(x_code,x_bin);
            %传输
            BER = 1e-5;  % 误比特率
            y_code=bsc(x_code,BER);
            %译码
            y_bin=extractAfter(y_code,1);
            if(TYPE==0) %自然码把对称码按位反转
                y_bin=flip(y_bin);
            end
            y_level=bin2dec(y_bin);
            y_signal(j)=y_level .* delta + 0.5*delta;
            if(y_code(1)=='0') 
                 y_signal(j) = y_signal(j) * -1;
            end
        end
        error = y_signal - x;
        P_error = sum(error .* error) / x_num;
        SNR(i)=P_in(i) / P_error;
    end
    SNRs=SNR;
end

function y = bsc(x, BER)
    % 二进制对称信道传输
    % 输入：
    %   x：输入比特序列（0或1向量）
    %   BER：误比特率
    % 输出：
    %   y：输出比特序列（0或1向量）
    s=size(x);
    y=zeros(size(x));
    y=char(y);
    for i = 1:s(2)
        flag=rand();
        if(flag>BER)
            y(i)=x(i);
        else
            temp=['1','0'];
            y(i)=temp((x(i)=='0')+1);
        end
    end
end

function y = flip (x)
    %把01字符串序列反转
    %输入：
    %   x：原序列
    %输出：
    %   y：反转序列
    L=length(x);
    y=x;
    for i = 1:L
        if x(i)=='1'
            y(i)='0';
        else
            y(i)='1';
        end
    end
end

Matlab作业四：数字信号基带传输

  1. 用计算机画出升余弦滤波器时域、频域曲线；以及根升余弦滤波器时域、频域曲线。参数自定。

  2. 试用Matlab仿真单极性非归零码、双极性非归零码的误码率，并将其误码率曲线绘制在一张图中。输入信噪比（x轴）变化范围为0:1:15dB，绘图函数semilogy，每个信噪比统计误码率时仿真的点数为1e5。（注：基本方法是随机产生1e5个二进制比特，然后进行码型映射，再给码型叠加噪声（按照信噪比计算噪声功率），最后进行判决，统计误码率）。

实验结果

滤波器
误码率

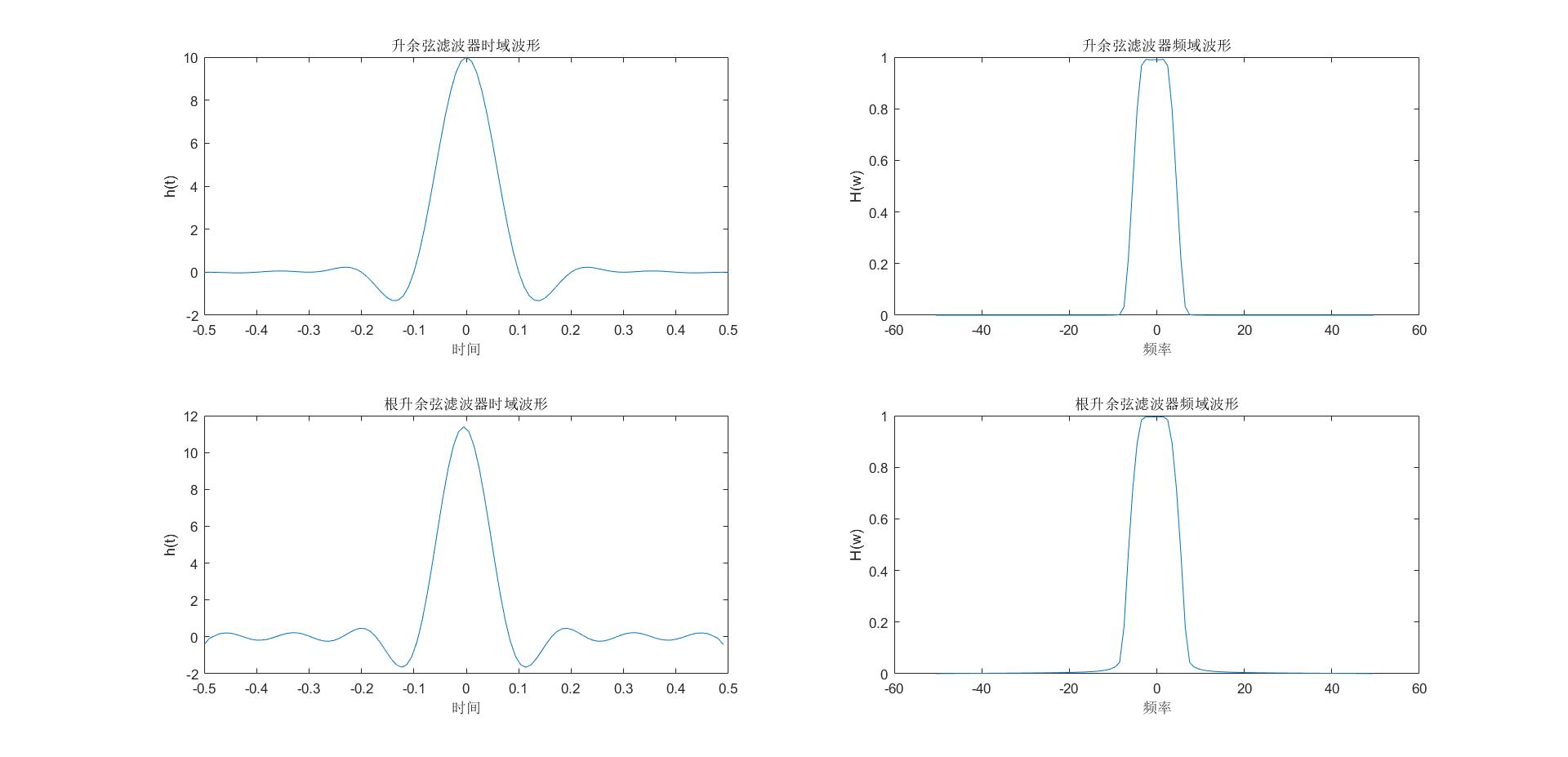
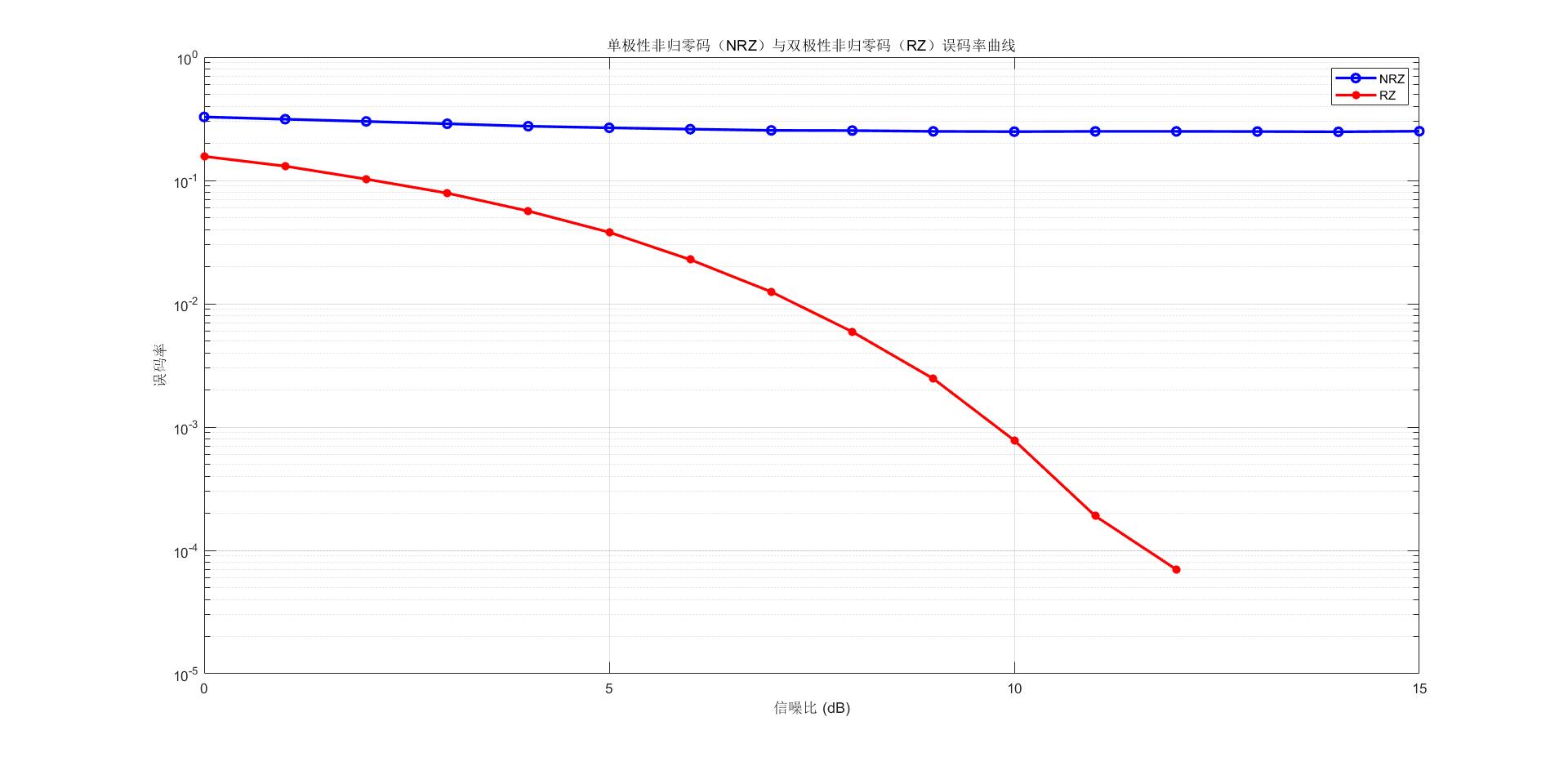
实验代码

滤波器实验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
clear all;
Fs = 100;
Ts = 0.1;
t = -5*Ts:1/Fs:5*Ts;

beta = 0.5; %升余弦滤波器参数

sinc_t=sinc(t/Ts)/Ts; %系数
rc_tnum=cos(pi*beta*t/Ts); %分子
rc_tden=1-(2*beta*t/Ts).^2; %分母
pn=find(abs(rc_tden)<1e-8); %除以零特判
rc_tden(pn) = inf;
rc_t = rc_tnum./rc_tden;
gt = sinc_t .* rc_t;
subplot(2,2,1);
plot(t,gt);
xlabel('时间');
ylabel('h(t)');
title('升余弦滤波器时域波形');

[f,sf]=T2F(t,gt);
subplot(2,2,2);
plot(f,abs(sf));
xlabel('频率');
ylabel('H(w)');
title('升余弦滤波器频域波形');

sf2=sqrt(abs(sf)) .* exp(i*angle(sf));
[t2,st2]=F2T(f,sf2);
subplot(2,2,3);
plot(t2,st2);
xlabel('时间');
ylabel('h(t)');
title('根升余弦滤波器时域波形');


subplot(2,2,4);
plot(f,abs(sf2));
xlabel('频率');
ylabel('H(w)');
title('根升余弦滤波器频域波形');


function [f,sf] = T2F(t,st)
%   时域转频域
%   输入：
%       t：时间
%       st：时间函数
%   输出：
%      f：频率
%      sf：频率函数
    
    dt=t(2)-t(1);
    T=t(end)-t(1);
    df=1.0/T;
    N=length(st);
    f=((-N/2) * df):df:(((N/2)*df)-df);
    sf = fft(st);
    sf=T/N*fftshift(sf);
end

function [t,st] = F2T(f,sf)
    df=f(2)-f(1);
    Fmx=(f(end)-f(1)+df);
    dt=1/Fmx;
    N=length(sf);
    T=dt*N;
    t=-T/2:dt:T/2-dt;
    sff=ifftshift(sf);
    st=Fmx*ifft(sff);
end

误码率实验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
% 仿真参数设置
SNR_dB = 0:1:15;     % 信噪比范围（dB）
numBits = 1e5;       % 仿真比特数

BER_NRZ = zeros(size(SNR_dB));
BER_RZ = zeros(size(SNR_dB));

% 随机产生比特序列
bits = randi([0, 1], 1, numBits);

% 进行误码率仿真
for i = 1:length(SNR_dB)
    % 生成高斯噪声
    noisePower = 10^(-SNR_dB(i)/10);   % 噪声功率
    noise = sqrt(noisePower) * randn(1, numBits);
    
    % 单极性非归零码
    signal_NRZ = bits;     
    receivedSignal_NRZ = signal_NRZ + noise;
    % 判决
    decodedBits_NRZ = receivedSignal_NRZ >= 0;
    % 误码率
    BER_NRZ(i) = sum(bits ~= decodedBits_NRZ) / numBits;
    
    % 双极性非归零码
    signal_RZ = 2*bits - 1;   
    receivedSignal_RZ = signal_RZ + noise;
    % 判决
    decodedBits_RZ = receivedSignal_RZ >= 0;
    % 统计误码率
    BER_RZ(i) = sum(bits ~= decodedBits_RZ) / numBits;
end

% 绘制误码率曲线
semilogy(SNR_dB, BER_NRZ, 'b-o', 'LineWidth', 2);
hold on;
semilogy(SNR_dB, BER_RZ, 'r-*', 'LineWidth', 2);
hold off;

xlabel('信噪比 (dB)');
ylabel('误码率');
title('单极性非归零码（NRZ）与双极性非归零码（RZ）误码率曲线');
legend('NRZ', 'RZ');
grid on;

上机实验二：PCM 编码调制的 Matlab 实现

设模拟信号\(x(t)=0.1\cos(0.15t)+1.5\sin (2.5t)+0.5\cos(4t)\)，选取适当的抽样频率（需要满足无失真采样要求）。

  1. 采用均匀量化，量化层数为各自学号的后四位mod（4）+4（例如学号为 19835412，后四位5412除以4求余为0，再加4为4），请设计均匀量化编码程序。
  2. 采用非均匀量化，设计A律13折线法的PCM编码程序

要求输出：

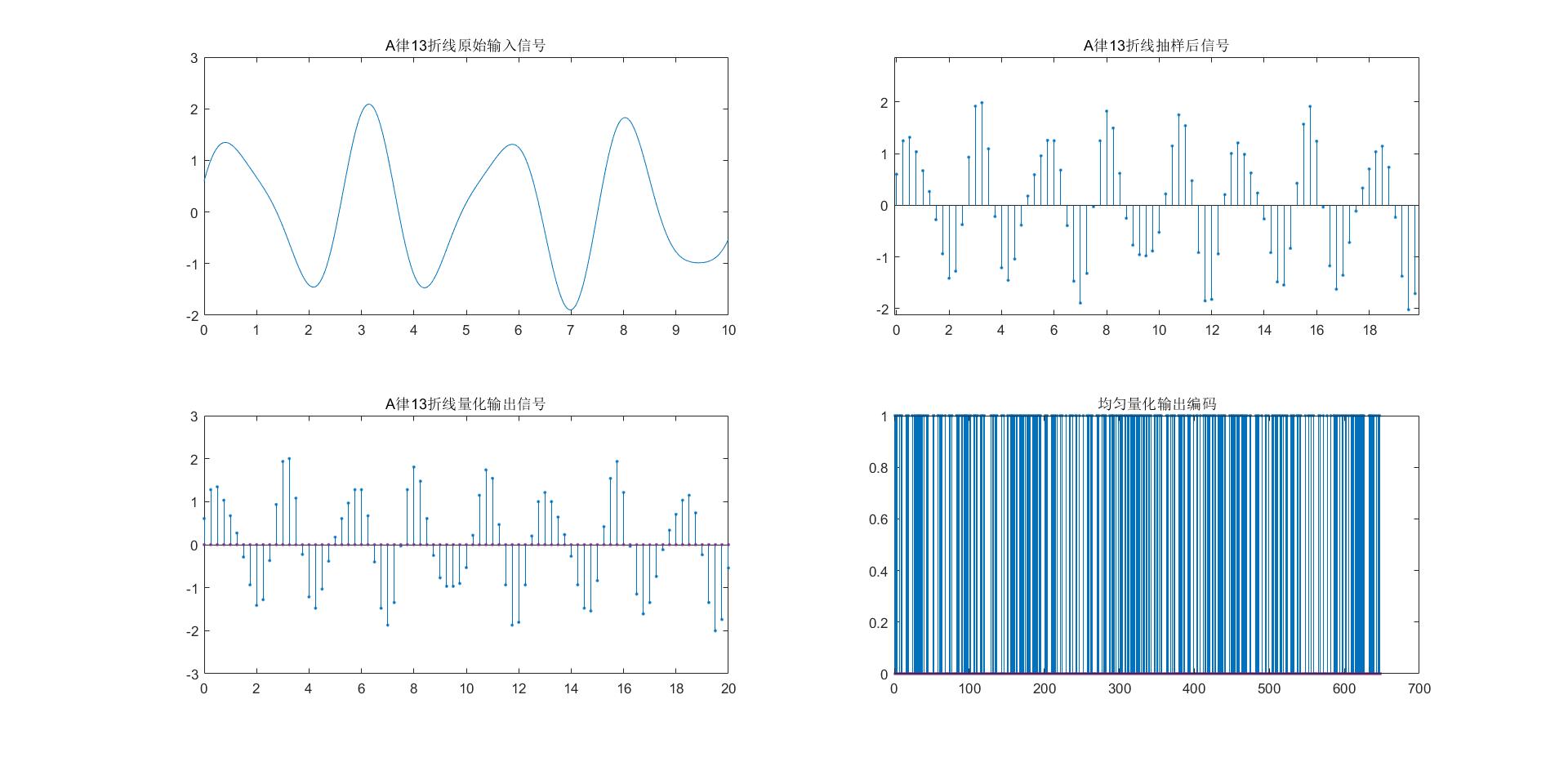
  1. 原始输入信号
  2. 抽样后信号
  3. 量化输出信号
  4. 编码结果

实验结果

均匀量化
A律13折线量化

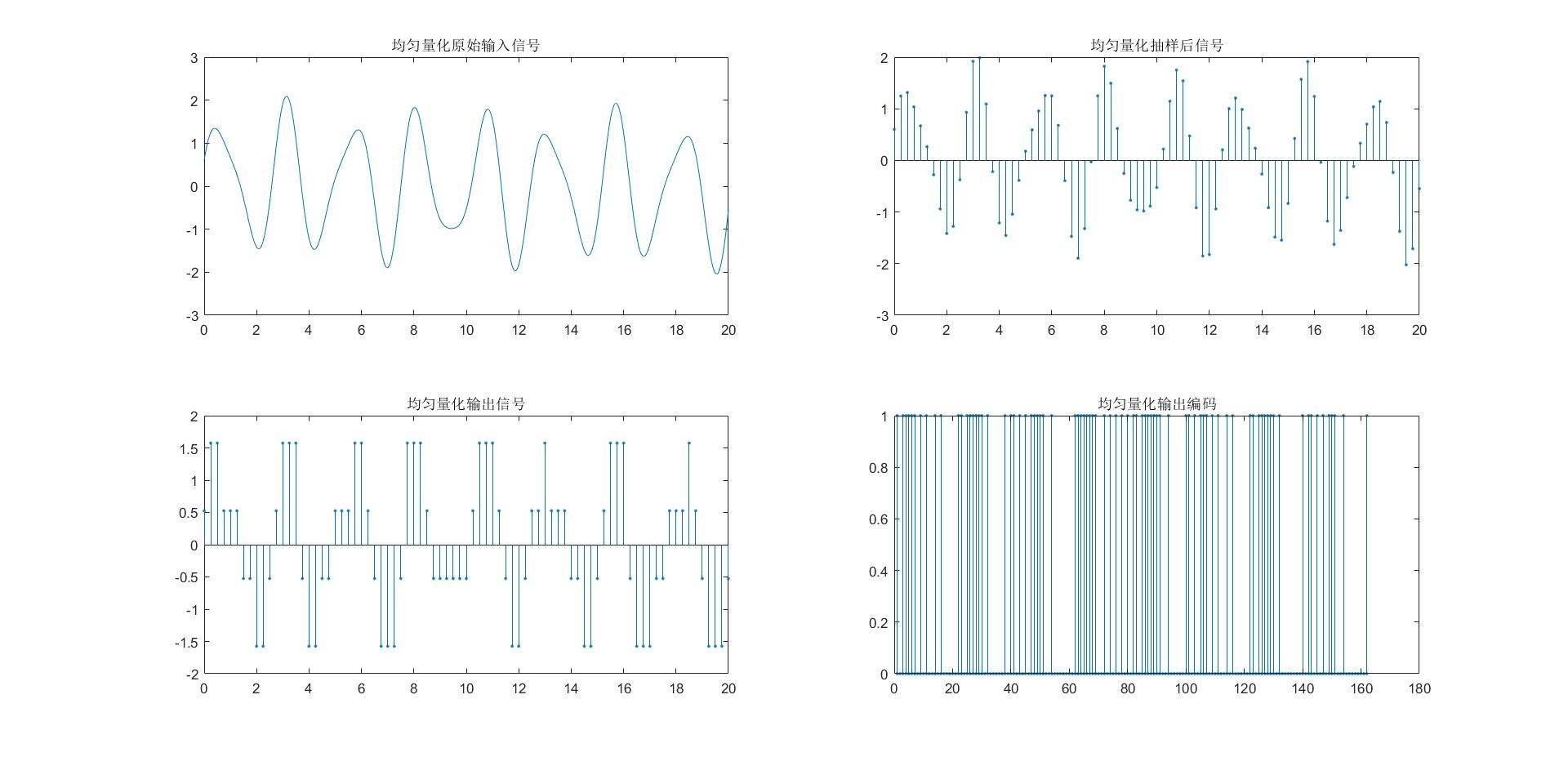
实验代码

均匀量化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
dt=0.01;
t=[0:dt:20];
xt=0.1.*cos(0.15.*t)+1.5.*sin(2.5.*t)+0.5.*cos(4.*t);
subplot(2,2,1);
plot(t,xt);
title("均匀量化原始输入信号");

%抽样
fs=4;
sdt=1/fs;
t1=[0:sdt:20];
xt1=0.1.*cos(0.15.*t1)+1.5.*sin(2.5.*t1)+0.5.*cos(4.*t1);
subplot(2,2,2);
stem(t1,xt1,'.');
title("均匀量化抽样后信号");

%量化
N=mod(5412,4)+4; %量化层数 为学号后四位%4+4
a=2.1; %幅度最大值
reg=[-a,a];
delta=(2*a/N);
x_qt=xt1;
bit=ceil(log2(N));
code='';
L=length(t1);
for i = 1:L
    for j = 0:N
        low=-a+j*delta;
        high=low+delta;
        if (low<=xt1(i) && xt1(i)<=high)
            x_qt(i)=low+delta/2;
            code=strcat(code,dec2bin(j,bit));
        end
    end
end
subplot(2,2,3);
stem(t1,x_qt,'.');
title("均匀量化输出信号");
code

code_in_num=zeros(bit*L);
for i = 1:bit*L
    if(code(i)=='0')
        code_in_num(i)=0;
    end
    if(code(i)=='1')
        code_in_num(i)=1;
    end
end
subplot(2,2,4);
stem(1:bit*L,code_in_num,'.');
title("均匀量化输出编码");

非均匀量化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
dt=0.01;
t=[0:dt:10];
xt=0.1.*cos(0.15.*t)+1.5.*sin(2.5.*t)+0.5.*cos(4.*t);
subplot(2,2,1);
plot(t,xt);
title("A律13折线原始输入信号");

fs=4;
sdt=1/fs;
t1=[0:sdt:20];
xt1=0.1.*cos(0.15.*t1)+1.5.*sin(2.5.*t1)+0.5.*cos(4.*t1);
subplot(2,2,2);
stem(t1,xt1,'.');
title("A律13折线抽样后信号");

code='';
a=2.1;
L=length(xt1);
x_qt=zeros(L);
for i = 1:L
    codei='';
    flag=0;
    x=floor(xt1(i)/a*2048);
    if(x>0)
        codei=strcat(codei,'1');%符号码
        flag=1;
    else
        codei=strcat(codei,'0');
        x=-x;
        flag=-1;
    end
    
    start_level=[0,16,32,64,128,256,512,1024,2048]; %段落码电平范围
    interval   =[1,1, 2, 4, 8,  16, 32, 64]; %量化间隔
    for j = 1:(length(start_level)-1)
        if(start_level(j)<x && x<=start_level(j+1))
            codei=strcat(codei,dec2bin(j,3));%段落码
            temp=floor( ( x-start_level(j) )/interval(j) );
            codei=strcat(codei,dec2bin(temp,4));%段内码
            x_qt(i)=flag*(start_level(j)+interval(j)*(temp+0.5))*(a/2048);
            %恢复量化电平
            break;
        end   
    end
    code=strcat(code,codei);
end

subplot(2,2,3);
stem(t1,x_qt,'.');
title("A律13折线量化输出信号");

bit=8;
code_in_num=zeros(bit*L);
for i = 1:bit*L
    if(code(i)=='0')
        code_in_num(i)=0;
    end
    if(code(i)=='1')
        code_in_num(i)=1;
    end
end
subplot(2,2,4);
stem(1:bit*L,code_in_num,'.');
title("均匀量化输出编码");

仿真实验资料

通信原理虚拟仿真资料下载

提醒一下哈，这个软件很逆天，你直接双击这个文件是打不开的，得先到那个专用的网站里打开实验，然后等软件弹出，再在软件里面通过“打开文件”的方式才能打开这个文件。

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

实验
#Matlab #通信原理
通信原理Matlab软件作业
https://suzumiyaakizuki.github.io/2023/06/30/通信原理Matlab软件作业/
作者
SuzumiyaAkizuki
发布于
2023年6月30日
许可协议