数字图像处理实验报告

数图成绩出来了，实验是满分，所以把报告和代码发出来给大家参考一下。

实验一 图像变换实验

实验目的

学会对图像进行傅立叶等变换，在频谱上对图像进行分析，增进对图像频域上的感性认识，并用图像变换进行压缩。

实验内容

对Lena或cameraman图像进行傅立叶、离散余弦、哈达玛变换。在频域，对比他们的变换后系数矩阵的频谱情况，进一步，通过逆变换观察不同变换下的图像重建质量情况。

实验要求

实验采用获取的图像，为灰度图像，该图像每象素由8比特表示。具体要求如下：

  1. 对图像进行傅立叶变换、获得变换后的系数矩阵；

  2. 将傅立叶变换后系数矩阵的频谱用图像输出，观察频谱；

  3. 通过设定门限，将系数矩阵中95%的（小值）系数置为0，对图像进行反变换，获得逆变换后图像；

  4. 观察逆变换后图像质量，并比较原始图像与逆变后的峰值信噪比（PSNR）。

  5. 对输入图像进行离散余弦、哈达玛变换，重复步骤1-5；

  6. 比较三种变换的频谱情况、以及逆变换后图像的质量（PSNR）。

  7. 比较相同图像质量（PSNR）下，步骤（3）中三种变换的系数矩阵，最少需要保留的非零元素个数。一般而言，需要保留的非零元素越少，则将这种变换用于图像编码，越易于节省码率。

实验原理

图像傅里叶变换（Fourier Transform）是一种常用的信号处理技术，用于将图像从空域（时域）转换到频域。它基于傅里叶分析的原理，将图像表示为一系列频率分量的和，从而揭示了图像中不同频率的信息。

图像傅里叶变换的基本思想是，将一个图像视为不同频率的正弦和余弦波的叠加。通过将图像转换到频域，我们可以得到图像的频谱信息，即不同频率分量的幅度和相位。这使得我们能够分析图像中的高频、低频等特征，并进行一些相关的处理。、

离散余弦变换将一个图像从空域（时域）转换为频域。与傅里叶变换类似，它将图像表示为一系列频率分量的和，但DCT更适合于图像压缩应用，因为它将图像的大部分能量集中在较低频率分量上。

图像哈达玛变换的基本原理是基于哈达玛矩阵的线性变换。哈达玛矩阵是一种特殊的正交变换矩阵，具有正交、可逆和对称的性质。

实验结果与分析

首先将系数矩阵中95%的（小值）系数置为0，对图像进行反变换，获得逆变换后图像：

e1
变换类型 离散傅里叶变换 离散余弦变换 哈达玛变换
峰值信噪比PSNR 30.2933 31.5249 28.5448

然后固定取门限后图像的峰值信噪比为PSNR=28.01，得各种变换需要置0的系数比例为：

变换类型 离散傅里叶变换 离散余弦变换 哈达玛变换
置0的系数比例 0.975 0.9825 0.9575

可以看出，在三种变换中，离散余弦变换DCT是最适合进行图像压缩的一种。由频谱可以看出，傅里叶变换和离散余弦变换的频谱均有较明显的能量集中特性，变换域大值聚集在一小块区域，表现出来就是区域灰度值远高于其他区域，呈现亮色。由于这种特性，在变换域去掉 95%小值不至于对原图像效果产生太大影响

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
figure=imread('lena_std.tif'); 
gray_figure = rgb2gray(figure);%转换为灰度
gray_figure = im2uint8(gray_figure);%转换为8bit
Size=size(gray_figure);
figure(1)
subplot(4,3,1);
imshow(gray_figure);
title('Lena 原图');

tic
fourier = fft2(gray_figure); 
shiftf=fftshift(fourier); %将零频分量移到频谱中心
toc
R=real(shiftf); % 傅立叶变换实部
I=imag(shiftf); % 傅立叶变换虚部
spec = sqrt(R.^2+I.^2); % 幅值
spec_norm =(spec-min(min(spec)))/(max(max(spec))-min(min(spec)))*255; % 归一化
subplot(4,3,2);
imshow(spec_norm); % 显示原图像的频谱
title('傅立叶变换的频谱图');

shiftf=threshold(shiftf,0.975);%0.975
refigure=ifft2(ifftshift(shiftf))/256 ;
subplot(4,3,3);
imshow(refigure);
imwrite(refigure, 'E1_output_image.tif', 'tif');
title('取门限后傅里叶变换还原图像');
PSNR = grayPSNR(gray_figure,256*refigure,8); %计算 PSNR
PSNR

subplot(4,3,4);
imshow(gray_figure);
title('Lena 原图');

tic
DCT=dct2(gray_figure); %离散余弦变换
toc
subplot(4,3,5);
imshow(abs(DCT),[0 255]);
title('离散余弦变换')

DCT=threshold(DCT,0.9825);%0.9825
refigure=idct2(DCT);
subplot(4,3,6);
imshow(refigure,[0 255]);
title('取门限后离散余弦变换还原图像');
PSNR = grayPSNR(gray_figure,refigure,8); %计算 PSNR
PSNR

subplot(4,3,7);
imshow(gray_figure);
title('Lena 原图');

tic
H=hadamard(Size(1));%哈达玛矩阵
gray_figure=double(gray_figure);
DHT=H*gray_figure*H./(512^2);
toc
subplot(4,3,8);
imshow(DHT*2^10,[0,255]);
title('哈达玛变换')

DHT=threshold(DHT,0.9575);%0.9575
refigure=H*DHT*H;
subplot(4,3,9);
imshow(refigure,[0,255]);
title('取门限后哈达玛变换还原图像');
PSNR = grayPSNR(gray_figure,refigure,8); %计算 PSNR
PSNR

% fourier = fft2(gray_figure); 
% shiftf=fftshift(fourier); 
% P=0.9:0.005:1.0;
% PSNRs=zeros(size(P));
% S=size(P);
% for i=1:S(2)
%     shiftf_temp=threshold(shiftf,P(i));
%     refigure=ifft2(ifftshift(shiftf_temp))/256 ;
%     PSNRs(i)=grayPSNR(gray_figure,256*refigure,8);
% end
% subplot(4,3,10);
% plot(P,PSNRs);

function PSNR = grayPSNR(img1,img2,bit)
%   计算图像的峰值信噪比PSNR
%   输入：
%       img1：标准图像
%       img2：待比较图像
%       bit：图像每像素比特数
%   输出：
%       PSNR：峰值信噪比（dB）
    Size=size(img1);
    h=Size(1);
    w=Size(2);
    MAX=2^bit-1;
    img1=double(img1);
    img2=double(img2);
    MSE=sum(sum((img1-img2).^2))/(h*w);     % 均方差  
    PSNR=20*log10(MAX/sqrt(MSE));
end

function matrix = threshold(mat,P)
%   保留矩阵一定比例的数值而把其它点置零
%   输入：
%       mat：待操作矩阵，复数按幅值算
%       P：保留的比例（前P大的数值将被保留）
%   输出：
%       matrix：操作后的矩阵
    matrix=mat;
    Size=size(mat);
    height=Size(1);
    width=Size(2);
    R=real(mat); % 傅立叶变换实部
    I=imag(mat); % 傅立叶变换虚部
    spec = sqrt(R.^2+I.^2); % 幅值
    spec_sort=sort(reshape(spec,[1,width*height]));%排序，取阈值
    limit=spec_sort(round(width*height*P)); %门限
    matrix(spec<limit)=0;
end

问题

在本实验中，助教会要求你就某一个变换为例，作出取门限的保留比例和图像PSNR的折线图，也就是上面代码中注释掉的那一部分。

备注：期末考试中考了哈达玛变换的编程题。

实验二 图像增强复原实验

实验目的

利用空间均值滤波和空间中值滤波对降质图像进行复原，比较不同滤波器处理后的图像间的差异与滤波器大小对结果的影响。

实验内容

  1. 利用空间均值滤波方法进行图像增强复原；

  2. 利用空间中值滤波方法进行图像增强复原。

实验要求

  1. 输入图像采用实验1所获取的图像，编程实现为输入图像添加高斯噪声与椒盐（脉冲）噪声，程序需要能够指定噪声的均值和方差或两个噪声分量中每一个的概率。

  2. 对每一种方法通过计算复原出来的图像的峰值信噪比，比较不同空间掩码的大小的选择对去噪效果的影响。

  3. 将降质图像和利用最优参数恢复后的图像同时显示出来，以便比较。

  4. 实验部分应包括高斯噪声和椒盐噪声的生成过程，原始图像和添加噪声后的图像；加噪图像通过均值和中值滤波器后的结果及比较不同滤波器处理后的图像之间的差异，滤波器大小对结果的影响。

实验原理

空间均值滤波算法的基本思想是，对于图像中的每个像素，将其与周围像素的灰度值进行平均，然后用平均值来替代原始像素的灰度值。这样可以消除图像中的高频噪声，并减少图像中的细节信息。

空间中值滤波算法的基本思想是，在给定的邻域窗口内，将窗口内的像素按照灰度值进行排序，然后选择排序后的中间值作为当前像素的新值。这种方法能够有效地消除图像中的椒盐噪声和其他类型的离群值，同时保留图像的边缘信息。

实验结果与分析

实验2图像结果
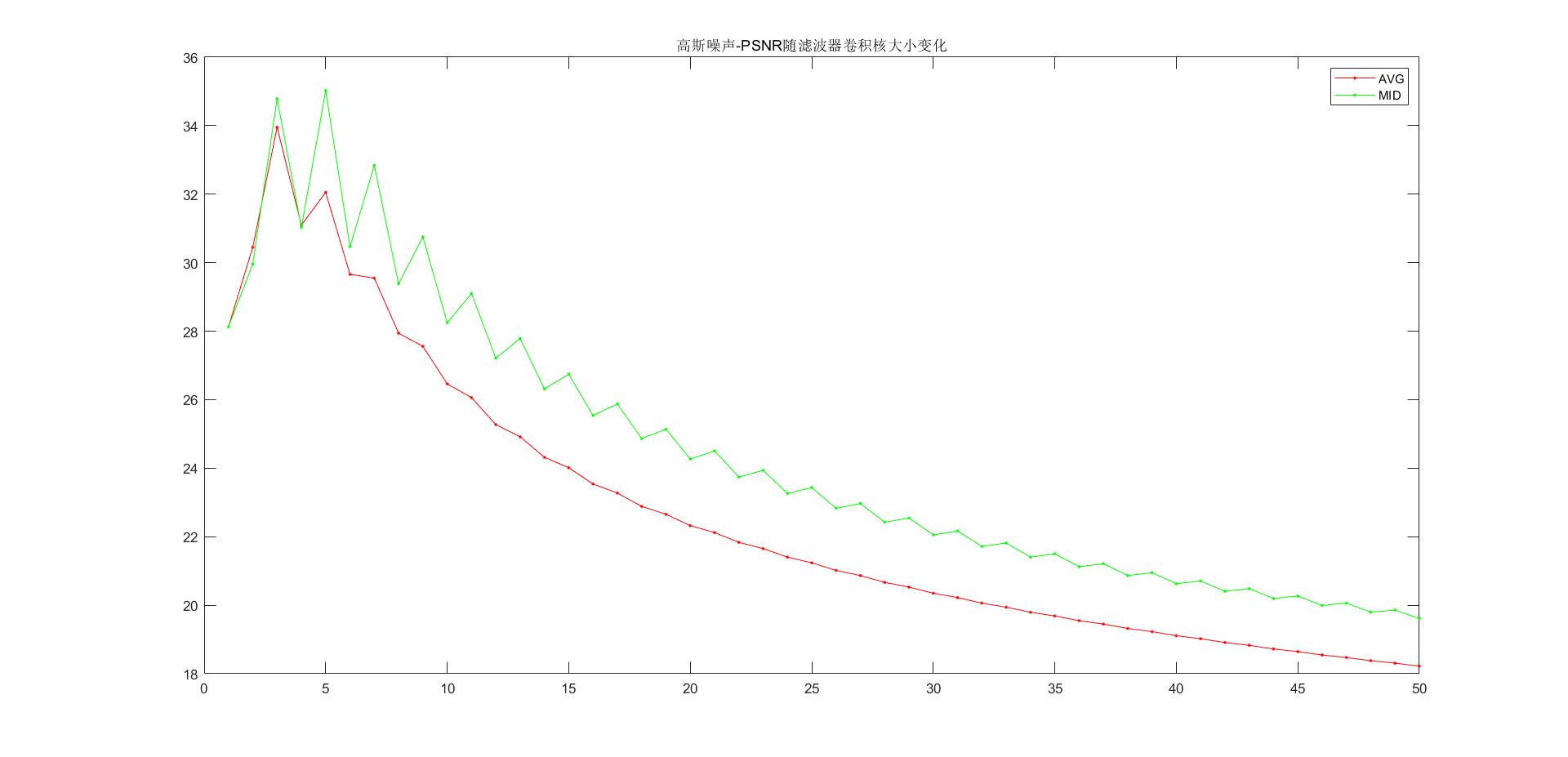加高斯噪声图像PSNR随滤波器卷积核大小变化
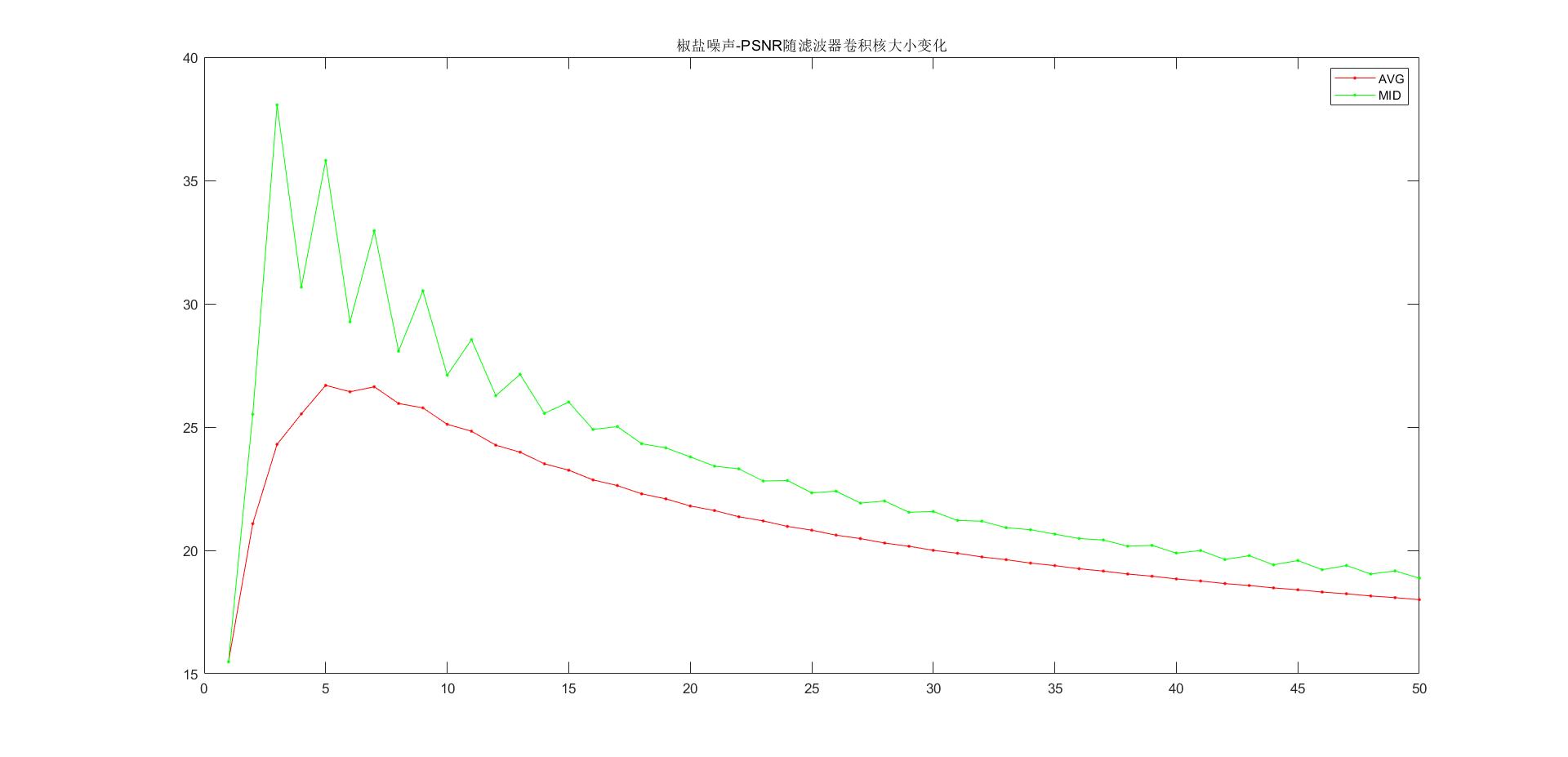加椒盐噪声图像PSNR随滤波器卷积核大小变化

从结果上来看，在椒盐噪声上，中值滤波的效果一般来说好于均值滤波；在高斯噪声上，两者性能差不多。

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
clear all;
img=imread('E1_output_image.tif'); 
figure(1);
subplot(2,5,1);
imshow(img);
title('原图');

mean = 0;  % 均值
variance = 100;  % 方差
noise = mean + sqrt(variance) * randn(size(img));  % 高斯噪声
noisy_img = double(img) + noise;  % 添加噪声
noisy_img = uint8(noisy_img);  % 转回uint8类型
subplot(2,5,2);
imshow(noisy_img);
title('添加高斯噪声后图像');
grayPSNR(img,noisy_img,8)

% 定义滤波器大小
filter_size = 3;
% 对图像进行均值滤波
avg_filtered_img = imfilter(noisy_img, fspecial('average', [filter_size filter_size]));
subplot(2,5,3);
imshow(avg_filtered_img);
title('高斯噪声-均值滤波');

mid_filtered_img = medfilt2(noisy_img, [filter_size filter_size]);
subplot(2,5,4);
imshow(mid_filtered_img);
title('高斯噪声-中值滤波');

MAX_FLITER=50;
avg_PSNR=zeros(1,MAX_FLITER);
mid_PSNR=zeros(1,MAX_FLITER);

for i = 1:MAX_FLITER
    filter_size=i;
    avg_filtered_img = imfilter(noisy_img, fspecial('average', [filter_size filter_size]));
    mid_filtered_img = medfilt2(noisy_img, [filter_size filter_size]);
    avg_PSNR(i)=grayPSNR(img,avg_filtered_img,8);
    mid_PSNR(i)=grayPSNR(img,mid_filtered_img,8);
end

filter_size=5;
mid_filtered_img = medfilt2(noisy_img, [filter_size filter_size]);
subplot(2,5,5);
imshow(mid_filtered_img);
title('高斯噪声-最优参数恢复效果（size=5，中值滤波）');

subplot(2,5,6);
imshow(img);
title('原图');

% 添加椒盐噪声
density = 0.05;  % 椒盐噪声比例
salt_pepper = rand(size(img));  % 随机数矩阵
sp_noisy_img=img;
sp_noisy_img(salt_pepper < density) = 0;  % 添加椒噪声
sp_noisy_img(salt_pepper > 1 - density) = 255;  % 添加盐噪声
subplot(2,5,7);
imshow(sp_noisy_img);
title('添加椒盐噪声后图像');
grayPSNR(img,sp_noisy_img,8)

% 定义滤波器大小
filter_size = 3;
% 对图像进行均值滤波
sp_avg_filtered_img = imfilter(sp_noisy_img, fspecial('average', [filter_size filter_size]));
subplot(2,5,8);
imshow(sp_avg_filtered_img);
title('椒盐噪声-均值滤波');

sp_mid_filtered_img = medfilt2(sp_noisy_img, [filter_size filter_size]);
subplot(2,5,9);
imshow(sp_mid_filtered_img);
title('椒盐噪声-中值滤波');

MAX_FLITER=50;
sp_avg_PSNR=zeros(1,MAX_FLITER);
sp_mid_PSNR=zeros(1,MAX_FLITER);

for i = 1:MAX_FLITER
    filter_size=i;
    sp_avg_filtered_img = imfilter(sp_noisy_img, fspecial('average', [filter_size filter_size]));
    sp_mid_filtered_img = medfilt2(sp_noisy_img, [filter_size filter_size]);
    sp_avg_PSNR(i)=grayPSNR(img,sp_avg_filtered_img,8);
    sp_mid_PSNR(i)=grayPSNR(img,sp_mid_filtered_img,8);
end

filter_size=3;
sp_mid_filtered_img = medfilt2(sp_noisy_img, [filter_size filter_size]);
subplot(2,5,10);
imshow(sp_mid_filtered_img);
title('椒盐噪声-最优参数恢复效果（size=3，中值滤波）');

figure(2)
plot(1:MAX_FLITER,avg_PSNR,'r.-',1:MAX_FLITER,mid_PSNR,'g.-');
title('高斯噪声-PSNR随滤波器卷积核大小变化')
legend('AVG','MID');

figure(3);
plot(1:MAX_FLITER,sp_avg_PSNR,'r.-',1:MAX_FLITER,sp_mid_PSNR,'g.-');
title('椒盐噪声-PSNR随滤波器卷积核大小变化');
legend('AVG','MID');

function PSNR = grayPSNR(img1,img2,bit)
%   计算图像的峰值信噪比PSNR
%   输入：
%       img1：标准图像
%       img2：待比较图像
%       bit：图像每像素比特数
%   输出：
%       PSNR：峰值信噪比（dB）
    Size=size(img1);
    h=Size(1);
    w=Size(2);
    MAX=2^bit-1;
    img1=double(img1);
    img2=double(img2);
    MSE=sum(sum((img1-img2).^2))/(h*w);     % 均方差  
    PSNR=20*log10(MAX/sqrt(MSE));
end

问题

在本实验中，助教会根据空间域滤波的基本原理进行提问，你需要了解卷积核和原图相互作用的过程。然后，助教会问如果卷积核的大小为偶数时，卷积的结果会放在哪里。事实上，如果指定偶数大小的核 h，则核的中心是 floor((size(h) + 1)/2)。例如，四元素滤波器 [0.25 0.75 -0.75 -0.25] 的中心是第二个元素 0.75。此滤波器与五元素滤波器 [0 0.25 0.75 -0.75 -0.25] 的滤波结果相同。

实验三 图像分割处理实验

实验目的

  1. 了解图像分割的基本原理，并利用图像分割算法进行图像分割处理；

  2. 掌握数学形态学的基本运算。

实验内容

  1. 利用类间方差阈值算法实现图像的分割处理；

  2. 利用形态学处理进行处理结果修正。

实验要求

  1. 实验用图如图6.2所示；
实验3原始图像

  1. 对输入图像进行平滑处理，以减小噪声对分割处理的影响，比较中值滤波范围取不同值时对图像滤波的效果；

  2. 利用类间方差阈值算法对滤波处理后图像进行分割处理，获取分割图像；

  3. 利用数学形态学中的腐蚀和膨胀运算处理，剔除分割处理结果中的一些细小的残余误分割点，在进行腐蚀和膨胀运算时可采用半径为r的圆形结构元素，注意比较选取不同r值时的处理结果（r分别取1、3、5）。

实验原理

大津法的基本思想是遍历所有可能的阈值，并计算每个阈值下的类间方差。类间方差是衡量图像分割质量的指标，它衡量了不同类别之间的差异程度。通过最大化类间方差，可以找到最佳阈值，以便将图像分成背景和目标两个类别。它的优点在于它是一种自适应的阈值选择方法，不需要预先指定阈值，而是根据图像的特性自动选择最佳阈值。它在处理具有双峰直方图的图像（例如目标和背景明显不同的图像）时表现良好，并且适用于各种类型的图像分割任务。

腐蚀操作通过对图像进行局部最小化来缩小或腐蚀图像中物体的边界，这种操作使图像中的物体边界变得更加平滑，并且可以用于去除小的噪声、分离物体之间的连接以及减小物体的尺寸。膨胀操作通过对图像进行局部最大化来扩展或膨胀图像中物体的边界，这种操作可用于连接物体、填充物体内的空洞、增大物体的尺寸以及消除图像中的小孔洞。

开闭运算是腐蚀和膨胀操作的组合。开运算先进行腐蚀操作，然后再进行膨胀操作。它可以用于平滑图像的轮廓、去除小的物体以及分离连接的物体。闭运算先进行膨胀操作，然后再进行腐蚀操作。它可以用于填充物体内的小孔洞、连接物体以及平滑图像的背景。

实验结果与分析

实验3各图像结果

由实验结果可以看出，中值滤波效果抑制了图像中大部分噪声，而图像也被一定程度地模糊；经过图像分割之后，目标的轮廓被提取出来。开操作方向向外的角变圆滑了，但是方向向内的角未受影响。闭运算方向向内的角变圆滑了，方向向外的角未受影响。

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
img = imread("shiyan3.bmp");
img = rgb2gray(img);
img = im2uint8(img);

figure;
subplot(3, 3, 1);
imshow(img);
title('原始图像');

medianFilteredImages = cell(1,3);
filterSizes = [3, 5, 7];  % 不同的滤波范围
for i = 1:numel(filterSizes)
    medianFilteredImages{i} = medfilt2(img, [filterSizes(i), filterSizes(i)]);
    subplot(3, 3, i+1);
    imshow(medianFilteredImages{i});
    title(['中值滤波 (', num2str(filterSizes(i)), 'x', num2str(filterSizes(i)), ')']);
end

%选择PSNR最大的3x3进行后续操作
medianFilteredImage = medfilt2(img,[3,3]);
segmentedImage = imbinarize(medianFilteredImage);
subplot(3,3,5);
imshow(segmentedImage);
title('分割后图像');

%形态学处理
cleanedSegmentedImages = cell(1,3);
radius = [1,3,5];
for i = 1:numel(radius)
    se = strel('disk',radius(i));
    erodedImage = imerode(segmentedImage, se);%腐蚀
    cleanedSegmentedImages{i} = imdilate(erodedImage,se);%膨胀
    subplot(3,3,5+i);
    imshow(cleanedSegmentedImages{i});
    title(['开运算，半径为',num2str(radius(i))]);
end

se = strel('disk',3);
dilatedImage = imdilate(segmentedImage,se);
cleanedImage = imerode(dilatedImage,se);
subplot(3,3,9);
imshow(cleanedImage);
title('闭运算，半径为3');

function PSNR = grayPSNR(img1,img2,bit)
%   计算图像的峰值信噪比PSNR
%   输入：
%       img1：标准图像
%       img2：待比较图像
%       bit：图像每像素比特数
%   输出：
%       PSNR：峰值信噪比（dB）
    Size=size(img1);
    h=Size(1);
    w=Size(2);
    MAX=2^bit-1;
    img1=double(img1);
    img2=double(img2);
    MSE=sum(sum((img1-img2).^2))/(h*w);     % 均方差  
    PSNR=20*log10(MAX/sqrt(MSE));
end

问题

在本实验中，助教会问大津法的基本原理，类间方差和类内方差的概念，腐蚀与膨胀和开闭运算的基本知识，以及开闭运算的功能。

实验四 用Hough变换进行曲线的参数提取

实验目的

  1. 了解边缘检测算子的原理，并利用边缘算子对图像进行检测；

  2. 掌握Hough变换的基本原理。

实验内容

  1. 分别将原始图像及加高斯噪声、椒盐噪声后的图像中圆形边缘检测出来；

  2. 用Hough变换对边缘进行参数提取。

实验要求

  1. 实验用图像文件：原始图像（houghorg.bmp）、加高斯噪声后图像（houghgau.bmp）和加椒盐噪声后图像（houghsalt.bmp）；
原始图像

  1. 在含有噪声的背景下，先对图像中值滤波，再进行边缘检测；

  2. 将目标的边界提取出来。边缘检测算子可利用自带函数实现，使用Robert、Sobel和Laplacian算子；

  3. 利用Hough变换提取的参数绘制曲线，并叠加在噪声图像上。

实验原理

Robert、Sobel和Laplacian是常用的边缘检测算子，分别运用梯度或二阶微分等原理来对图像的边缘进行检测。

在\((x,y)\)空间中，圆的方程为：

\[ (x - a)^{2} + (y - b)^{2} = r^{2} \]

取\((a,b)\)做变换空间，也因此在\((x,y)\)空间中圆上任意一点\(\left( x_{i},y_{i} \right)\)与\((a,b)\)空间中的圆相对应：

\[ \left( a - x_{i} \right)^{2} + \left( b - y_{i} \right)^{2} = r^{2} \]

在\((x,y)\)空间中所有共圆的点在\((a,b)\)空间中对应的曲线交于\(\left( a_{0},b_{0} \right)\)，利用Hough变换的步骤，最终可以在累加数组中找到\(\left( a_{0},b_{0} \right)\)点出现峰值，从而检测出在\((x,y)\)空间中有一个以\(\left( a_{0},b_{0} \right)\)为半径的圆

实验结果与分析

加高斯噪声实验结果
加椒盐噪声实验结果

观察实验结果，三种算子都能有效提取边界。

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
clear;close all;

imgOrg = imread('houghorg.bmp');
imgOrg = rgb2gray(imgOrg);
imgOrg = mat2gray(imgOrg);

figure(1);
make(imgOrg);

imgSalt = imread('houghsalt.bmp');
imgSalt = mat2gray(imgSalt);
figure(2);
make(imgSalt);

imgGau = imread('houghgau.bmp');
imgGau = mat2gray(imgGau);
figure(3);
make(imgGau);

function edge = edgeRobert(image)
%	Robert算子边缘提取
%   输入：
%       image：待处理图像
%   输出：
%       edge：提取的边缘
    Gx = [ 1  0; 
           0 -1];
    Gy = [ 0  1; 
          -1  0];   

    edgeX = conv2(double(image), Gx, 'same');
    edgeY = conv2(double(image), Gy, 'same');

    edgeMagnitude = sqrt(edgeX.^2 + edgeY.^2);
    edgeMagnitude = mat2gray(edgeMagnitude);
    edge = imbinarize(edgeMagnitude);

end

function edge = edgeStobel(image)
%	Stobelt算子边缘提取
%   输入：
%       image：待处理图像
%   输出：
%       edge：提取的边缘
    Gx = [-1  0  1; 
          -2  0  2; 
          -1  0  1];
    Gy = [ 1  2  1; 
           0  0  0; 
          -1 -2 -1];

    edgeX = conv2(double(image), Gx, 'same');
    edgeY = conv2(double(image), Gy, 'same');

    edgeMagnitude = sqrt(edgeX.^2 + edgeY.^2);
    edgeMagnitude = mat2gray(edgeMagnitude);
    edge = imbinarize(edgeMagnitude);

end

function edge = edgeLaplacian(image)
%	Laplacian算子边缘提取
%   输入：
%       image：待处理图像
%   输出：
%       edge：提取的边缘
    H = fspecial('laplacian');
    edgeResponse = conv2(double(image), H, 'same');
    edgeMagnitude = abs(edgeResponse);
    edgeMagnitude = mat2gray(edgeMagnitude);
    edge = imbinarize(edgeMagnitude);
end

function make(img)
    imgO=img;
    img = medfilt2(img, [9 9]);
    edgeR=edgeRobert(img);
    edgeS=edgeStobel(img);
    edgeL=edgeLaplacian(img);
    subplot(2,3,1);
    imshow(edgeR);
    title('Robert算子边缘提取');
    subplot(2,3,2);
    imshow(edgeS);
    title('Stobel算子边缘提取');
    subplot(2,3,3);
    imshow(edgeL);
    title('Laplacian算子边缘提取');
	
	%以下是Hough变换
    radiusRange = [20 500]; % 圆的半径范围

    [centersR, radiiR, metricR] = imfindcircles(edgeR, radiusRange,'Sensitivity',0.9);
    %Sensitivity是敏感度因子，随着敏感度因子的增大，imfindcircles 会检测到更多圆形目标，包括弱圆形和部分模糊圆形。更高的敏感度值也会增加错误检测的风险。
    [centersS, radiiS, metricS] = imfindcircles(edgeS, radiusRange,'Sensitivity',0.9);
    [centersL, radiiL, metricL] = imfindcircles(edgeL, radiusRange,'Sensitivity',0.9);
    subplot(2,3,4);
    imshow(imgO);
    viscircles(centersR, radiiR,'EdgeColor','b');
    subplot(2,3,5);
    imshow(imgO);
    viscircles(centersS, radiiS,'EdgeColor','b');
    subplot(2,3,6);
    imshow(imgO);
    viscircles(centersL, radiiL,'EdgeColor','b');
end

问题

在本实验中，助教会问你关于Hough变换提取圆形的基本原理。

实验五 手写数字识别

实验目的

掌握分类、识别问题的实质，了解各种分类问题的机器学习方法，并至少掌握一种

实验内容

对实验提供含噪声的手写数据库（MNIST）进行训练和测试，最终能够较为准确的识别数据库中的手写体数字。

实验要求

编写一完整的程序，选取一种合适的机器学习方法，对实验提供的手写数据库（MNIST）进行训练和测试，最终能够较为准确的识别数据库中的手写体数字。

数据文件共分为训练集和测试集：

训练数据集：

Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)

Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)

测试数据集：

Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)

Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)

实验原理

卷积神经网络（Convolutional Neural Network，CNN）是一种深度学习模型，主要用于图像识别、目标检测和图像分类等任务。CNN的组成和原理如下：

卷积层：是CNN的核心组件。它通过使用一系列可学习的卷积核对输入图像进行卷积操作。

激活函：在卷积层的输出特征图上应用非线性激活函数，如ReLU，用于引入非线性变换。ReLU函数将负值置为零，并保留正值。这种非线性变换能够增强网络的表达能力，使其能够学习更复杂的特征。

池化层：用于降低特征图的空间尺寸，减少参数数量，并提取出重要的特征。常用的池化操作是最大池化，它从输入的局部区域中选择最大值作为输出。池化层还可以提供一定程度的平移不变性，使网络对输入的微小变化更加稳定。

全连接层：是在卷积层和输出层之间的一层。它将之前的卷积层或池化层的输出特征图展平为一维向量，并与权重相乘并进行偏置，最后通过激活函数得到最终的分类结果。全连接层能够学习到输入特征之间的复杂关系，用于分类和预测。

输出层：是CNN的最后一层，通常使用softmax函数将网络的输出转换为概率分布，用于多分类问题的预测。

CNN通过多个卷积层、激活函数、池化层和全连接层的堆叠，可以提取图像中的高级特征，并通过反向传播算法进行端到端的训练。通过大规模的数据集训练，CNN能够学习到复杂的特征表示，并在新的未见过的图像上进行准确的分类和预测。

实验结果与分析

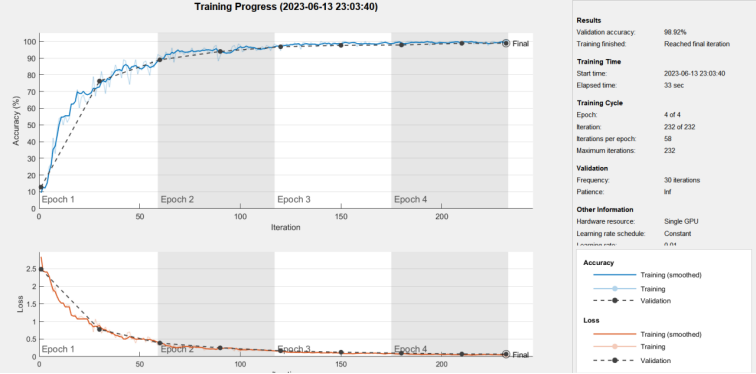训练过程示意图
加噪声前识别示例
加噪声后识别示例
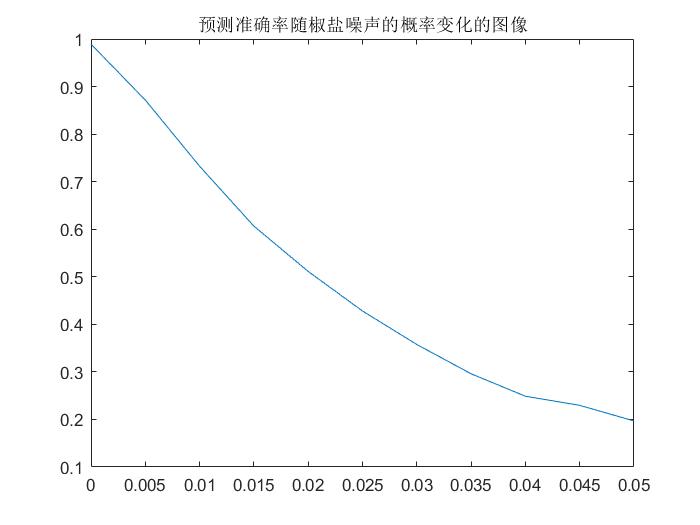预测准确率随噪声变化

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
clear;close all;

digitDatasetPath = fullfile(matlabroot,'toolbox','nnet','nndemos', ...
    'nndatasets','DigitDataset');
imds = imageDatastore(digitDatasetPath, ...
    'IncludeSubfolders',true,'LabelSource','foldernames');
% figure;
% perm = randperm(10000,20);
% for i = 1:20
%     subplot(4,5,i);
%     imshow(imds.Files{perm(i)});
% end

labelCount = countEachLabel(imds)
img = readimage(imds,1);
imageSize = size(img);

numTrainFiles = 750;
[imdsTrain,imdsValidation] = splitEachLabel(imds,numTrainFiles,'randomize');

layers = [
    imageInputLayer([28 28 1]) %图像输入层
    
    convolution2dLayer(3,8,'Padding','same') %卷积层
    batchNormalizationLayer %批量归一化层
    reluLayer %ReLU层
    
    maxPooling2dLayer(2,'Stride',2) %最大池化层
    
    convolution2dLayer(3,16,'Padding','same') 
    batchNormalizationLayer
    reluLayer
    
    maxPooling2dLayer(2,'Stride',2)
    
    convolution2dLayer(3,32,'Padding','same')
    batchNormalizationLayer
    reluLayer
    
    fullyConnectedLayer(10) %全连接
    softmaxLayer
    classificationLayer]; %分类

options = trainingOptions('sgdm', ... %随机梯度下降法
    'InitialLearnRate',0.01, ... %学习率
    'MaxEpochs',4, ... %训练轮数
    'Shuffle','every-epoch', ... %随机化
    'ValidationData',imdsValidation, ... %验证集
    'ValidationFrequency',30, ... %每隔30个训练迭代时进行一次验证
    'Verbose',false, ...
    'Plots','training-progress'); %显示训练过程的进度图

net = trainNetwork(imdsTrain,layers,options);
YPred = classify(net,imdsValidation);
YValidation = imdsValidation.Labels;

%显示20个无噪声识别示意图
figure(1);
perm = randperm(2500,20);
for i = 1:20
    subplot(4,5,i);
    imshow(imdsValidation.Files{perm(i)});
    title('预测值'+string(YPred(perm(i))));
end

%无噪声准确率
accuracy = sum(YPred == YValidation)/numel(YValidation)

newImgArray = ones([imageSize,2500]);
newImgArray2 = ones([imageSize,2500]);


%复制测试集
for i = 1:2500
    newImgArray(:,:,i) = imread(imdsValidation.Files{i});
end
Densitys = 0:0.005:0.05; %椒盐噪声概率
accuracys = ones(size(Densitys));
%加噪声
for i = 1:length(Densitys)
    i
    for j = 1:2500
        p=Densitys(i);
        newImgArray2(:,:,j) = addSaltAndPepperNoise(newImgArray(:,:,j),p);
        YPred(j,:)=classify(net,newImgArray2(:,:,j));
    end
    accuracys(i) = sum(YPred == YValidation)/numel(YValidation);
end
figure(2);
plot(Densitys,accuracys);
title('预测准确率随椒盐噪声的概率变化的图像');

for j = 1:2500
    p=0.01;
    newImgArray2(:,:,j) = addSaltAndPepperNoise(newImgArray(:,:,j),p);
    YPred(j,:)=classify(net,newImgArray2(:,:,j));
end
figure(3);
perm = randperm(2500,20);
for i = 1:20
    subplot(4,5,i);
    imshow(newImgArray2(:,:,perm(i)));
    title('预测值'+string(YPred(perm(i)))+',实际值'+string(YValidation(perm(i))));
end

function noisyImage = addSaltAndPepperNoise(image, noiseDensity)
    % image: 输入的图像
    % noiseDensity: 椒盐噪声概率
    
    salt_pepper = rand(size(image)); 
    noisyImage=image;
    noisyImage(salt_pepper < noiseDensity) = 0;  % 添加椒噪声
    noisyImage(salt_pepper > 1 - noiseDensity) = 255;  % 添加盐噪声
end

问题

在本实验中，助教会问关于CNN基本原理的问题

感悟与总结

在进行图像处理实验的过程中，我通过实践掌握了图像变换、图像增强复原、图像分割、曲线参数提取以及手写数字识别等五个部分的基本技术和方法。这次实验给我带来了许多收获和感悟。

在图像变换方面，我学会了使用离散傅立叶变换、离散余弦变换等方法对图像进行频域分析和压缩。通过观察变换后的系数矩阵的频谱情况，我更深入地理解了图像在频域上的特征表达。

在图像增强复原方面，我学习了空间均值滤波、中值滤波等技术，可以有效地去除图像噪声和模糊，并提升图像的质量和清晰度。这对于图像处理和分析来说非常重要，尤其在实际应用中能够提升图像的可视化效果。

在图像分割方面，我掌握了基于阈值分割和基于边缘检测的方法。通过调整阈值和应用边缘检测算子，我成功地将感兴趣的目标进行提取和分析。

通过学习和实践边缘检测算法和Hough变换，我了解到它在曲线参数提取方面的强大能力。通过投票累加器和阈值设定，我成功地从图像中提取出了曲线的参数。

手写数字识别让我简单认识了深度学习模型（如CNN）在图像分类和识别任务中的卓越性能。通过搭建并训练CNN模型，我能够准确地对手写数字进行分类和识别。

图像处理实验和课内知识结合紧密，通过完成上述五个实验，我对于课内各知识的掌握在实践中得以提升，同时也加强了对Matlab语言的理解和运用能力，提升了自己的综合能力。

实验
#数字图像处理
数字图像处理实验报告
https://suzumiyaakizuki.github.io/2023/06/30/数字图像处理实验报告/
作者
SuzumiyaAkizuki
发布于
2023年6月30日
许可协议