通信原理笔记·数字通信
虽然这里名叫数字通信,但是需要注意的是,数字通信实际包含三部分内容,即
- 数字信号基带传输
- 数字调制
- 差错控制编码
但是因为如果单个文件太大、公式太多,写起来会有点卡顿,看起来也比较费劲,所以拆成两篇文章。这篇文章的主要内容是数字调制和差错控制编码。
数字调制
二进制调制OOK
把幅度为\(2A\)的单极性非归零码按DSB方式进行调制,得到的就是单极性二进制幅移键控(2ASK),也叫二进制启闭键控(OOK),系统框图如下(其实就是DSB调制的框图):
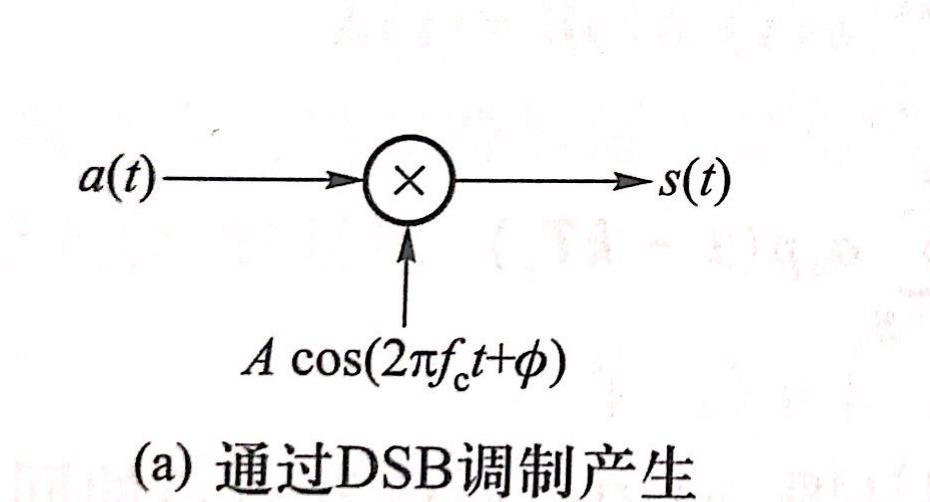
即: \[ s(t)=a(t)\sqrt 2 \cos(2\pi f_ct+\phi) \] 调制信号波形示意图如下:
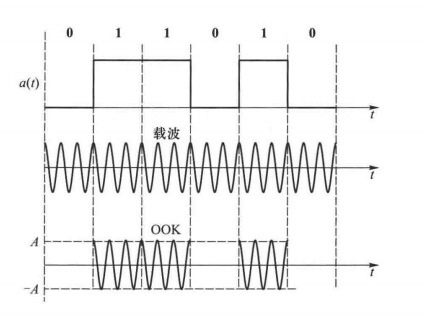
波形功率谱密度为:

可以看出,这个功率谱旁瓣比较高,不是很好。那咋办呢?一种常见的设计就是加个成形滤波。我们采用根升余弦成形滤波,则波形图如下:
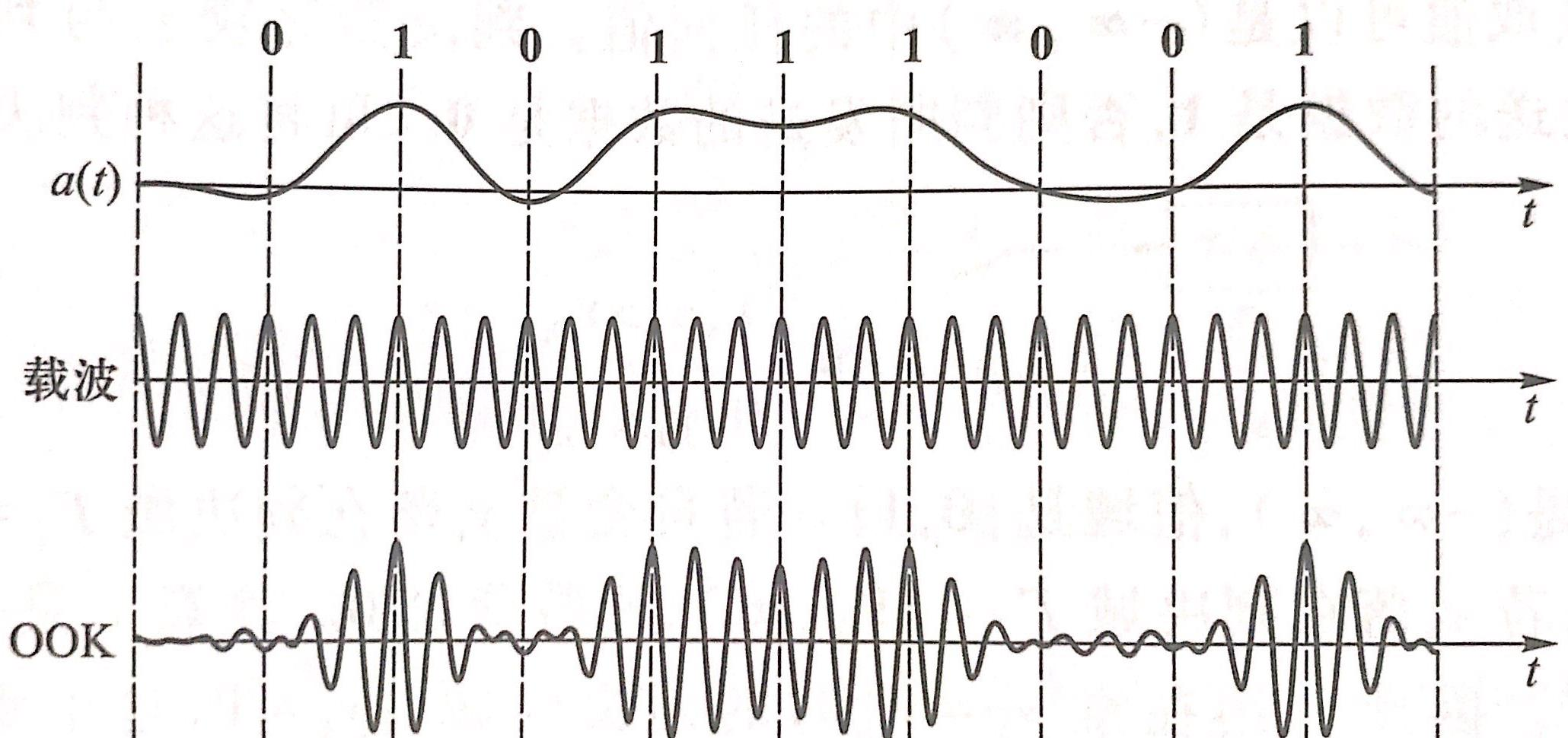
功率谱如下:
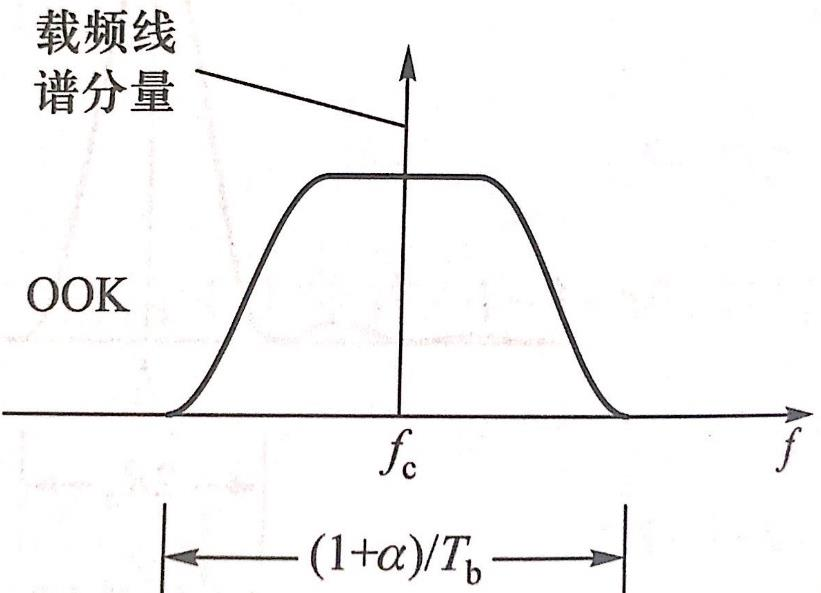
看着是不是顺眼多了。其带宽为 \[ \frac{1+\alpha}{T_b} \] 里面的\(\alpha\)是根升余弦滤波器的滚降因子。频谱效率为\(1/(1+\alpha)\)
在解调时,因为是DSB信号,所以可以用DSB信号的解调方法,比如相干解调
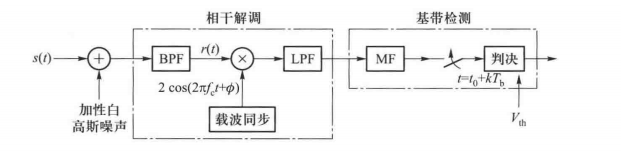
其中MF是匹配滤波器,如果\(g(t)\)是矩形窗,那么MF是积分清零器。
B点基带输入信号、噪声功率谱密度与上一章匹配滤波器输入信号、噪声功率谱密度完全一致,C点判决误符号率为 \[ p_s=Q\left(\frac A{\sqrt{n_0/2}}\right) \] 因为\(E_b=E_s=\frac 12(0+4A^2)\),所以 \[ p_b=Q\left(\sqrt{\frac{E_b}{n_0}}\right) \]
此外,还可以使用包络检波器进行非相干解调。非相干解调的误比特率比相干解调略高,信噪比差在匹配滤波上。
其余二进制调制
BPSK
对单极性非归零码进行相位调制,得到BPSK信号,框图如下:
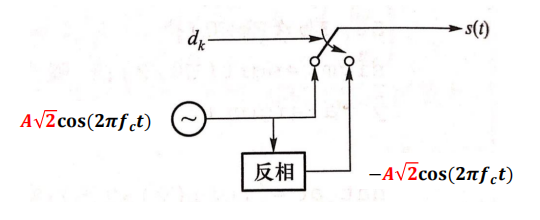
信号表达式为: \[ s(t)=A\sqrt 2cos [2\pi f_ct+\pi a(t)] \] 其波形是在两种相反的相位(\(0,\pi\))之间切换的正弦波,即:
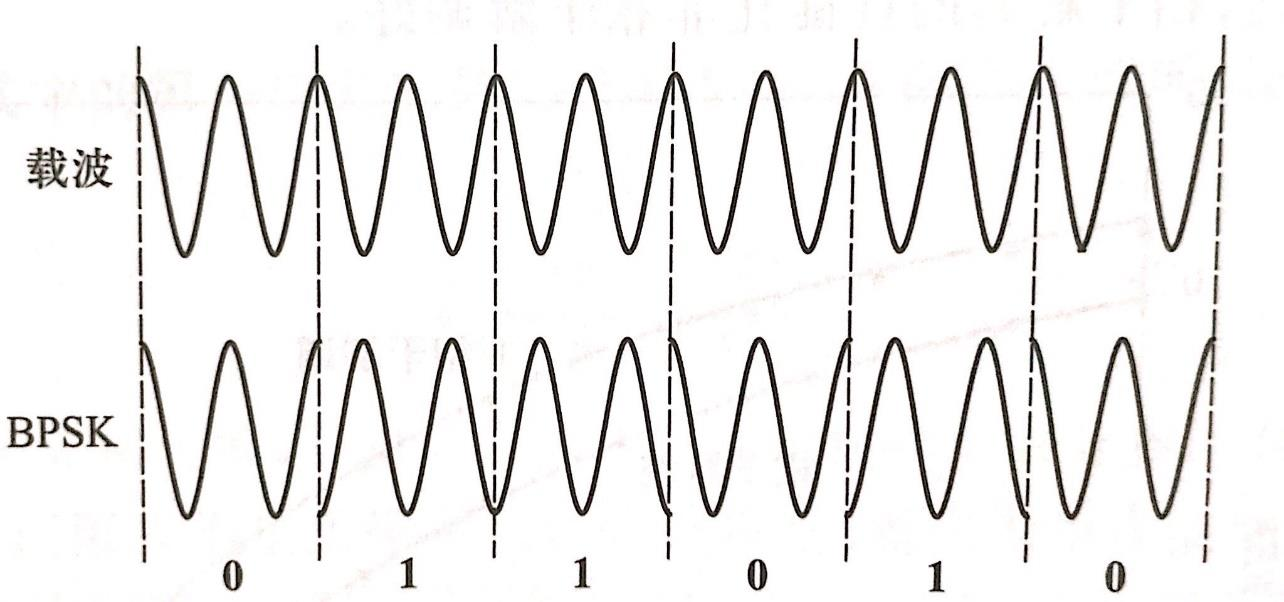
它也可以理解为一个DSB信号,即:
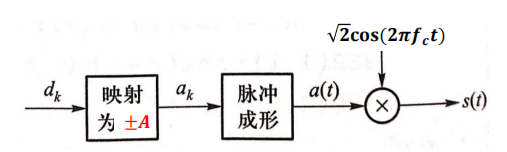
它和前面的OOK都是2ASK,不过其中一个的幅度是\(\{0,A\}\),而另一个是\(\{-A,A\}\)
与OOK相比,其功率谱中没有冲击分量,其余的形状和参数基本类似。
在解调上,包络检波器显然是不能用了,所以只能相干解调。输出判决误符号率是 \[ p_s=Q\left(\frac A{\sqrt{n_0/2}}\right) \] 但是因为\(E_b=E_s=\frac 12 (A^2+A^2)\),所以: \[ p_b=Q\left(\sqrt{\frac{2E_b}{n_0}}\right) \] 在相同\(E_b/n_0\)的条件下,BPSK的误比特率比OOK更低.
二进制频移键控2FSK
把单极性非归零码进行FM调制,就得到2FSK。
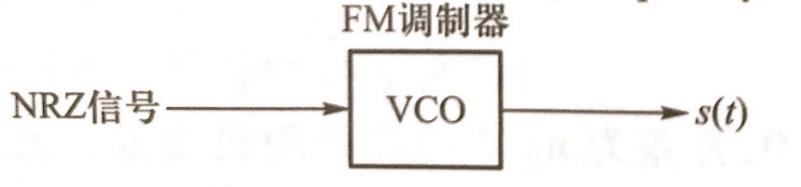
信号表达式为: \[ s(t)=A \sqrt{2} \cos \left[2 \pi f_c t+2 \pi K_{F M} \int_{-\infty}^t a(\tau) d \tau\right] \] 波形如下:
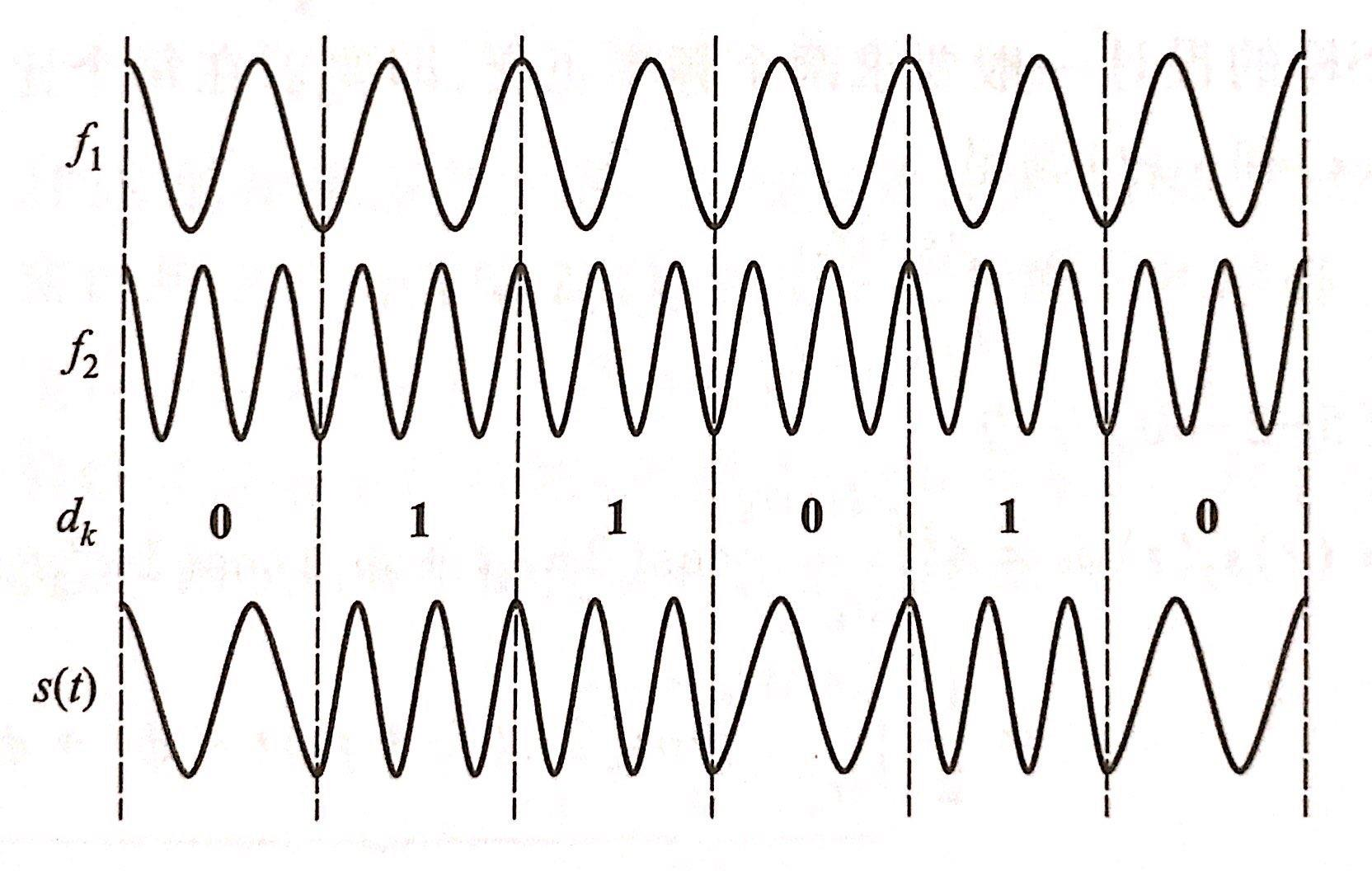
当然,如果至少为了实现频率切换,其实还有更方便的方法:
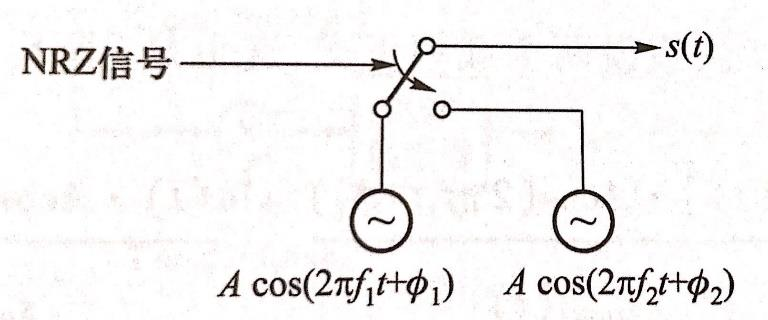
特别注意:这两个框图并不等价,主要差别在相位是否连续。第二个框图的表达式为 \[ s(t)=\left\{\begin{array}{l} s_1(t)=A \sqrt{2} \cos \left(2 \pi f_1 t+\phi_1\right), a(t)=0 \\ s_2(t)=A \sqrt{2} \cos \left(2 \pi f_2 t+\phi_2\right), a(t)=1 \end{array}\right. \] 波形如下:
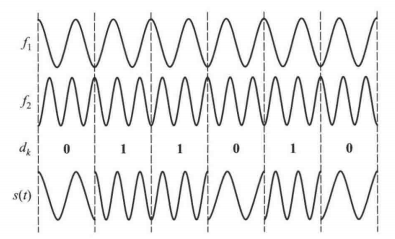
在实践中,一般要求这两个载波信号相互正交,具体来说,就是: \[ \frac{1}{T_s} \int_{k T_s}^{(k+1) T_s} s_1(t) s_2(t) d t=0 \] 满足要求的最小频差为\(1/2T_b\)
对于上面的那个表达式,可以改写为: \[ s(t)= {[1-a(t)] A \cdot \sqrt{2} \cos \left(2 \pi f_1 t+\phi_1\right)+}a(t) A \cdot \sqrt{2} \cos \left(2 \pi f_2 t+\phi_2\right) \] 这就是两个OOK之和
所以它的功率谱密度也是两个OOK之和,即:
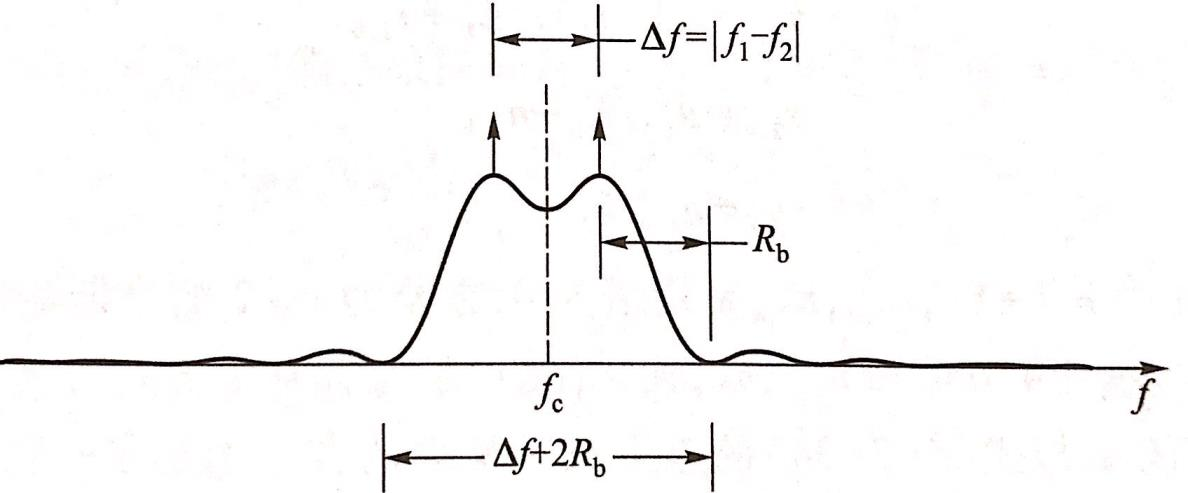
主瓣带宽为\(2R_b+\Delta f\)
2FSK一般不用根升余弦脉冲来改善旁瓣,因为这是因为2FSK系统具有恒定的包络,而根号升余弦脉冲成形后的信号包络不是常数(恒包络调制容易实现高发射功率)。
因为是两个OOK之和,所以既可以用相干解调,也可以用非相干解调,误比特率也和OOK一样,为: \[ p_b=Q\left(\sqrt{\frac{E_b}{n_0}}\right) \] 在相同\(E_b/n_0\)的条件下,2FSK和OOK有相同的抗噪声性能
但如果载波幅度𝐴相同,则OOK的平均比特能量比2FSK小一半,此时OOK的误比特率比2FSK高
二进制差分相移键控2DPSK
若将输入的比特序列先进行差分编码,然后进行BPSK调制,如下图所示,便形成了二进制差分相移键控.
波形如下:
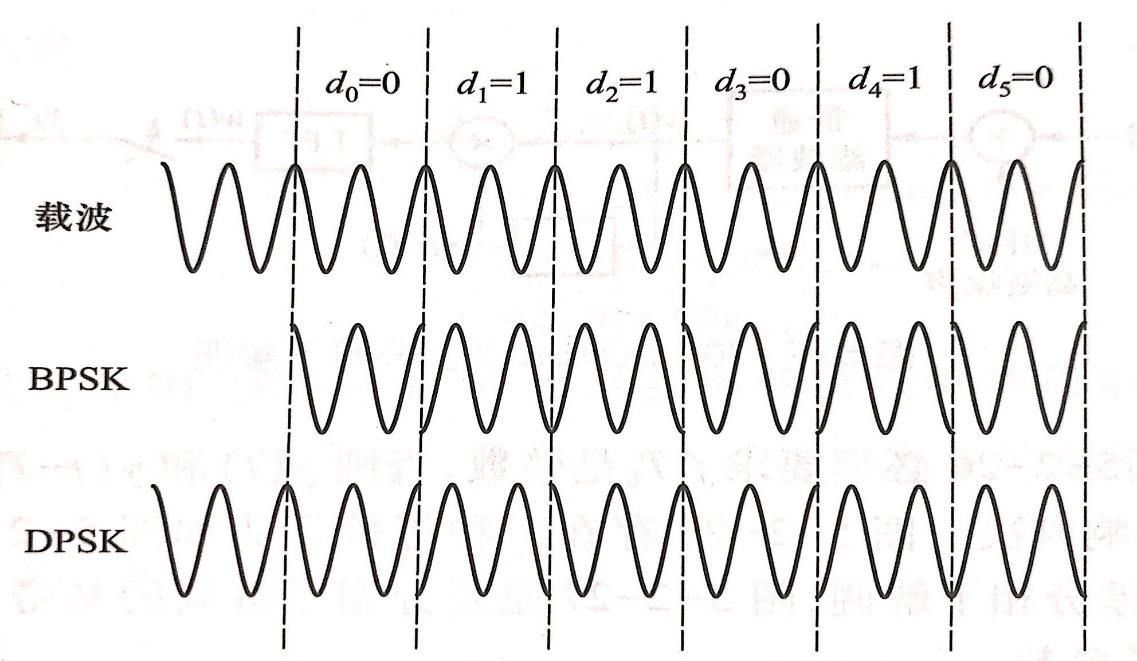
图中是传号差分,即\(d=0\)时相位不变,\(d=1\)时相位翻转。
因为2DPSK从本质上来说还是BPSK,所以可以相干解调。但是2DPSK信息携带在前后两个比特的已调信号相位差上,因此其解调也可以直接检测这个相位差。这种方法叫差分相干解调,如下图所示。因为不需要提取载波,故其属于非相干解调。
差分译码器的输出是 \[ \hat d_k=\hat c_k \oplus \hat c_{k-1} \] 所以2DPSK相干解调误比特率是 \[ P_s=P_b=2 Q\left(\sqrt{\frac{2 E_b}{n_0}}\right)\left[1-Q\left(\sqrt{\frac{2 E_b}{n_0}}\right)\right] \] 近似为BPSK的两倍,而且会出现误码传播情况。
直观看一下各个二进制调制的误比特率:
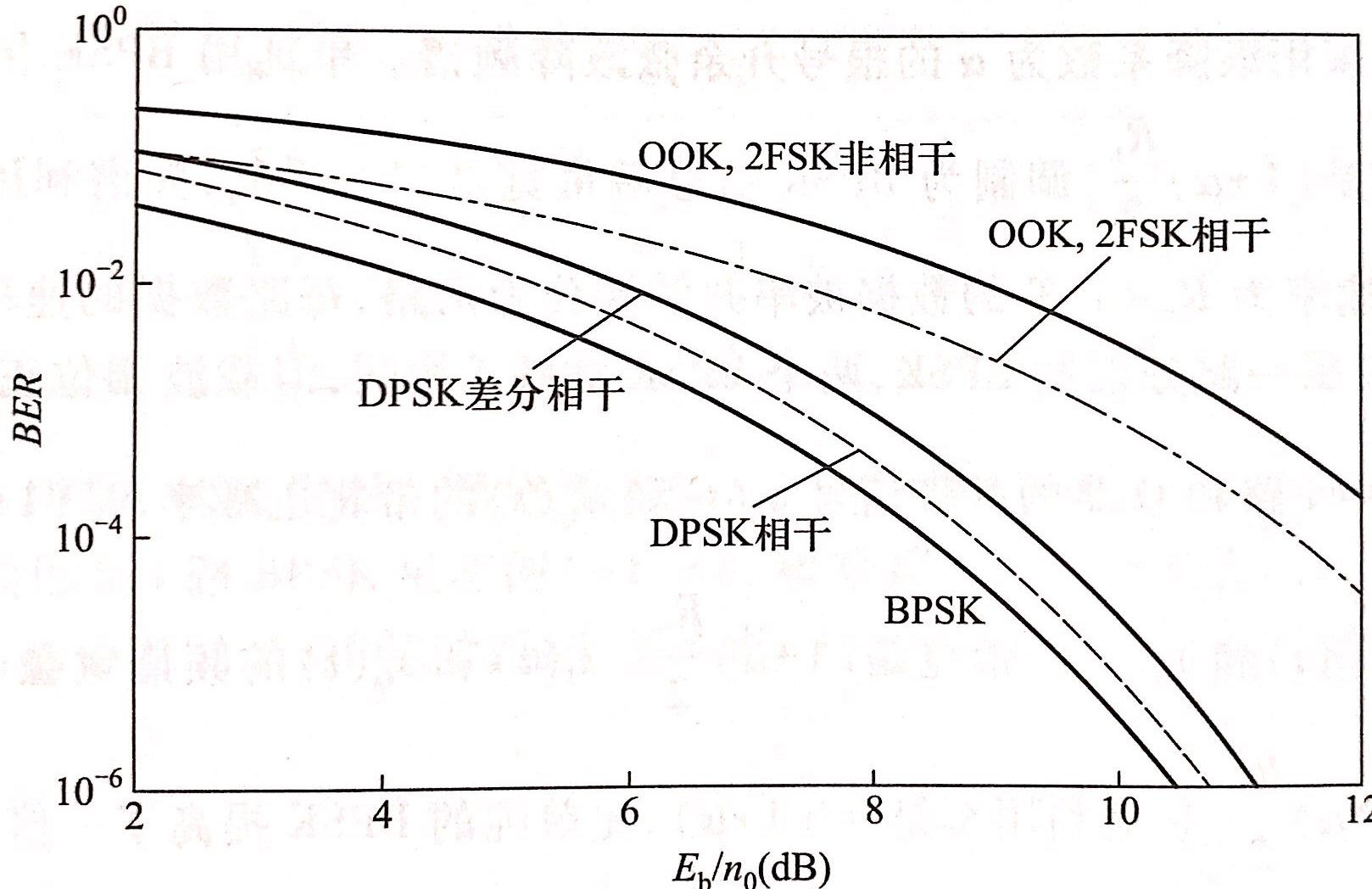
【例(2022期末)】某二进制数字信号码元传输速率是\(2\times 10^6baud\),分别采用2ASK、2PSK、2FSK系统传输,载波频率100MHz,FSK系统两个频率分别为\(f_1=95MHz,f_0=105MHz\),输入接收端解调器的信号振幅为\(A=40\mu V\),信道噪声是加性高斯白噪声,单边功率谱密度\(n_0=5\times 10^{-18} W/Hz\),求
- 2ASK、2PSK、2FSK频带宽度
- 相干接收时,2ASK、2PSK、2FSK误码率
【解】
频带宽带,有:\(BW_{ASK}=BW_{PSK}=2R_b=4MHz\)
\(BW_{FSK}=2R_b+\Delta f=14MHz\)
对2ASK:
\(P_1=\frac 12 A^2=8\times 10^{-10}\),\(P_0=0\)
所以平均符号功率:\(P_s=\frac 12(P_1+P_0)=4\times 10^{-10}\)
时间为\(T_s=1/R_s=5\times 10^{-7}\)
则平均符号能量为\(E_s=P_sT_s=2\times 10^{-16}\)
代入 \[ P_e=Q\left(\sqrt{\frac{E_s}{n_0}}\right)=Q(2\sqrt{10}) \] 对2PSK:
\(P_s=\frac 12A^2=8\times 10^{-10}\)
时间为\(T_s=1/R_s=5\times 10^{-7}\)
则平均符号能量为\(E_s=P_sT_s=4\times 10^{-16}\)
代入: \[ P_e=Q\left(\sqrt{\frac{2E_s}{n_0}}\right)=Q(4\sqrt{10}) \] 对2FSK:
\(P_s=\frac 12A^2=8\times 10^{-10}\)
时间为\(T_s=1/R_s=5\times 10^{-7}\)
则平均符号能量为\(E_s=P_sT_s=4\times 10^{-16}\)
代入: \[ P_e=Q\left(\sqrt{\frac{E_s}{n_0}}\right)=Q(4\sqrt{5}) \]
正交相移键控QPSK
可在BPSK的基础上叠加另一个正交载波的BPSK,两个BPSK各传一半数据,如下图所示,这种方式称为正交相移键控(QPSK)
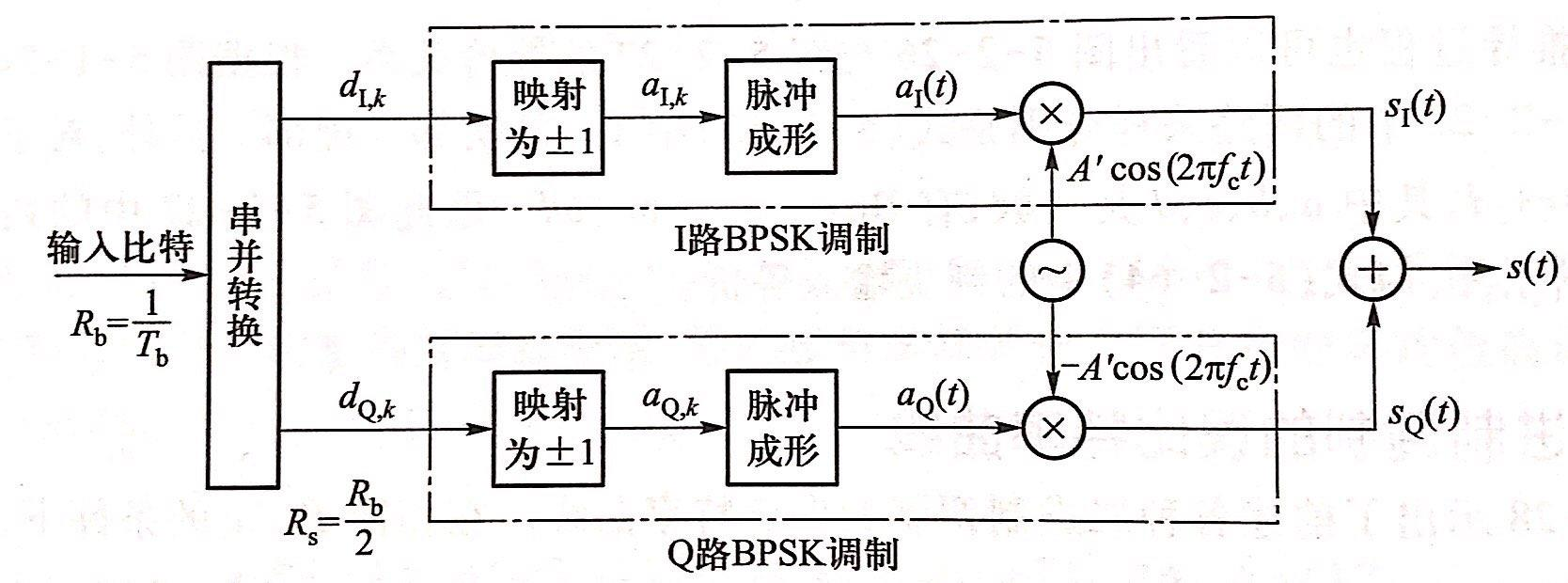
在QPSK中,因为数据被串并转换了,所以符号间隔\(T_s=2T_b\)。
发送单个符号\((a_{I,k},a_{Q,k})\)时QPSK的数学表达式为: \[ \begin{aligned} s(t)= \sqrt{2} A a_{I, k} g\left(t-k T_s\right) \cos \left(2 \pi f_c t+\phi\right)- \sqrt{2} A a_{Q, k} g\left(t-k T_s\right) \sin \left(2 \pi f_c t+\phi\right) \end{aligned} \] 化简得: \[ s(t)=2 g\left(t-k T_s\right) \cos \left(2 \pi f_c t+\phi+\theta_k\right) \] 其中信号控制的是\(\theta_k\),如下:
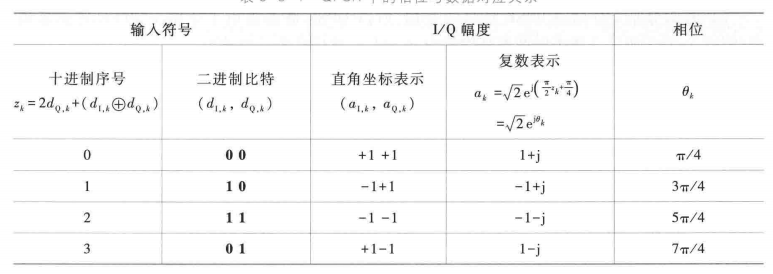
星座图为:
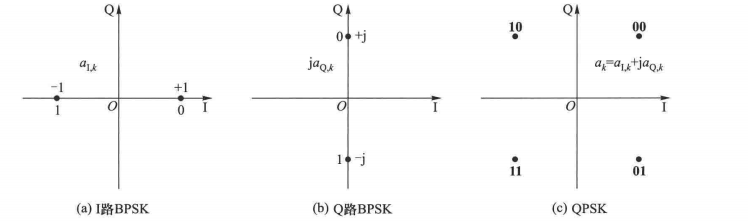
其功率谱密度是BPSK的两倍。
对QPSK的解调可以用I/Q两路BPSK解调器组合而成,每个BPSK的误比特率是 \[ p_b=Q\left(\sqrt{\frac{2E_b}{n_0}}\right) \] 所以QPSK的误符号率是 \[ p_s=1-(1-p_b)^2 \] 当信噪比较高时,误符号率近似是误比特率的2倍
OQPSK
在普通QPSK中,有时候会出现包络起伏比较严重的情况。为了降低包络起伏程度,可以把两路信号在时间上错开,错开零点,这就叫OQPSK
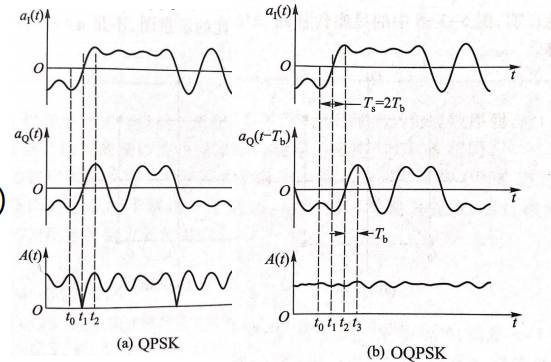
在发送端,将Q路的信号延迟\(T_b=T_s/2\)即可。其功率谱、误码率等和QPSK相同。
恒包络调制MSK
为了降低非线性失真的影响,希望数字调制的输出信号有较低的包络起伏。OQPSK就是为此目的提出的,它通过将Q路错开𝑇𝑏时间使包络的起伏显著减小。包络起伏最小的情况是无起伏,即包络是常数。包络是常数的调制称为恒包络调制。
在2FSK中,若FM调制的设计能使2FSK信号的两个频率的频差成为保持正交的最小间隔\(1/2T_s\),那就得到了最小频移键控MSK。
有: \[ s(t)==A \cos \left[2 \pi f_{\mathrm{c}} t+2 \pi K_{\mathrm{FM}} \int_{-\infty}^t a(\tau) \mathrm{d} \tau\right] \] 其相位有: \[ \frac{\mathrm{d}}{\mathrm{d} t} \varphi(t)=\frac{\pi}{2 T_{\mathrm{b}}} \cdot a(t)=\frac{\pi}{2 T_{\mathrm{b}}} \cdot \sum_{i=-\infty}^{\infty} b_i g\left(t-i T_{\mathrm{b}}\right) \] 其中\(a(t)\)是取值于\(\pm1\)的双极性NRZ信号,\(g(t)\)是持续时间为\([0,Ts]\),高度为1的矩形脉冲。\(b\in\{±1\}\)代表双极性NRZ信号所携带的二进制数据。
MSK是用FM形成的,而不是用开关形成的,相位是连续的,而且可以绘出相位路径:
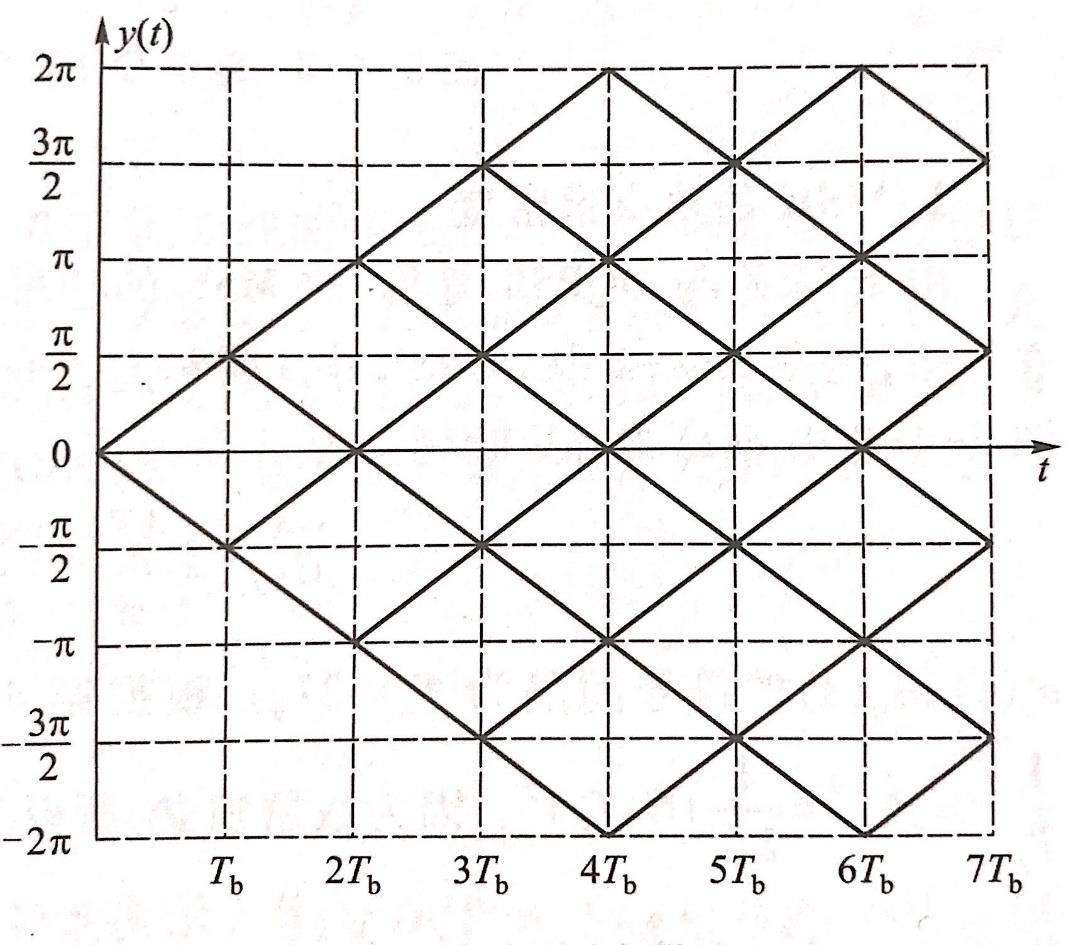
其在每一个比特间隔中都是连续线性变化,往上走还是往下走取决于\(b_i\)的取值。如果\(b_i\)是\(1\),那就是往上走,否则如果\(b_i=-1\)就是往下走。
事实上如果OQASK使用了一种特殊的成型脉冲:
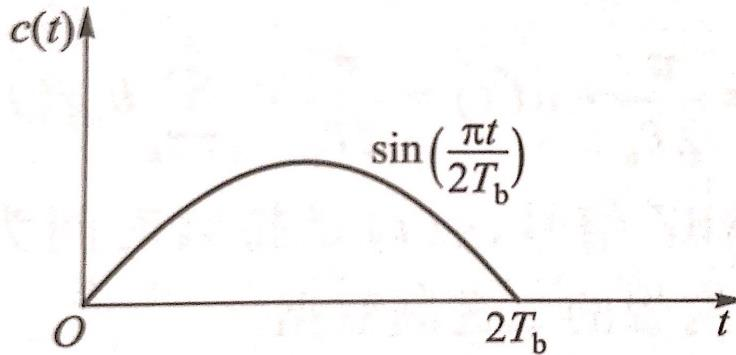
那它就是MSK。所以MSK的功率谱可以从OQPSK得到。
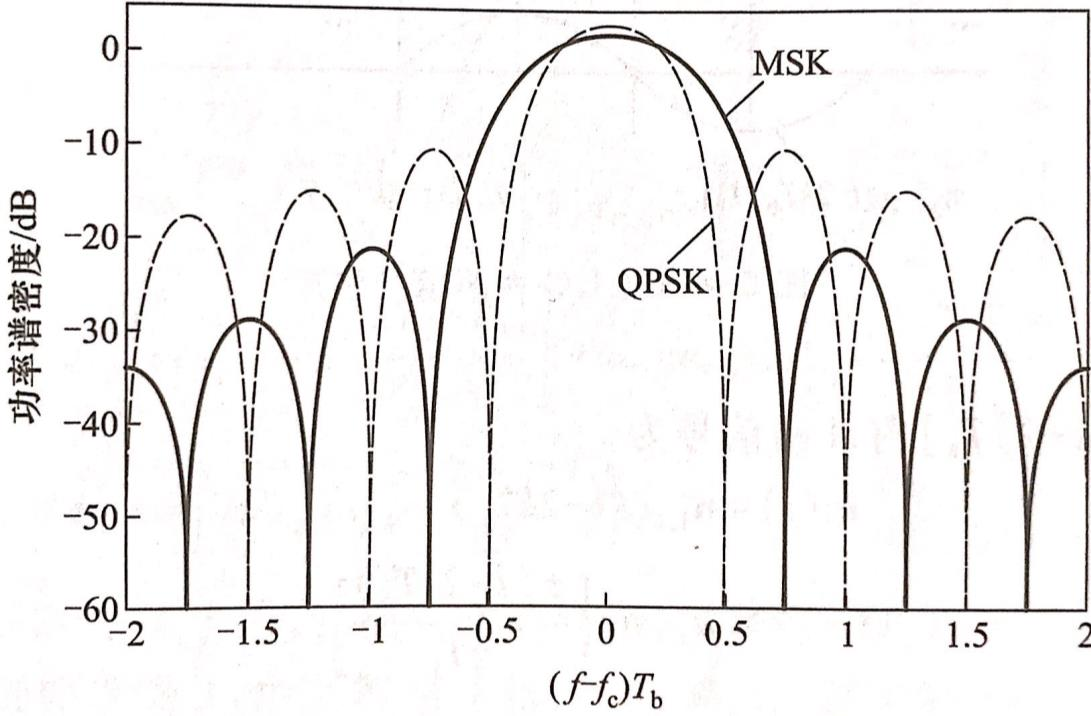
MSK的主瓣带宽是\(1.5/𝑇_𝑏\),QPSK的主瓣带宽是\(1/𝑇_𝑏\)
高阶调制
MASK
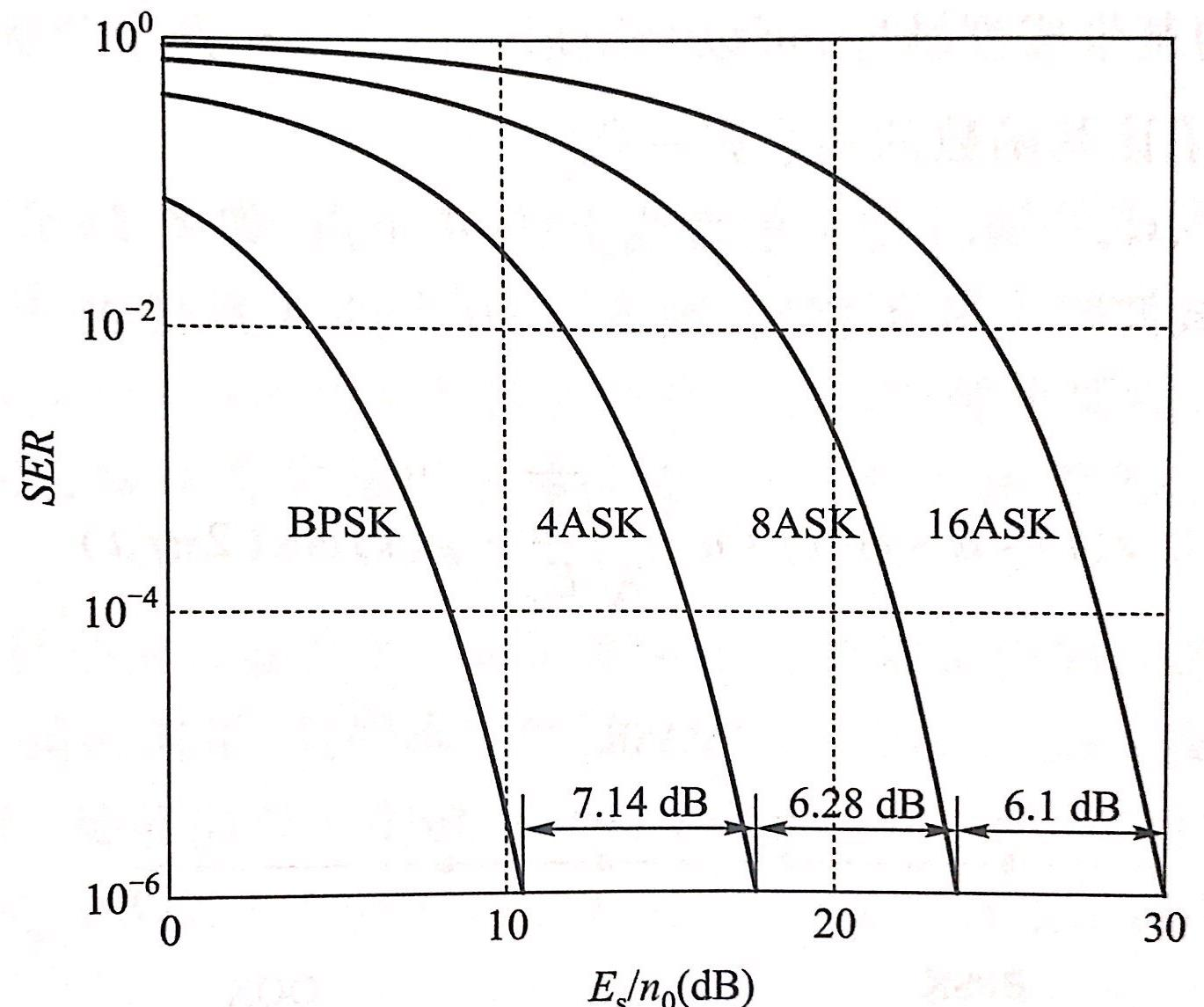
类比于2ASK,其中M是符号数。在功率谱上,双极性MASK信号与BPSK一致(没有线谱),单极性MASK信号与OOK一致(有线谱)。MASK的误符号率已经在“数字信号基带传输”里分析过了。
QAM
类似于用俩载波正交BPSK构成QPSK,也可以用俩载波正交ASK构成QAM。
MQAM是由两路\(\sqrt M\)ASK组成的:
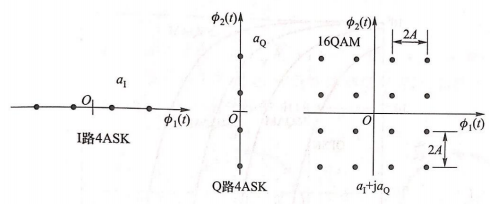
误符号率: \[ p_s=1-\left(1-p_{s, \mathrm{ASK}}\right)^2 \approx \frac{4(\sqrt{M}-1)}{\sqrt{M}} Q\left(\sqrt{\frac{3}{M-1} \frac{E_s}{n_0}}\right) \]
MFSK
MFSK的星座图是在M维欧氏空间的每个坐标轴上放一个点。
对某一个载频来说,开关时而接通,时而断开,形成一个OOK。因此可将MFSK信号看成是M个OOK信号的叠加。
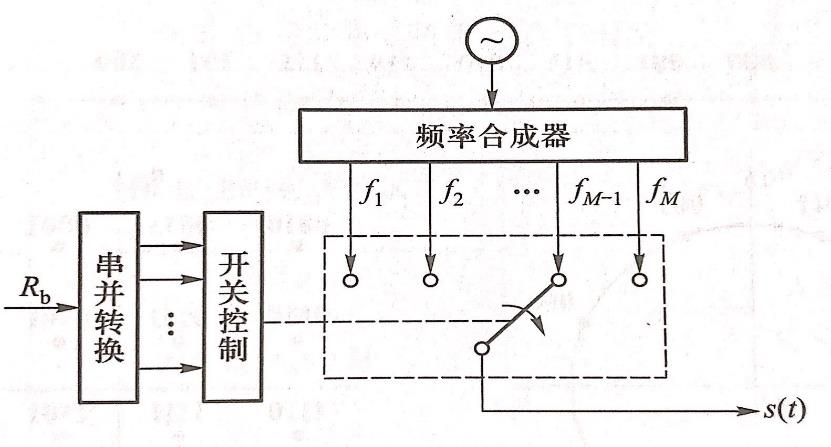
主瓣带宽为: \[ B=\left|f_M-f_1\right|+2 R_s \] 在频差按最佳设计的情况下,相邻载波的频差是1/(2𝑇𝑠 )=𝑅𝑠/2,主瓣带宽为 \[ B=\frac{M-1}{2} R_s+2 R_s=\frac{M}{2} R_s+1.5 R_s \]
MPSK
MPSK的星座分布在圆上
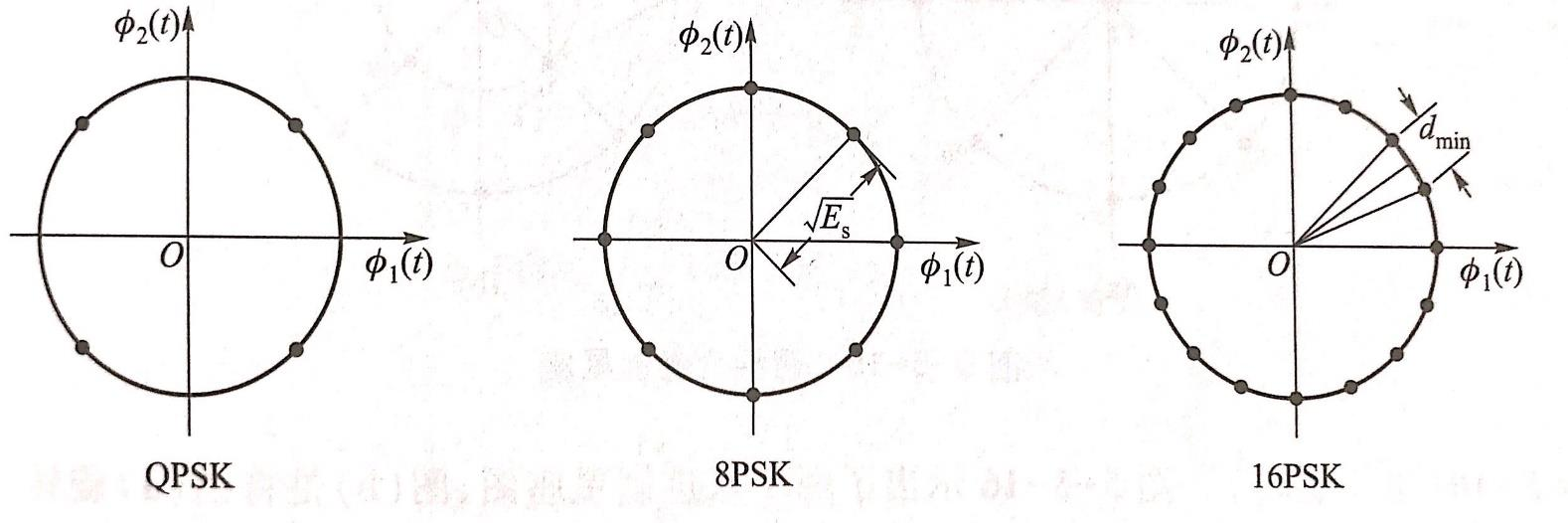
差错控制编码
在实际信道上传输数字信号时,由于信道传输特性不理想及加性噪声的影响,接收端所收到的数字信号不可避免地会发生错误。为了在给定信噪比情况下达到一定的误比特率指标,应该合理设计基带信号,选择调制解调方式,采用时域、频域均衡,使误比特率尽可能降低。但若误比特率仍不能满足要求,则必须采用信道编码(即差错控制编码),将误比特率进一步降低。
差错控制的基本思路是:在发送端给被传送的信息附带一些冗余的监督码元,这些监督码元和信息码元之间以某种规则建立联系,然后在接收端检验收到的信息是否符合这样的联系,如果不符合,那么就可以断定传输中出现了错误。
常用的差错控制方式主要有三种:检错重发(实时性不好),前向纠错(效率高,实时性好,可靠性低),混合ARQ。其中检错重发又有停发等候重发、返回重发、选择重发。
检错和纠错的基本原理
之前已经说了差错控制的基本思路,接下来举例说明一下。
比如三位二进制码共有八种,即:000,001,010,011,100,101,110,111
如果都用来传递信息,那么不能检错。
但是如果只使用四个码000,011,101,110,其中前两位是要传递的信息,而最后一位是前两位的模2和,其它四个码是禁用码字。如果接收端接收到了禁用码字,那么就可以断言传输过程中出现了错误。这就是检错的过程。
在信道编码中,定义码组中非零位的数目为码组的重量,简称码重。
把两个码组中对应码位上具有不同二进制位的位数定义为两码组的距离,称为汉明距,简称码距。
如果要在一个码组内检测\(e\)个误码,要求最小码距 \[
d_{min}\geq e+1
\] 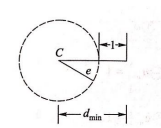
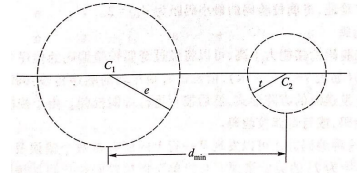
如图所示,如果误码个数不超过\(e\),则说明码组的位置移动不会离开半径为\(e\)的多维球中。这意味着其它码组必须位于以\(C\)为圆心,以\(e+1\)为半径的圆上或圆外。
如果要在一个码组内纠正\(t\)个误码,要求最小码距 \[ d_{min}\geq 2t+1 \] 示意图如下:
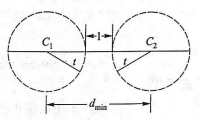
只要这两个码字的移动范围不相交,那么就可以进行纠正。
如果要在一个码组内纠正\(t\)个误码,同时检测\(e\)个误码,则要求最小码距 \[ d_{min}\geq t+e+1 \] 示意图如下:
线性分组码
将信息码分组,为每组信息位附加若干监督位,且信息位和监督位间的关系可由线性方程组表示的编码,称为线性分组码。这些码字构成一个群,性质有:
- 任意两个码字的逐位模2和仍然是码字
- 码的最小距离等于非零码的最小重量
比如前面提到的奇偶校验码,就是一种最简单的线性分组码,其偶校验关系为: \[ a_0\oplus a_1\cdots a_{n-1}=0 \] 接收时,计算 \[ s=a_1+a_2+\cdots+a_{n-1} \] 这里的\(s\)称为校正子或者伴随式,如果\(s=0\)表示没有错误。
对于码总长为\(n\),信息位长度为\(k\),校验长度为\(r=n-k\)的线性分组码,一般记作\((n,k)\)线性分组码。例如上面的奇偶校验码就是\((n,n-1)\)线性分组码。如果满足\(2^r-1\geq n\),则有可能构造出纠正一位甚至更多错误的分组码。
下面通过一个更加一般的例子来说明如何构造线性分组码。设\((n,k)\)分组码中\(n=7\),要求校正一位错误,则\(r\geq 3\)。现取\(r=3,k=4\),即为\((7,4)\)分组码。用\(a_0a_1a_2a_3a_4a_5a_6\) 表示一个码字,用\(s_1s_2s_3\)表示三个校正子,假设\(s_1s_2s_3\)和误码位置的关系如下表:
| s1s2s3 | 误码位置 | s1s2s3 | 误码位置 |
|---|---|---|---|
| 001 | a0 | 101 | a4 |
| 010 | a1 | 110 | a5 |
| 100 | a2 | 111 | a6 |
| 011 | a3 | 000 | 无误码 |
先看\(s_1\),当误码位置为\(a_2,a_4,a_5\)或\(a_6\)时,\(s_1=1\),因此,有: \[ s_1=a_2+a_4+a_5+a_6 \] 如法炮制,对\(s_2\)有: \[ s_2=a_1+a_3+a_5+a_6 \] 对\(s_3\)有: \[ s_3=a_6+a_4+a_3+a_0 \] 假设\(a_3a_4a_5a_6\)是用来承载信息的位,\(a_0a_1a_2\)是校验位,则有: \[ \begin{cases} a_6+a_5+a_4+a_2=0\\ a_6+a_5+a_3+a_1=0\\ a_6+a_4+a_3+a_0=0 \end{cases} \] 移项一下,就是: \[ \left\{\begin{array}{l} a_2=a_6+a_5+a_4 \\ a_1=a_6+a_5+a_3 \\ a_0=a_6+a_4+a_3 \end{array}\right. \] 由此可以生成16个许用码字:
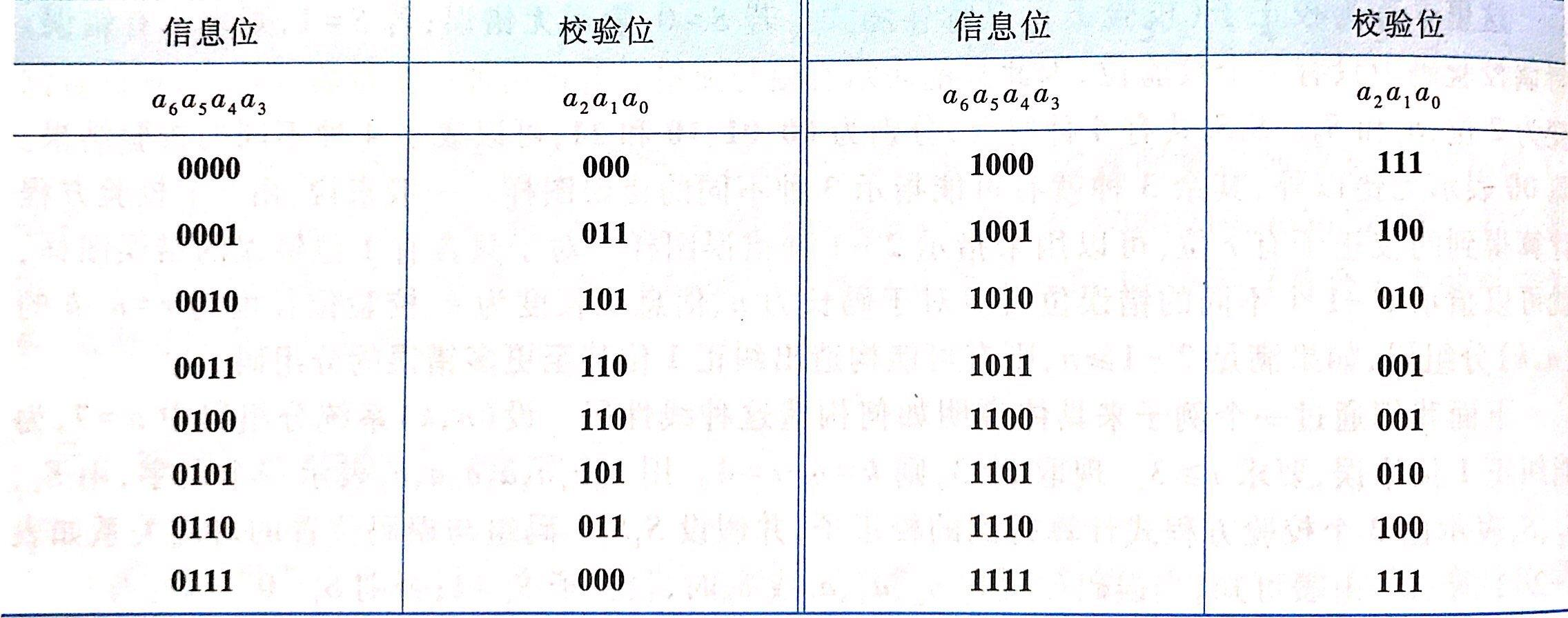
如果把检验方程式写成比较完整的形式,有: \[ \left\{\begin{array}{l} 1 \cdot a_6+1 \cdot a_5+1 \cdot a_4+0 \cdot a_3+1 \cdot a_2+0 \cdot a_1+0 \cdot a_0=0 \\ 1 \cdot a_6+1 \cdot a_5+0 \cdot a_4+1 \cdot a_3+0 \cdot a_2+1 \cdot a_1+0 \cdot a_0=0 \\ 1 \cdot a_6+0 \cdot a_5+1 \cdot a_4+1 \cdot a_3+0 \cdot a_2+0 \cdot a_1+1 \cdot a_0=0 \end{array}\right. \] 写成矩阵形式,有: \[ \left[\begin{array}{lllllll} 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{lllllll} a_6 & a_5 & a_4 & a_3 & a_2 & a_1 & a_0 \end{array}\right]^T=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right] \] 即: \[ Ha=0 \]
这里的\(r\times n\)矩阵\(H\)称为校验矩阵,信息位与校验位之间的校验关系完全由\(H\)决定。矩阵中元素1表示相应位之间存在偶校验关系. \[ \mathbf{H}=\left[\begin{array}{llllllll} 1 & 1 & 1 & 0 & \vdots & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & \vdots & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & \vdots & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ll} \mathbf{P} & \mathbf{I}_r \end{array}\right] \] 其中\(P\)是\(r\times k\)阶矩阵,表示实际校验关系,而\(I\)是\(r\)阶单位阵,表示校验位是\(a_2a_1a_0\)这三位。具有上面形式的校验矩阵称为系统形式校验矩阵。
对于生成方程,也可以写出其矩阵形式: \[ \left[\begin{array}{lll} a_2 & a_1 & a_0 \end{array}\right]=\left[\begin{array}{llll} a_6 & a_5 & a_4 & a_3 \end{array}\right]\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{array}\right]=\left[\begin{array}{llll} a_6 & a_5 & a_4 & a_3 \end{array}\right] \mathbf{Q} \] 其中\(Q\)是\(k\times r\)矩阵,是\(P\)的转置。如果给\(Q\)的左边加上一个\(k\)阶单位阵,那么就形成了一个新的矩阵\(G\),这个\(G\)叫做“生成矩阵” \[ \mathbf{G}=\left[\begin{array}{ll} \mathbf{I}_k & \mathbf{Q} \end{array}\right]=\left[\begin{array}{lllllll} 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \end{array}\right] \] 那么如何利用生成矩阵生成码字呢?有: \[ \mathbf{a}^T=\left[\begin{array}{llll} a_6 & a_5 & a_4 & a_3 \end{array}\right] \mathbf{G} \]
【例】某\((n,k)\)线性分组码的监督(校验)矩阵是: \[ H=\left[\begin{array}{lllllll} 1 & 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 1 \end{array}\right] \]
- 求\(n,k\)
- 求生成矩阵
- 现在要传输信息
110,请写出生成码字- 假设接收到了
B=1000011,请纠正【解】
因为\(H\)是\(4\times 7\)矩阵,所以\(n=7,k=n-r=3\)
因为 \[ H=[P\quad I_4] \] 所以 \[ Q=P^T=\left[\begin{array}{lll} 1&1 & 1 & 0 \\ 0&1 & 1 & 1 \\ 1&1 & 0 & 1 \end{array}\right] \] 所以 \[ G=[I_k Q]=\left[\begin{array}{lllllll} 1 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 0 & 1 \end{array}\right] \]
当信息为
110时,有: \[ A=[110]G=[1101001] \] 所以信息是1101001由校正子: \[ S=BH^T=(1000011)\left[\begin{array}{llll} 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]=(1101) \] 因为 \[ S=EH^T \] 得校正子为
0010000,所以纠错后的码字为1010011
汉明码
汉明码是最早发现,最知名的分组码之一。它有以下特点:
- 码长\(n=2^m-1\)
- 信息码位\(k=2^m-m-1\)
- 校验码位:\(r=n-k=m\)
根据系统需要,有时有必要对现有的码进行修改,使其码长、信息位数目等参数的取值更为灵活,以提高实用性。对码进行修改的方法有多种,最常用的是码的扩展与缩短,从而得到扩展码和缩短码
如果要加上一位对所有位进行整体校验的校验位,则汉明码变成\((2^m,2^m-m-1)\)扩展汉明码,这会在校验矩阵\(H\)的最右侧添加一列全0,然后在最上面(或者最下面)添加一行全1。此时信息位数目不变但是校验位数目增大,能够纠正的错误图样也会增大。
除了扩展,也可以通过删除信息位的方式来提升纠错能力。如果把\(H\)矩阵最左侧的\(s\)列删除,则相当于把\(G\)矩阵中的左侧的单位阵删除\(s\)列,然后把这些列中非零元对应的行也一并删除。示意图如下:
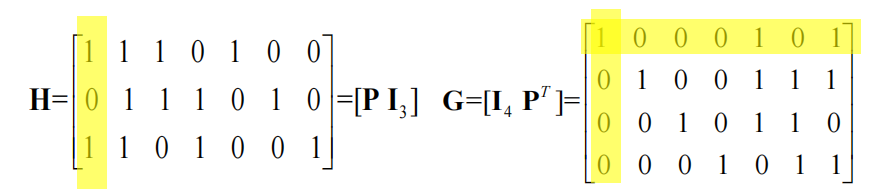 、
、
循环码
循环码是一种满足任何许用码字经过循环移位一行的码字还是许用码字的线性分组码,同样具有线性分组码的封闭性。
为了用代数学理论研究循环码,可将码字用多项式来表示,称为码多项式。码字\(A=\left(a_{n-1} a_{n-2} \cdots a_1 a_0\right)\)可表示为 \[ A(D)=a_{n-1} D^{n-1}+a_{n-2} D^{n-2}+a_{n-3} D^{n-3}+\cdots+a_1 D+a_0 \] 这里的\(D\)叫做哑元,它本身没什么意义,但是它的幂次很有意义。
那么如果把码字向左循环移位记作\(A^{(i)}\),那么: \[ A^{(i)}(D) \equiv D^i A(D) \quad \bmod \quad\left(D^n+1\right) \] 对于二元码,码多项式的系数只能从0和1中选取。0和1组成一个集合,并在该集合中定义两种运算:加法和乘法,运算规则如下:
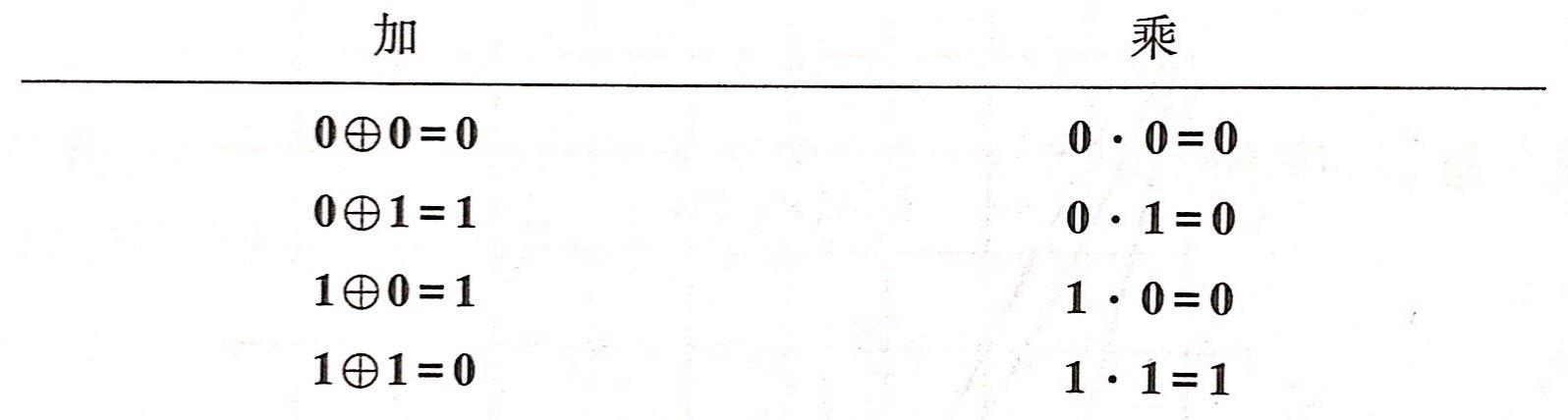
\(\{0,1,\oplus,\times\}\)构成一个代数系,称为二元域,它是最小的有限域(伽罗华域),记作\(GF(2)\)
循环码完全由其码长\(𝑛\)及生成多项式\(𝑔(𝐷)\)所决定.\(g(D)\)是一个能整除\(D^n+1\)的\(r=n-k\)阶多项式,也就是说,\(g(D)\)是\(D^n+1\)的一个因式。所有阶数低于\(n\)并且能被\(g(D)\)整除(即:是\(g(D)\)的倍式)的多项式就构成一个\((n,k)\)循环码。
例如,对于\((7,3)\)循环码,\(g(D)=D^4+D^3+D^2+1\)是\(D^7+1\)的一个因子,有: \[ \begin{aligned} 0&=g(D) \cdot 0 \\ D^4+D^3+D^2+1&=g(D) \cdot 1 \\ D^5+D^4+D^3+D&=g(D) \cdot D \\ D^6+D^5+D^4+D^2&=g(D) \cdot D^2 \\ D^5+D^2+D+1&=g(D) \cdot(D+1) \\ D^6+D^3+D^2+D&=g(D) \cdot\left(D^2+D\right) \\ D^6+D^5+D^3+1&=g(D) \cdot\left(D^2+1\right) \\ D^6+D^4+D+1&=g(D) \cdot\left(D^2+D+1\right) \\ \end{aligned} \] 那么这八个多项式就构成一个有八个码组的\((7,3)\)循环码。
循环码的生成矩阵,可以很容易地由生成多项式得到。先写出多项式矩阵 \[ G(D)=\left[\begin{array}{c} D^{k-1} g(D) \\ D^{k-2} g(D) \\ \vdots \\ D^0 g(D) \end{array}\right] \] 因为 \[ A(D)=M(D)G(D) \] 对应于前面的 \[ a^T=a_c^TG \] 所以对应的生成矩阵就是 \[ \mathbf{G}=\left[\begin{array}{lcccccc} g_{n-k} & g_{n-k-1} & \cdots & g_0 & 0 & \cdots & 0 \\ 0 & g_{n-k} & g_{n-k-1} & \cdots & g_0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & g_{n-k} & g_{n-k-1} & \cdots & g_0 \end{array}\right] \] 这是一个循环移位矩阵。可以看出,这个矩阵很可能不是系统形式矩阵,因为左边不一定是单位阵。系统码码字的最左\(k\)位是信息位,随后是\(r=n-k\)位校验位,也就是说码多项式是 \[ A(D)=M(D)D^{n-k}+r(D) \] 这里 \[ r(D)=r_{n-k-1} D^{n-k-1}+\cdots+r_0 \] 是校验多项式。那么\(A(D)\)能被\(g(D)\)整除的条件就是 \[ r(D)=M(D) D^{n-k} \bmod g(D) \] 于是,构造系统循环码的步骤是先把信息多项式乘以\(D^{n-k}\),然后对\(g(D)\)求余生成校验多项式,然后链接在一起。
系统形式的生成矩阵\(G=[I_k\quad Q]\),每行对应的信息多项式为\(m_i(D)=D^{k-i}\)
对应的校验多项式是 \[ r_i(D)=D^{n-i}\bmod g(D) \] 因此系统循环码生成矩阵多项式的一般表示为 \[ G(D)=\left[\begin{array}{c} A_1(D) \\ A_2(D) \\ \vdots \\ A_k(D) \end{array}\right]=\left[\begin{array}{c} D^{n-1}+r_1(D) \\ D^{n-2}+r_2(D) \\ \vdots \\ D^{n-k}+r_k(D) \end{array}\right] \] 对于所有线性分组码,非系统形式的生成矩阵经过高斯消元(初等行变换)运算也一定能够可以化为系统形式.
循环码的编码器可以用带反馈的线性移位寄存器来实现,如下图所示,以\(g(D)=D^6+D^5+D^4+D^3+1\)为例:
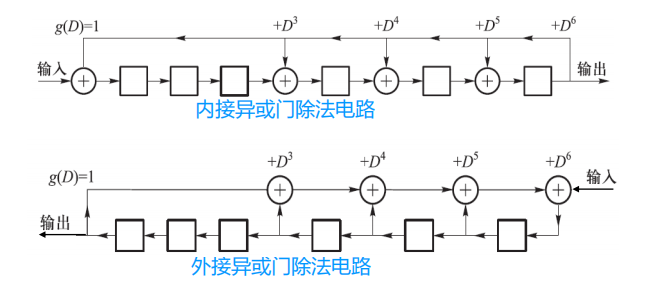
生成多项式哪一项有值,就在寄存器的第几个模块的后面增加一个异或门,这就是内接异或门触发电路的构成方法。
循环码的译码主要分三步进行:
由接收到的码多项式𝐵(𝐷)计算校正子(伴随式)多项式𝑆(𝐷): \[ S=BH^T \] 对于循环码来说: \[ S(D) \equiv B(D) \bmod g(D) \equiv E(D) \bmod g(D) \] 因此,循环码的校正子多项式\(S(D)\)就是用接收到的码多项式除以生成多项式\(g(D)\)所得到的余式
由校正子多项式\(S(D)\)确定错误图样\(E(D)\)
将错误图样\(E(D)\) 与\(B(D)\)相加,纠正错误
【例】已知\((7,4)\)循环码的生成多项式是\(g(D)=D^3+D+1\),求:
- 系统生成矩阵
- 系统监督矩阵
- 信息码为
1101,请编码【解】
有多项式矩阵: \[ G(x)=\left[\begin{array}{c} x^3 g(x) \\ x^2 g(x) \\ x g(x) \\ g(x) \end{array}\right]=\left[\begin{array}{c} x^6+x^4+x^3 \\ x^5+x^3+x^2 \\ x^4+x^2+x \\ x^3+x+1 \end{array}\right] \] 即: \[ G=\left[\begin{array}{l} 1011000 \\ 0101100 \\ 0010110 \\ 0001011 \end{array}\right] \] 经矩阵初等行变换,即给第一行加第三行和第四行,给第二行加第四行,有: \[ G=\left[\begin{array}{l} 1000101 \\ 0100111 \\ 0010110 \\ 0001011 \end{array}\right] \]
由\(H=[PI_r]\),有: \[ \mathbf{H}=[\mathbf{P} \mathbf{I} _r]=\left[\begin{array}{l} 1110100 \\ 0111010 \\ 1101001 \end{array}\right] \]
\(A=MG\)=
1101001
分组码的误码性能
下面仅就二进制对称信道及加性白色高斯噪声信道的情形,对一些常用的线性分组码进行讨论。
二进制对称信道
意思即是把0误为1和把1误为0的概率一样,都是\(p_e\)的信道。(忘了的话去看信息论)
不加纠错的误字率: \[ P_w=\sum_{i=1}^n p(i, n)=\sum_{i=1}^n\left(\begin{array}{l} n \\ i \end{array}\right) p_e^i\left(1-p_e\right)^{n-i} \] 加了纠错以后,如果纠错能力是\(t\),误字率的上界: \[ P_{w c}\leq\sum_{i=t+1}^n\left(\begin{array}{l} n \\ i \end{array}\right) p_e^i\left(1-p_e\right)^{n-i} \] 注意看\(\Sigma\)符号的下面。
一般来说,对于译码后的误比特率取决于特定的码及译码器,可近似地有 \[ P_b \leq \sum_{i=t+1}^n \frac{i}{n}\left(\begin{array}{l} n \\ i \end{array}\right) p_e^i\left(1-p_e\right)^{n-i} \]
加性高斯白噪声信道
考虑BPSK,原始误码率为: \[ p_b=Q\left(\sqrt{\frac{2E_c}{n_0}}\right) \] 其中,\(E_c\)为单位调制符号能量,\(n_0\)为噪声单边功率谱密度。定义单位信息比特的能量为\(E_b\)。如果没有差错控制编码,本来应该是\(E_c=E_b\)的,所以前一节里面的BPSK误码率里面写的是\(E_b\)。但是现在有了差错控制编码,有: \[ E_b=E_c\frac nk \] 所以 \[ p_e=Q\left(\sqrt{\frac{2 E_b}{n_0} \frac{k}{n}}\right) \]
通信原理的笔记到这里就结束了。关于后面的同步、多址和复用,请收看:
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
