信息论笔记·信道和编码
离散信道及其容量
信道的分类
根据信道的输入输出特性,可以分为:
- 离散信道:输入输出空间都是离散的
- 连续信道:输入输出空间都是连续的
- 半连续信道:输入输出空间中一个是离散的,而另一个是连续的
- 波形信道:输入输出都是时间的实函数
根据信道的统计特性,可以分为:
- 恒参信道:统计特性不随时间变化
- 变参信道:统计特性随时间变化
根据信道的记忆特性,可以分为:
- 无记忆信道:信道输出仅仅和当前的输入有关
- 有记忆信道:信道的输出还和过去的输入有关
还有几种比较特殊的信道:
满足以下条件之一(其实三个条件等价)的信道称为无损信道,无损信道的输出完全由输入决定:
- 总存在输出符号集合\(b_1,\cdots b_k\),满足\(P(Y\in b_i|x=x_i)=1\)
- 对于所有的输入分布,只要\(p(y_j)\neq 0\),则总有一个\(x_i\)使得\(p(x_i|y_j)=0\)
- 对于所有的输入分布,已知\(Y\)时,\(X\)的不确定度为零,即\(H(X|Y)=0\)
满足以下条件之一(其实两个条件等价)的信道称为无噪信道,无噪信道中不存在随机干扰:
- 对于所有的\(x_i\),都存在一个\(y_j\),使得\(p(x_i|y_j)=1\)
- \(H(Y|X)=0\)
既无损又无噪的信道叫做确定信道。
离散无记忆信道
首先来讨论单符号离散信道。假设信道输入随机变量(总体)为\(X\),其取值为\(x\), \(x\in A=\{a_1 ,a_2 ,……,a_r\}\);输出随机变量为\(Y\),取值为\(y\), \(y\in B={b_1 ,b_2 , ……,b_s }\)。信道传递概率为 \[ p(y|x)=P(Y=b_j|X=a_i)=p(b_j|a_i) \] 于是,可以用一个\(p\)组成的矩阵来描述这个信道,有: \[ \mathbf P=\begin{pmatrix} p_{11} & p_{12} & \cdots &p_{1s}\\ p_{21} & p_{22} & \cdots &p_{2s}\\ \cdots & \cdots & \cdots &\cdots\\ p_{r1} & p_{r2} & \cdots &p_{rs} \end{pmatrix} \] 其中\(p_{ij}=p(b_j|a_i)\)。这个矩阵的每个元素都大于等于零,而且行和都是\(1\)。
接下来介绍几个后面常用的名词,以免产生困扰:
先验概率:指的是信源的统计特性,即: \[ p(a_i)=p(X=a_i) \]
前向概率:即信道传递概率,也就是上面那个矩阵里面的元素,表示已经收到信源为\(a_i\)时信道输出\(b_j\)的概率,即 \[ p(b_j|a_i)=p(Y=b_j|X=a_i) \]
输出符号概率:指的是输出的统计特性,即: \[ p(b_j)=p(Y=b_j) \]
后向概率:指的是目前已经知道输出是\(b_j\),在这个情况下信源是\(a_i\)的概率,即: \[ p(a_i|b_j)=p(X=a_i|Y=b_j) \]
联合概率:指的是输入为\(a_i\)而且输出为\(b_j\)的概率,即: \[ p(a_ib_j)=p(X=a_i,Y=b_j) \] 有: \[ p(a_ib_j)=p(b_j)p(a_i|b_j)=p(a_i)p(b_j|a_i) \]
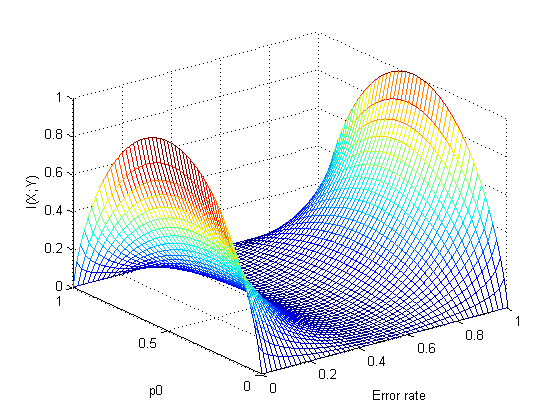
定义“信道疑义度”(损失熵)为: \[ \begin{aligned} H(X|Y) &= E[H(X|b_j)]\\ &= \sum_{j=1}^s p(b_j)\cdot \left(\sum_{i=1}^r-p(a_i|b_j)\log p(a_i|b_j)\right)\\ &= -\sum_{j=1}^s\sum_{i=1}^r p(a_ib_j)\log p(a_i|b_j) \end{aligned} \] 其物理意义为信宿收到全部符号Y后,对输入符号X尚存在的平均不确定程度。那么有:\(H(X|Y)\leq H(X)\),意思就是说,信宿接收到输出信号以后,总是要消除一些对信源的不确定度的。而平均互信息量就是来表征这一部分被消除的不确定度的: \[ I(X;Y)=H(X)-H(X|Y) \] 平均互信息量是输入信源概率分布的上凸函数,是信道传递概率\(p(y|x)\)的下凸函数。
无记忆扩展信道
对于单符号无记忆信道来说,输入和输出的都是一个符号。如果一个信道的输入是单符号信道的信源的N次扩展(也就是长度为N的序列),输出是单符号信道信宿的N次扩展,那么这个信道就是单符号信道的N次扩展信道。
在一般的信道中,传输长度为N的信息,有如下的定理:
如果输入和输出是\(N\)长序列\(\mathbf {X,Y}\),且信道是无记忆的,亦即信道传递概率为: \[ p(\mathbf{y} \mid \mathbf{x})=\prod_{i=1}^N p\left(y_i \mid x_i\right) \] 或者 \[ p\left(\beta_h \mid \alpha_k\right)=\prod_{i=1}^N p\left(b_{h_i} \mid a_{k_i}\right), k=1,2, \cdots, r^N, h=1,2, \cdots, s^N \] 则有: \[ I(\mathbf{X} ; \mathbf{Y}) \leq \sum_{i=1}^N I\left(X_i ; Y_i\right) \]
如果输入和输出是\(N\)长序列\(\mathbf {X,Y}\),且信源是无记忆的,即: \[ p(\boldsymbol{x})=\prod_{i=1}^N p\left(x_i\right) \] 或者 \[ p\left(\alpha_k\right)=p\left(a_{k_1}\right) p\left(a_{k_2}\right) \cdots p\left(a_{k_N}\right), k=1,2, \cdots, r^N \] 则: \[ I(\mathbf{X} ; \mathbf{Y}) \geq \sum_{i=1}^N I\left(X_i ; Y_i\right) \]
信道的组合
级联信道的模型如下:
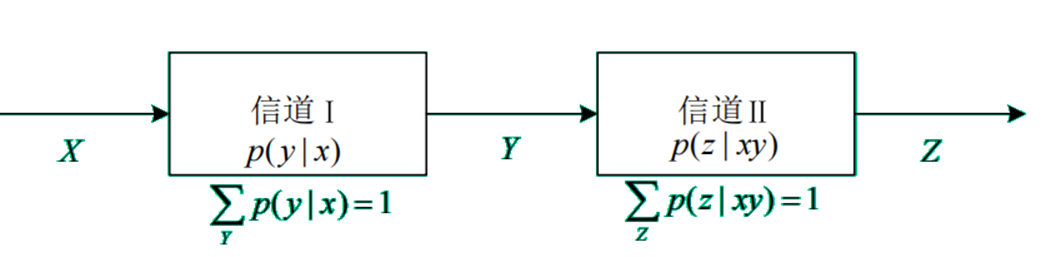
对于级联信道中的互信息,有:
级联信道中的平均互信息满足: \[ I(XY;Z)\geq I(Y;Z) \] 等号取得的充要条件: \[ p(z|xy)=p(z|y) \] 也就是说,输出变量\(z\)只和\(y\)有关,而和\(x\)无关。进一步,\(X,Y,Z\)构成了一个一阶马尔可夫链。
把上面两式右边的\(y\)换成\(x\),定理仍然成立。
如果\(X,Y,Z\)构成了一个一阶马尔可夫链,有: \[ I(X;Z)\leq I(X;Y) \]
\[ I(X;Z)\leq I(Y;Z) \]
也就是说,在任意信息传输系统中,最后获得的信息至多是信源提供的信息,如果在传输过程中丢失了信息,而且以后的系统不触及输入端,那么丢失的信息就不能再恢复。
信道容量
对一个特定的信道而言,其信道容量是平均互信息量随输入符号集变化时的最大值: \[ C=\max _{p(x)}\{I(X;Y)\} \] 相应的使得平均互信息量最大的信源概率分布称为最佳输入分布。信道容量\(C\)仅和信道本身的统计特性有关,而和信源无关,其表征了信道传送信息的最大能力。例如,对于最简单的二元对称信道(输入输出符号集都是\(\{0,1\}\),传输过程中符号翻转的概率为\(p\)),信源符号为\(1\)的概率是\(\omega\),有: \[ I(X;Y)=H(\omega \overline p+\overline \omega p)-H(p) \] 则: \[ C=1-H(p) \] 事实上,研究信道的核心问题就是研究信道容量以及最佳输入分布,但是这其实比较困难,接下来会对几个特殊的信道进行分析。
离散无噪信道
无损信道
无损信道的一个输入对应多个不相交的输出,输出端接收到\(Y\)以后一定能知道发射端\(X\)的状态,示意图如下:
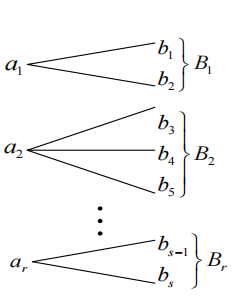
一个典型的无损信道矩阵如下: \[ \mathbf{P}_{Y \mid X}=\left[\begin{array}{cccccc} \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{6}{10} & \frac{3}{10} & \frac{1}{10} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \] 它的行“不相互重叠”,且行和为一。
其信道疑义度(损失熵)\(H(X|Y)=0\)。因为并不能根据输入\(a_i\)断定输出会是哪一个\(b_i\),所以其噪声熵\(H(Y|X)>0\)。其信道容量为: \[ C=\max _{p(x)}H(X)=\log r \] 最佳输入分布是等概分布。
确定信道
确定信道是一个输出对应多个互不相交的输入的信道,即发出信源\(a_i\),就一定能知道信道的输出\(b_j\)。示意图如下:
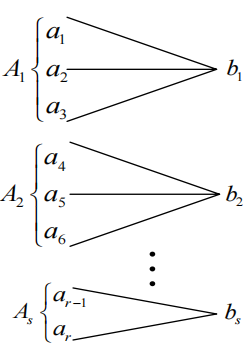
一个典型的确定信道矩阵如下: \[ \mathbf{P}_{Y \mid X}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \] 信道矩阵中每一行只有一个\(1\),其余元素都是\(0\)。
其噪声熵\(H(Y|X)=0\)。因为并不能根据输出\(b_j\)断定输入是哪一个\(a_i\),所以其损失熵\(H(X|Y)>0\)。
其信道容量为: \[ C=\max _{p(x)} H(Y)=\log s \] 最佳输入分布是能让输出呈现等概分布的输入分布。
无损确定信道
既无损又确定的信道是无损确定信道。其矩阵是单位阵,输入输出之间有一一对应关系。
离散对称信道
若一个离散无记忆信道的信道矩阵中,每一行都是其它行的同一组元素的不同排列,则称此类信道为离散输入对称信道,一个典型的离散输入对称信道矩阵为: \[ \mathbf{P}=\left[\begin{array}{cccc} \frac{1}{3} & \frac{1}{3} & \frac{1}{6} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{3} & \frac{1}{6} & \frac{1}{3} \end{array}\right] \] 若一个离散无记忆信道的信道矩阵中,每一列都是其它列的同一组元素的不同排列,则称此类信道为离散输出对称信道,一个典型的离散输出对称信道矩阵为: \[ \mathbf{P}=\left[\begin{array}{ll} 0.4 & 0.6 \\ 0.6 & 0.4 \\ 0.5 & 0.5 \end{array}\right] \] 如果同时满足以上两个条件,则称之为离散对称信道,例如: \[ \mathbf{P}=\left[\begin{array}{ccc} \frac{1}{2} & \frac{1}{3} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{2} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{6} & \frac{1}{2} \end{array}\right] \] 若一个离散无记忆信道,按照信道矩阵的行(即信道的输出集)可以将信道矩阵划分成\(n\)个子矩阵,且每个子矩阵中的每一行(列)都是其它行(列)的同一组元素的不同排列,则称此类信道为离散准对称信道。例如下面的矩阵: \[ \mathbf{P}_2=\left[\begin{array}{lll} 0.7 & 0.1 & 0.2 \\ 0.2 & 0.1 & 0.7 \end{array}\right] \] 可以划分为: \[ \left[\begin{array}{ll} 0.7 & 0.2 \\ 0.2 & 0.7 \end{array}\right]\left[\begin{array}{l} 0.1 \\ 0.1 \end{array}\right] \] 离散准对称信道的最佳输入分布是等概分布。
如果一个离散对称信道有\(r\)个输入符号和\(s\)个输出符号,则输入是等概分布时达到信道容量\(C\),且: \[ C=\log s-H\left(p_1^{\prime}, p_2^{\prime}, \cdots, p_s^{\prime}\right) \] 其中\(p'_1,p'_2,\cdots,p'_s\)是信道矩阵中的任何一行。
达到信道容量\(C\)的概率分布是使输出为等概分布的信道输入分布。求离散对称信道的信道容量,实质是求一种输入分布\(p(x)\),它使输出熵\(H(Y)\)达最大。对于对称信道,只有信道输入分布是等概分布时,输出才为等概分布。
对于离散无记忆 \(N\)次扩展信道,其信道容量等于单变量信道的信道容量的 \(N\)倍,即: \[ C^N=NC \]
无失真信源编码
将信源产生的全部信息无损地送给信宿,这种信源编码称无失真信源编码。编码可以分为:
- 定长码:所有码字长度相等的码
- 变长码:码字长度可能不相等的码
或者
- 奇异码:码组中有相同的码字
- 非奇异码:码组中没有相同的码字
分组码
分组码指的是把信源符号集中的每一个符号\(s_i\)都映射成一个固定的码字\(w_i\)的编码规则。
设信源符号\(s_i\)映射为一个固定的码字\(w_i\),则码\(\alpha_j=(s_{j_1},s_{j_2}\cdots s_{j_n})\)映射为\(W_j=(w_{j_1},w_{j_2},\cdots,w_{j_n})\)的分组码称为原分组码的\(N\)次扩展码。
分组码能正确译码的必要条件是非奇异,这很直观,但是并不是充分的。
如果一个分组码对于任意的正整数\(N\),其\(N\)次扩展码都是非奇异的,那么这样的分组码叫做唯一可译码,这是分组码能正确译码的充要条件。
虽然都是唯一可译码,但是译码方式仍有不同。考虑以下两种码:
| 符号 | 码1 | 码2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 10 | 01 |
| 3 | 100 | 001 |
| 4 | 1000 | 0001 |
对于码1来说,我接收到一个消息,比如10,此时我并不知道符号是2、3还是4。直到下一个符号到达,我接收到的消息变成101...,我才知道前面的符号是2。但是对于码2,当我接收到01时,我立刻就能知道这个符号是2。
把像码2这种接收到一个码字就能立刻译码的唯一可译码称为“即时码”。一个唯一可译码是即时码的充要条件是其中任何一个码都不是其它码的前缀。
定长码
唯一可译定长码
对于有\(q\)个符号的简单信源的\(N\)次扩展信源,其存在基本码符号数为\(r\),扩展信源\(S^N\)定长编码码长为\(L\)的唯一可译码的条件为: \[ q^N\leq r^L \] 这个定理更常用的形式是:唯一可译定长码的最短码长为: \[ L\geq N\frac{\log q}{\log r} \]
定长信源编码定理
引理:设离散无记忆信源的熵为\(H(S)\),用码符号集\(X=(x_1,x_2\cdots x_r)\)对\(S^N\)进行长度为\(L\)的定长编码,\(\forall \epsilon >0,\delta>0\),如果 \[ \frac LN \log r\geq H(s)+\epsilon \] 则\(N\)足够大时,译码错误率小于\(\delta\),反之,如果 \[ \frac LN \log r\leq H(s)-2\epsilon \] 则\(N\)足够大时,译码错误趋向于\(1\).
也就是说,当 \[ L\log r>NH(s) \] 即码长为\(L\)的符号序列能携带的最大信息量大于\(N\)次扩展信源的信息熵时,\(N\)足够大时,就可以近似实现无失真传输。
对于定长编码,定义编码速率: \[ R=\frac{L\log r}{N} \] 编码效率: \[ \eta = \frac {H(s)}{R} \] 由定长信源编码定理知道,最佳编码效率为: \[ \eta = \frac{H(s)}{H(s)+\epsilon} \] 如果允许错误概率\(p_e<\delta\),信源长度\(N\)要满足: \[ N\geq \frac{D[I(s_i)]}{\epsilon^2\delta} \] 其中\(D[I(s_i)]\)是自信息量的方差。代入,有: \[ N\geq \frac{D[I(s_i)]}{H^2(s)}\frac{\eta^2}{(1-\eta)^2\delta} \]
【例】现有离散无记忆信源: \[ \begin{bmatrix} S\\P \end{bmatrix}=\begin{bmatrix} s_1 & s_2\\ \frac 34 & \frac 14 \end{bmatrix} \] 对其采取等长二元编码,编码效率\(\eta = 0.96\),允许错误概率不大于\(10^{-5}\),求\(N\)最少是多少
【解】信源信息熵为 \[ H(s)=\frac 34\log_2 \frac 43+\frac 14+\log_24=0.811 \] 自信息量的方差为: \[ \begin{aligned} D[I(s_i)]&=E[I^2(s_i)]-E^2[I(s_i)]\\ &=\sum_{i=1}^2p_i(\log_2 p_i)^2-[H(s)]^2\\ &=0.4715 \end{aligned} \] 则 \[ N\geq \frac{0.4615}{0.811^2}\frac{0.96^2}{0.04^2\times 10^{-5}}=4.13\times 10^7 \]
变长码
变长码无需很长的码长就能实现高效率的无失真信源编码。关于信源符号数、码字长度之间应该满足什么条件,才能构成唯一可译码,有:
设信源符号集为\(S=(s_1\cdots s_q)\),码符号集为\(X=(x_1\cdots x_r)\),对信源进行编码,对应的码字为\(W=(W_1\cdots W_q)\),每个码的码长为\(l_1\cdots l_q\),则唯一可译即时码存在是充要条件是: \[ \sum_{i=1}^q r^{-l_i}\leq 1 \] 这叫“克拉夫特不等式”。
如果把上面的定理中的“唯一可译即时码”换成“唯一可译码”,其它都不变,定理仍然成立。
变长编码定理
如果传输一个码符号需要\(t\)秒,那么编码后信道每秒传输的信息量为: \[ R_t=\frac{H(s)}{\overline L t} \] 则平均码长越短,\(R_t\)越大,信息传输的速率越快。因此,人们感兴趣的码是平均码长最短的码。
对于固定的信源和码符号集,如果有一种唯一可译码的平均码长小于所有其它唯一可译码,则称其为紧致码。
对于离散无记忆信源\(S\)及其\(N\)次扩展信源\(S^N\),码符号集中有\(r\)个符号,对\(S^N\)进行编码,则总可以找到一种编码方式构成唯一可译码,而且码字平均长度满足: \[ \frac{H(S)}{\log r}+\frac 1N>\frac{\overline L_N}{N}\geq \frac{H(S)}{\log r} \] 当\(N\to \infty\),有: \[ \lim _{N\to \infty}\frac{\overline L_N}{N}=\frac{H(s)}{\log r} \] 以下记: \[ H_r(S)=\frac{H(S)}{\log r} \] 把这个结论推广到平稳遍历的有记忆信源,一般离散信源,马尔可夫信源,有: \[ \lim _{N\to \infty}\frac{\overline L_N}{N}=\frac{H_{\infty}}{\log r} \] 类似的,定义变成编码的编码速率: \[ R=\frac{\overline L_N}{N}\log r \] 编码效率: \[ \eta =\frac{H(S)}{R}=\frac{H_r(S)}{\overline L} \]
变长码的编码方法
香农编码
香农编码的编码方式如下:
把信源发出的\(N\)个符号按概率递减的顺序从上到下排列
按下式计算第\(i\)个消息的二进制代码组的码长\(l_i\),并取整: \[ -\log p(s_i)\leq l_i<-\log p(s_i)+1 \]
计算第\(i\)个消息的累加概率 \[ P_i =\sum_{k=1}^{i-1}p(s_k) \]
把累加概率转换成二进制小数,并截取小数点后的前\(l_i\)位作为第\(i\)个消息的编码。
【例】对以下信源进行香农编码
消息 s1 s2 s3 s4 s5 s6 s7 概率 0.2 0.19 0.18 0.17 0.15 0.1 0.01 【解】香农编码表如下:
消息序号 消息概率 累加概率 \(-\log p(s_i)\) 码组长度 二进制代码 s1 0.2 0 2.3 3 000 s2 0.19 0.2 2.4 3 001 s3 0.18 0.39 2.4 3 011 s4 0.17 0.57 2.5 3 100 s5 0.15 0.74 2.7 3 101 s6 0.1 0.89 3.3 4 1110 s7 0.01 0.99 6.6 7 1111110
霍夫曼编码
霍夫曼编码是一种紧致码,它的编码过程为:
- 把\(q\)个符号按概率分布从大到小的顺序排列
- 用
0,1分别代表概率最小的两个信源,把这两个符号合并成一个新符号,从而得到包含\(q-1\)个符号的缩减信源 - 把缩减信源的符号概率仍从大到小排序
- 重复2~3,直到信源只剩下两个符号为止,把这最后两个符号用
0和1表示,然后从最后一级缩减信源开始向前返回,得到编码。
【例】对以下信源进行霍夫曼编码:
符号 s1 s2 s3 s4 s5 概率 0.4 0.2 0.2 0.1 0.1 【解】
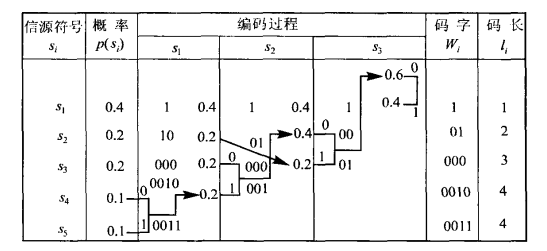
费诺码
费诺码的编码过程如下:
- 把\(q\)个符号按概率分布从大到小的顺序排列
- 把依次排列的信源符号依概率分为两大组,使两个组的概率和尽可能相等,然后给各组赋予一个二进制码符号
0和1 - 把上面这两大组中每一大组的符号再分成两部分,使得划分后两小组的概率和尽可能相等,然后给各组赋予一个二进制码符号
0和1 - 重复2~3,直到每个组都只剩下一个符号为止
【例】对以下信源进行费诺编码
符号 s1 s2 s3 s4 s5 s6 s7 概率 0.2 0.19 0.18 0.17 0.15 0.1 0.01 【解】
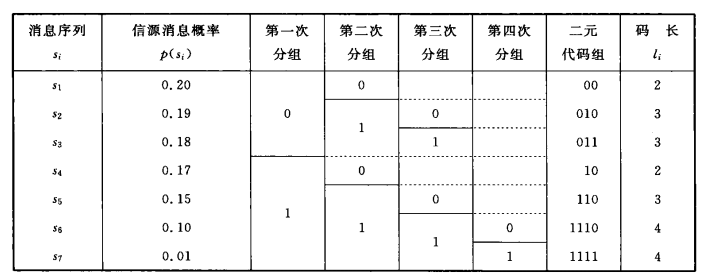
平均码长为 \[ \overline L=2.74 \] 信息速率 \[ R=\frac{H(s)}{\overline{L}}=0.953\quad bit/\text{码元} \]
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
