数字电路·组合与时序之章
组合逻辑电路
设计分析
略,无非是列功能表、真值表、画卡诺图、化简、转换形式、连电路。
经典组合逻辑电路模块
编码器
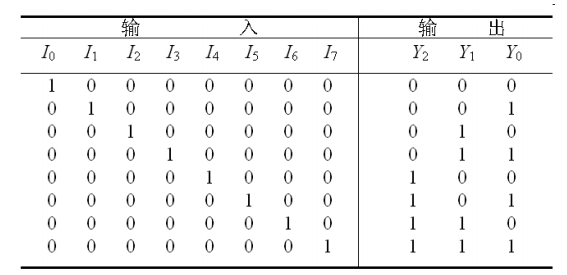
8(位)-3(线)编码器
其基本功能是输入8位中的一位表示被编码的十进制数,3条输出线表示这个十进制数的二进制形式。
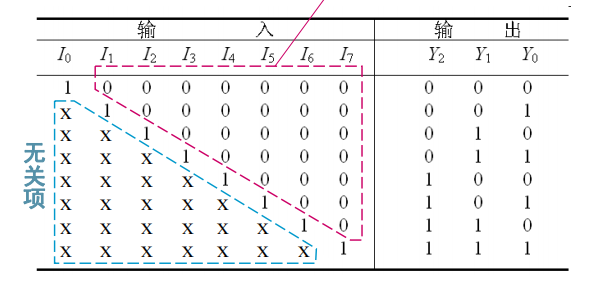
优先编码器
相比于83编码器,优先编码器的输出取决于最高为1的那一位。
74HC148优先编码器
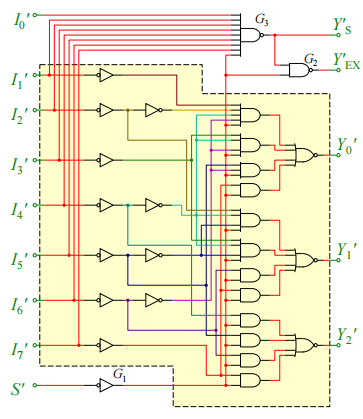
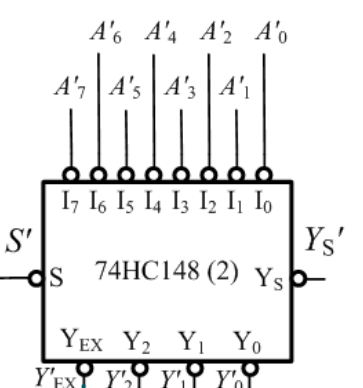
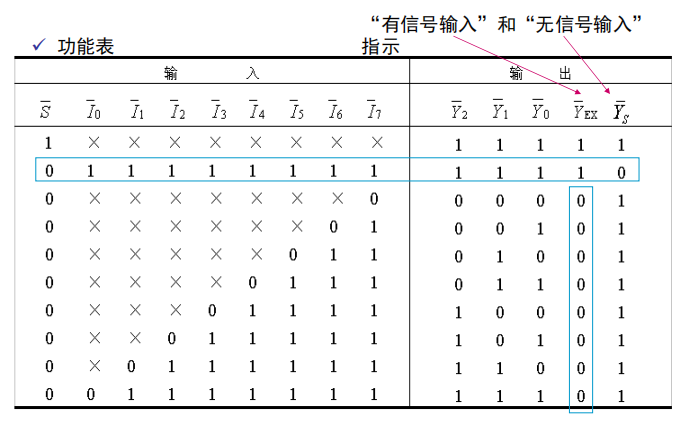
其中的\(A_i,Y_i\)是完成基本功能的输入输出端,此外,它还有一些其它的端口,能进行扩展功能:
- \(\overline S\)选通输入端,当且仅当\(\overline S=0\),电路正常工作,否则,所有输出都被封锁在高电平。
- \(\overline {Y_S}\)选通输出端,当它为0时表示:电路工作但无编码输入
- \(\overline {Y_{EX}}\)扩展输出端,它为0时表示:电路工作且有编码输入
译码器
译码器就是编码器的逆,输入三个信号表示一个二进制数,输出八个信号中的一个表示那个二进制数的十进制表示。
常用的译码器是74138译码器:
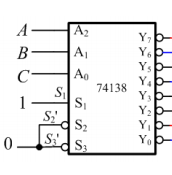
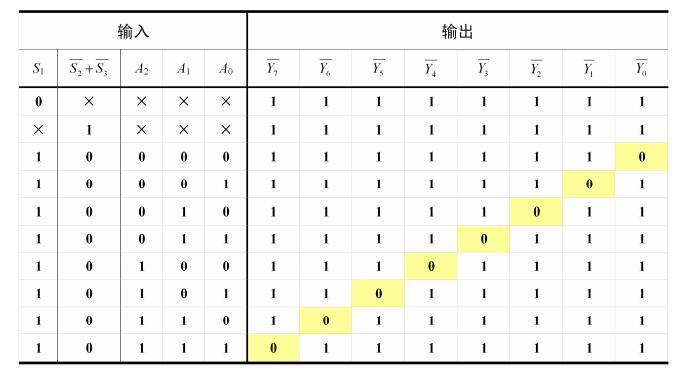
它有三个附加控制器:\(S_1,\overline S_{2},\overline S_3\)。当\(S_1=1,\overline S_{2}=\overline S_3=0\)时,电路正常工作,否则,所有输出端为高电平。
使用多个译码器进行串接时,往往可以在第二个译码器上对高位取反,以此来达到串联效果。
数据选择器
数据选择器有若干个输入信号,一个选择信号(可能有多位)和一个输出。由选择信号决定输出接哪个输入信号。
常用的数据选择器是74HC153双四选一数据选择器。
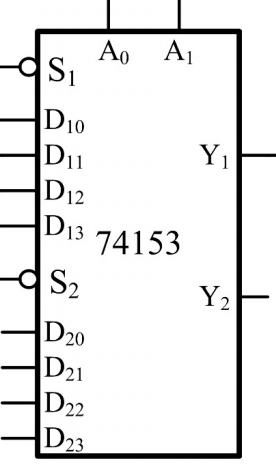
其中\(D\)表示输入信号,\(A_1A_0\)共同表示一个二进制数,是选择信号,\(Y\)是输出信号,\(S\)是选通输入端。有时候我们只用单四选一,这时候把其它管脚留空即可,但是不能把这个片劈成两半。
数值比较器
略,没啥说的,都差不多。
常用的数值比较器是7485数值比较器
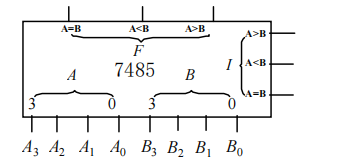
其中\(A,B\)是待比较的数值,\(F\)是输出。而\(I\)则是当数值比较器扩展时,来自低位的比较结果。比如说,要实现八位数值的比较,我们可以这样级联:
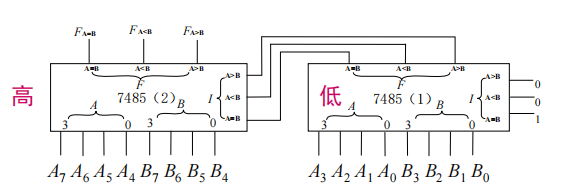
首先比较高四位。如果高四位出现了不同,那么自然可以直接输出。如果高四位相同,那么就需要另接入一个数值比较器来比较下四位,然后把下四位的比较结果通过\(I\)端反馈到高位的比较器,再由负责高位的比较器来输出最终的结果。
也就是说,当\(AB\)不相等时,输出和\(I\)无关,直接输出\(AB\)的关系,否则,直接输出\(I\)。
加法器
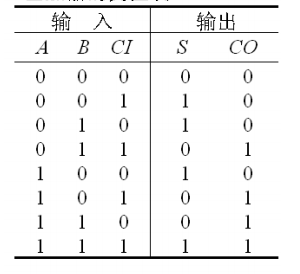
全加器有三个输入\(A,B,CI\),其中\(AB\)表示两个加数,\(CI\)表示上个全加器产生的进位信号。有两个输出:\(S,CO\),\(S\)表示和,\(CO\)表示有无进位。
这个功能很简单就能描述:
1 | |
半导体存储电路
基本的半导体存储电路有锁存器、触发器、寄存器、存储器等。其中触发器可按结构分为基本、同步、主从、边沿触发器,按触发方式分为电平、脉冲、脉冲边沿触发器,按逻辑功能分为RS、JK、D和T触发器等。
SR锁存器
SR锁存器是最基本的半导体存储电路。一般来说,我们所谓的锁存器,都指的是SR锁存器。其电路图如下:
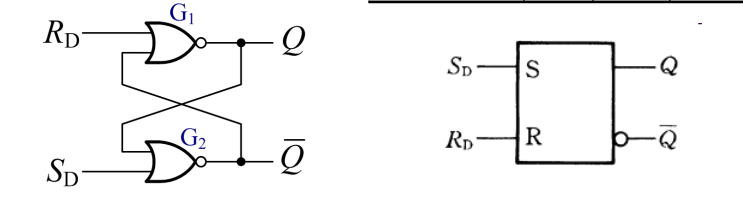
由于或非门可以被“锁定”的特性,这个电路具有了锁存的功能。其状态转移图如下:
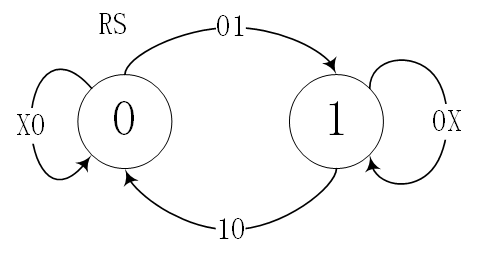
状态方程如下: \[ \left\{\begin{array}{c} Q^{n+1}=S_{\mathrm{D}}+\overline{R_{\mathrm{D}}} \cdot Q^n \\ R_{\mathrm{D}} S_{\mathrm{D}} \equiv 0 \end{array}\right. \] 状态表如下:
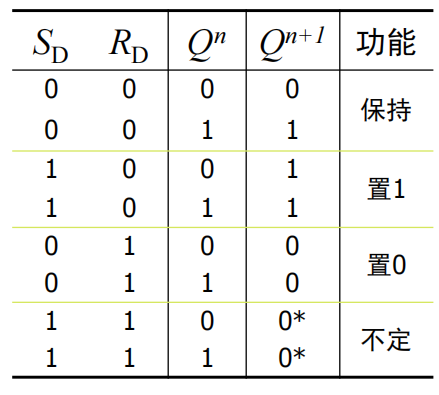
状态转移图、状态方程、状态表,说的都是一件事,那就是这个元件的状态如何变化。在SR触发器中,记住状态表是最高效的分析方法。
在状态表中,我们观察最后两行,这是状态转移图和状态方程中没有考虑到的。这里的“不定”有两种含义。第一种,当电路正常工作时,如果施加\(S_D=1,R_D=1\)的输入,会有\(Q=\overline{Q}=0\)的状态,这既不是定义的“1”状态,也不是定义的“0”状态,所以叫“不定”。第二种是,当电路本来就是上一个状态时,如果同时把\(S,R\)置\(0\),那么电路的输出状态不能确定(这个照着电路图推一推就明白了),于是叫做“不定”。
观察状态转换方法,我们有时将\(S_D\)叫做“直接置位端”,意思是直接把状态置为1;将\(R_D\)叫做“直接复位端”,意思是把状态复位为0,于是这个电路叫做“Ser-Reser Latch”,即“SR锁存器”。
SR锁存器也可以用与非门构造,如下:
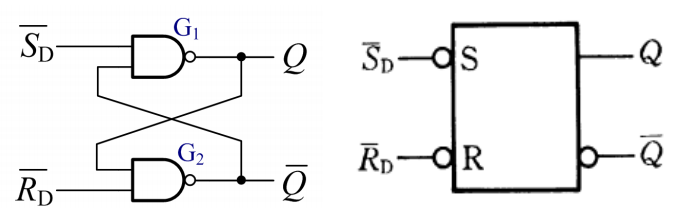
不同的是,这里的\(S_D,R_D\)都变成了低电平有效。
触发器
电平触发
电平触发的意思,就是当且仅当clk信号是有效信号时,触发器的输出状态随着输入信号变化。如果不是有效信号,则保持之前的输出状态。
电平触发有时会因为一些短暂的噪声而影响整个输出,因此我们要考虑其它触发方式
脉冲触发
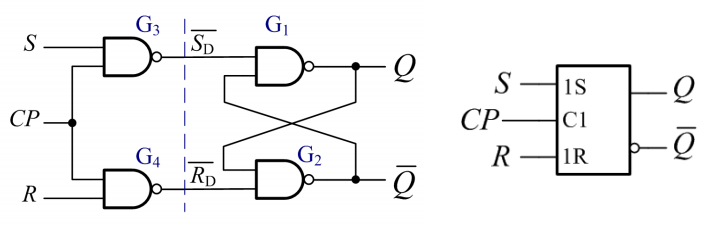
首先来考虑主从SR触发器(也叫“脉冲触发的SR触发器”)。主从SR触发器的结构和符号如下:
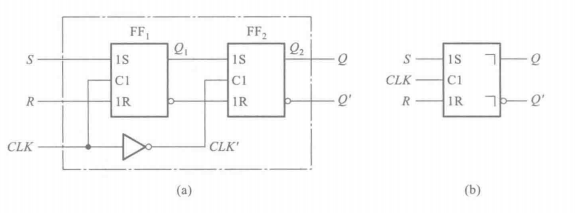
可以看出,一个脉冲触发的SR触发器,是由两个电平触发的SR触发器接成的。\(FF_1\)叫主触发器,\(FF_2\)叫从触发器,主触发器的输出直接接入从触发器的输入。在分析时,应该在高电平先对\(Q_1\)进行分析,之后,再在低电平(注意,从触发器接的时钟信号是翻转的)对\(Q\)进行分析。显然,主触发器在一个高电平时间段内,可以随着输入信号的变化而翻转多次。
接下来我们考虑JK触发器。
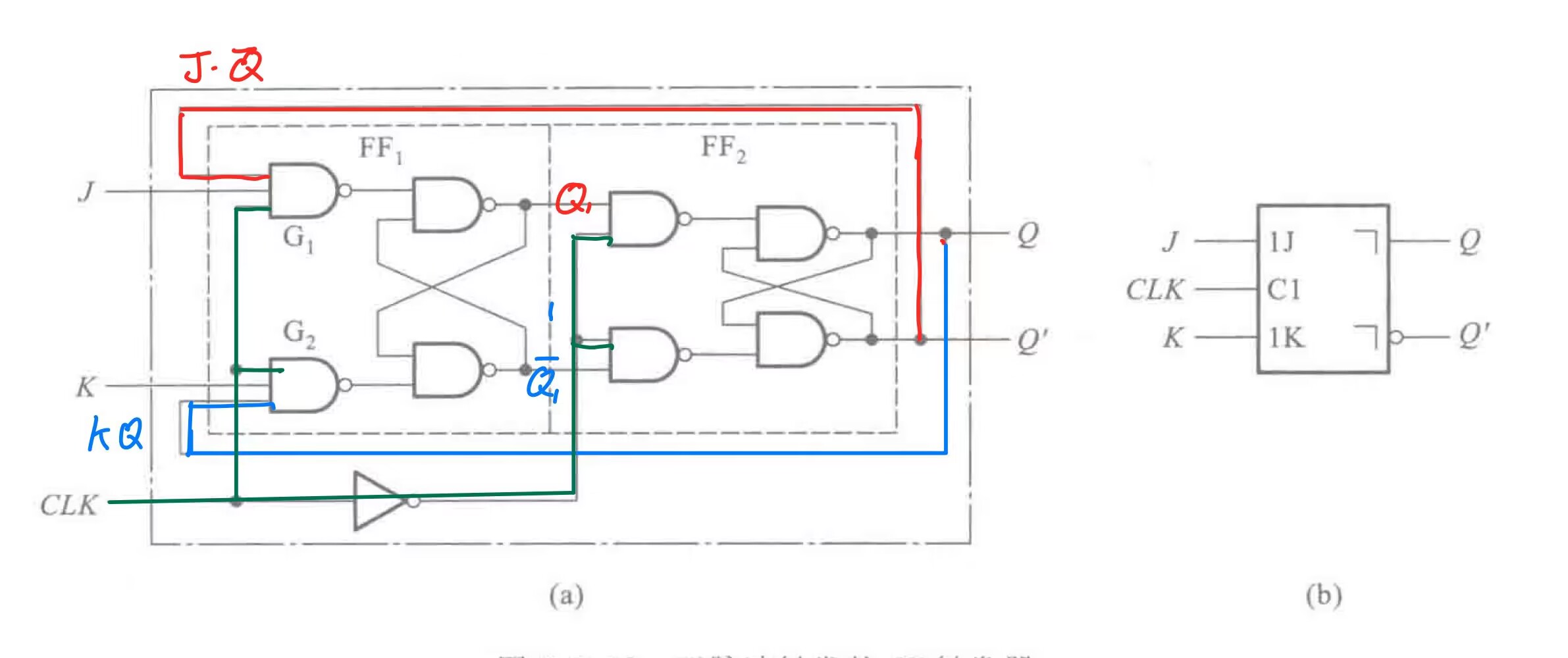
这里在输出端和输入端之间接了一个反馈。即: \[ S=\overline{Q}J,R=QK \] 带入,有: \[ Q^{n+1}=J \cdot \overline{Q^n}+\overline{K} \cdot Q^n \] 这就是JK触发器的状态转移方程,可以写出状态转移图:
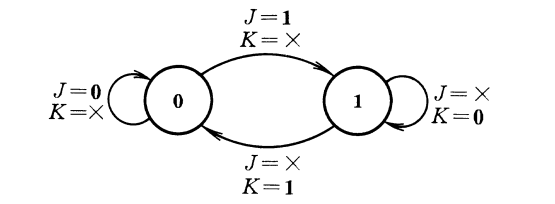
状态表:
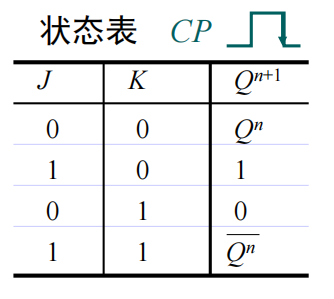
接下来,我们讨论一下JK触发器是怎么进行状态转移的。JK的主触发器仍然是一个电平触发的SR触发器,但是由于JK触发器的反馈机制,当\(Q=0\)时,因为\(R=QK=0\),主触发器只能接受“置1输入信号”;当\(Q=1\)时,因为\(S=\overline QJ=0\),主触发器只能接受“置0(复位)输入信号”,所以这个主触发器在\(CLK=1\)期间至多翻转一次,这就是所谓的“JK触发器的一次性变化现象”。
于是,我们可以知道所谓“脉冲触发”到底是什么意思。
- 触发器的翻转分两步动作,首先,在\(CLK=1\)时,主触发器接收输入信号,进行动作,而从触发器不动。第二步,\(CLK=1\)的信号消失时(有的人把这个动作表述为“下降沿来临时”),从触发器根据主触发器的状态进行动作。由于输出信号是从触发器的输出信号,我们看起来,脉冲触发的触发器进行动作总是发生在\(CLK\)信号的下降沿。
- 主触发器本来是一个电平触发的SR触发器,所以在\(CLK=1\)的全部时间,输入信号都会对主触发器起作用。
边沿触发
边沿触发是最简单的,它的次态仅仅取决与\(CLK\)信号的上升沿或下降沿来临的瞬间,输入信号的状态。在分析时,只用对触发的边沿那几个有限的点进行分析就行了。
按逻辑功能的分类
SR触发器和JK触发器的逻辑功能前面已经讲了。接下来介绍两种其它的触发器:
T触发器
T触发器的功能简单来说是:“0保持,1取反”,即: \[ Q^{n+1}=T\overline{Q}+\overline{T}Q \]
\(T\) \(Q\) \(Q^{n+1}\) 0 0 0 0 1 1 1 0 1 1 1 0 D触发器
D触发器的功能简单来说是:“延迟一位”,即: \[ Q^{n+1}=D \]
\(D\) \(Q\) \(Q^{n+1}\) 0 0 0 0 1 0 1 0 1 1 1 1
存储器
首先明确一个概念:怎么表达一个存储器的大小呢?书上说:“通常写成(字数)x(每个字的位数)”的形式。什么是字?字就是这个存储器输出的东西。存储器每读入一个地址,就会输出一个01串,这个01串就是一个“字”,这个01串的长度就是“每个字的位数”。那么有人说,假设每个字的位数是\(n\),那么字数难道不会自动是\(2^n\)吗?不是这样的。因为我们可以在不同的地址里存相同的字,也可以不在存储器中存储所有字,这是显而易见的。存储器的每个地址中存法一个字,所以所谓的“字数”其实是有效的地址数。
随机存取存储器RAM
可以随时从任何一个指定的地址读出数据,也可以随时将数据写入任何一个指定的存储单元中去,但是掉电后数据会丢失。其基本结构如下:
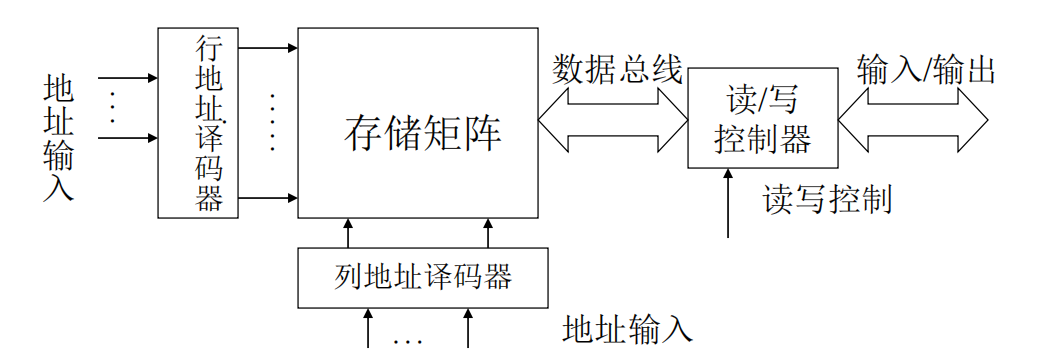
只读存储器ROM
ROM的基本结构如下:
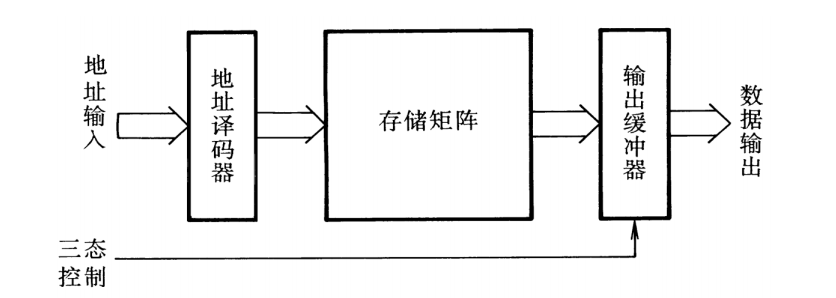
我们可以考察一下二极管ROM的详细结构。
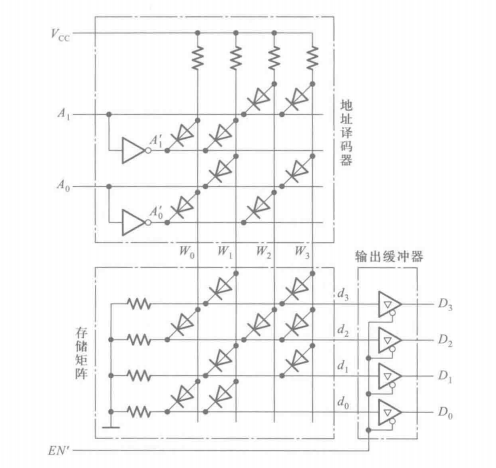
在地址译码器中,看纵列,每个纵列构成了一个二极管与门。于是: \[ \begin{aligned} W_0=\overline{A_0}\ \overline{A_1}\\ W_1=A_0 \overline{A_1}\\ W_2=\overline{A_0}A_1\\ W_3=A_0A_1 \end{aligned} \] 这样一来,就实现了一个译码器,这就是地址译码器。它将输入的二位二进制地址码翻译成\(W_i\)的其中一个信号。
现在看存储矩阵,看横行,每个横行构成了一个二极管或门,比如\(D_3=W_1+W_3,D_2=W_0+W_2+W_3,\cdots\),这样一来,输出端\(D\)就能根据\(W\)的选通而输出对应的信号\(\{D_3D_2D_1D_0\}\)了。这就是二极管ROM的工作原理。根据这个原理,我们也可以使用ROM来实现多输出端逻辑函数,不再赘述了。
存储器容量的扩展
位扩展
当字数够用而每个字的位数不够时,可以使用位扩展。位扩展很简单,只需要把所有地址线、读写控制线、\(CS'\)线(CS‘线就是片选输入端,当\(\overline{CS}=0\)时,这个片才工作)统统拧在一起就行了,如下是把8个1024x1位存储器位扩展为一个1024x8位存储器的过程:
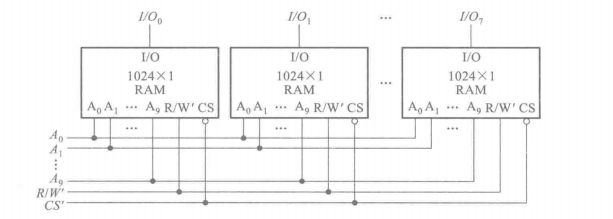
字扩展
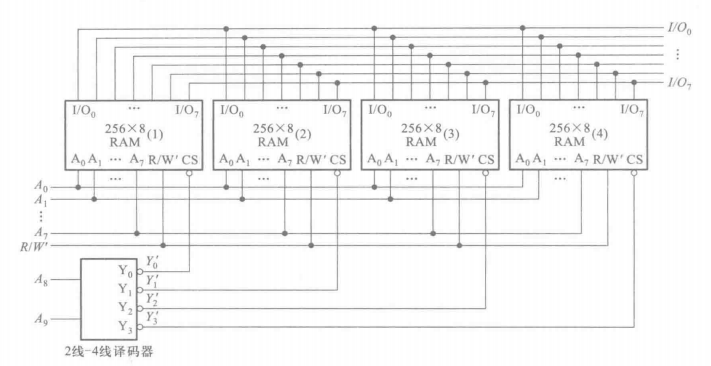
当位数够用而字数不够时,可以使用字扩展。字扩展的接法是:首先把每个片的每个输出端,每个低位地址端,读写控制线并联起来,然后在新的地址位上加入一个译码器,通过译码器和CS端来控制不同的片工作与否,以达到扩展字数的目的。如下图是把4个256x8存储器接成一个1024x8存储器的过程:
时序逻辑电路
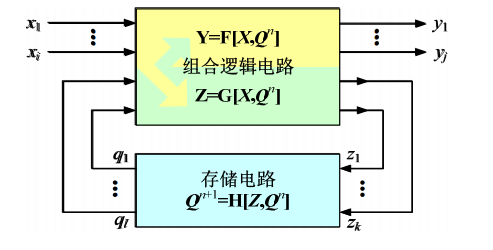
时序逻辑电路的特点是:任意时刻的输出状态不仅仅和当前的输入有关,还和电路之前的状态有关。其基本结构是由存储器电路和组合逻辑电路组成的。如下图所示:
描述时序逻辑,一般用三个方程。下面所说的“Q状态”指的是存储电路中各触发器的输出端状态:
状态方程 \[ Q^{n+1}=H(Z,Q^n) \] 状态方程描述的是前一次的\(Q\)状态和后一次的\(Q\)状态的关系。
驱动方程 \[ Z=Q(X,Q^n) \] 驱动方程描述的是触发器各输入端口和电路的\(Q\)状态以及输入信号的关系。
输出方程 \[ Y=F(X,Q^n) \] 输出方程描述的是电路的输出信号和输入信号以及\(Q\)状态的关系。
时序逻辑电路按照电路状态转换情况不同,分为同步时序逻辑电路(所有触发器共用一个时钟信号)、异步时序逻辑电路(有些触发器的时钟信号可能是其它触发器的输出或者其它信号,总之不是共用一个时钟信号)。
按照输出变量是否和输入变量直接相关,分为Mealy型(外部输出和触发器的状态以及输入信号有关)和Moore型(外部输出仅与触发器的状态有关)。
时序逻辑电路的分析
分析时序逻辑电路的基本纲领是:
- 根据电路逻辑图写出各个触发器的驱动方程(基本形式为:\(\text{触发器输入端信号}=f(Q^n,\text{输入信号})\))和输出方程
- 把各驱动方程带入触发器的特性方程,得到电路的状态方程(基本形式为:\(Q^{n+1}=f(Q^n,\text{输入信号})\))
- 列出逻辑转换表、逻辑转换图
- 分析电路功能
以下以一些例子说明这个过程。
同步时序逻辑电路分析
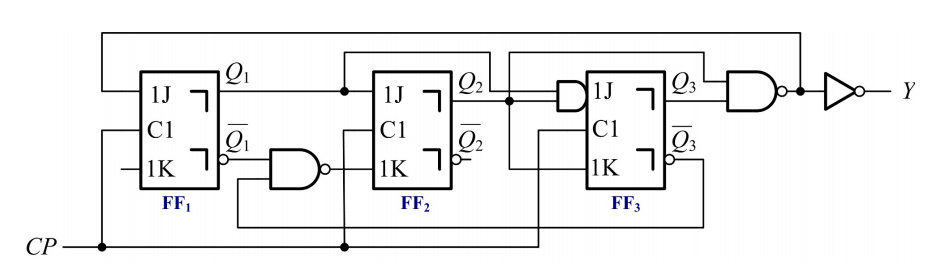
列电路驱动方程: \[ \begin{cases}J_1=\overline{Q_2} \cdot Q_3 & K_1=1 \\ J_2=Q_1 & K_2=\overline{\overline{Q_1} \cdot \overline{Q_3}} \\ J_3=Q_1 \cdot Q_2 & K_3=Q_2\end{cases} \] 输出方程: \[ Y=Q_2Q_3 \]
电路所用触发器是\(JK\)触发器,其特性方程为:\(Q^{n+1}=J\bar Q+\bar KQ\),把驱动方程带入特性方程,有: \[ \begin{aligned} & Q_1^{n+1}=\overline{Q_2} \cdot Q_3 \cdot \overline{Q_1} \\ & Q_2{ }^{n+1}=Q_1 \cdot \overline{Q_2}+\overline{Q_1} \cdot \overline{Q_3} \cdot Q_2 \\ & Q_3{ }^{n+1}=Q_1 \cdot Q_2 \cdot \bar{Q}_3+\overline{Q_2} \cdot Q_3 \end{aligned} \]
列出状态转移表:
这个表有三部分:\(Q,Q^{n+1},Y\)。其中\(Q\)栏要预先穷举所有组合,\(Q^{n+1}\)栏和\(Y\)栏根据状态方程和输出方程书写。
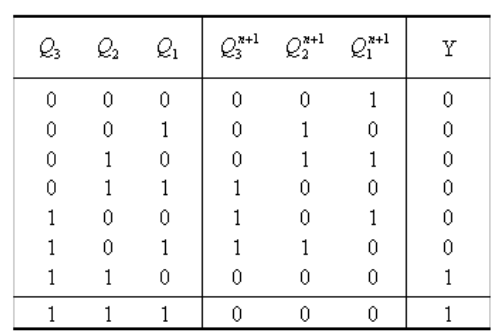
分析,得这个电路是一个七进制加法计数器,\(Y\)是进位信号。
同步Mealy时序逻辑电路分析
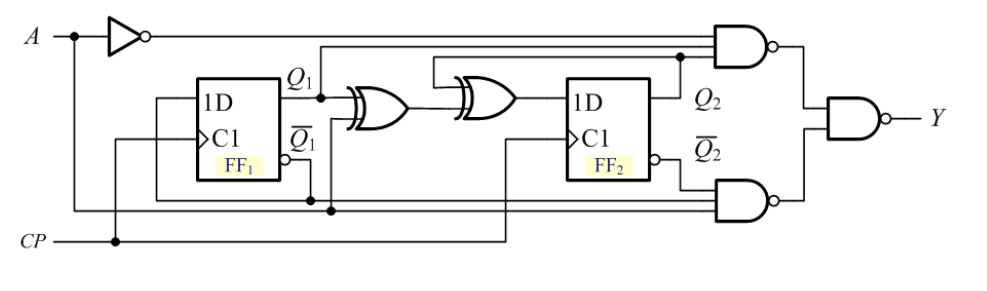
写驱动方程 \[ \begin{aligned} & D_1=\overline{Q_1} \\ & D_2=A \oplus Q_1 \oplus Q_2 \end{aligned} \]
由\(D\)触发器的特性方程\(Q^{n+1}=D\),写状态方程: \[ \begin{aligned} & Q_1^{n+1}=D_1=\bar{Q}_1 \\ & Q_2^{n+1}=D_2=A \oplus Q_1 \oplus Q_2 \end{aligned} \]
写输出方程: \[ Y=\overline{\overline{\bar{A} Q_1 Q_2} \cdot \overline{A \overline{Q_1} \overline{Q_2}}}=\bar{A} Q_1 Q_2+A \overline{Q_1} \overline{Q_2} \]
写状态转移表:
A Q2 Q1 Q2* Q1* Y 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 1 1 1 0 0 经分析,其是四进制加减计数器,输入控制加减。状态转换图如下:
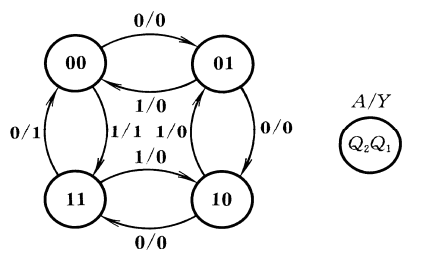
异步时序逻辑电路分析
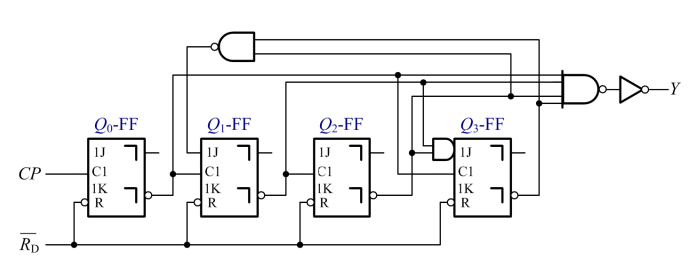
写出驱动方程: \[ \begin{cases} J_0=1 & K_0=1 & cp_0=CP\downarrow\\ J_1=\overline{\overline{Q_2} \cdot \overline{Q_3}} & K_1=1 & cp_1=\bar Q_0\downarrow\\ J_2=1 & K_2=1 & cp_2=\bar Q_1\downarrow\\ J_3=\bar Q_1\bar Q_2 & K_3=1 & cp_3=\bar Q_0\downarrow \end{cases} \]
根据\(JK\)触发器的特性方程\(Q^{n+1}=J\bar Q+\bar KQ\),写出状态方程: \[ \begin{cases} Q_0^{n+1}=\left.\overline{Q_0}\right|_{CP \downarrow}\\ Q_1^{n+1}=Q_2 \overline{Q_1}+Q_3 \left.\overline{Q_1}\right| _{\bar Q_0 \downarrow}\\ Q_2^{n+1}=\left.\overline{Q_2}\right|_{\overline{Q_1} \downarrow}\\ Q_3^{n+1}=\overline{Q_1} \cdot \overline{Q_2} \cdot \left. \overline{Q_3} \right| _{\overline{Q_0} \downarrow} \end{cases} \]
写状态转换表。
首先画一张空表

然后填写Q和已确定的\(cp_0\)
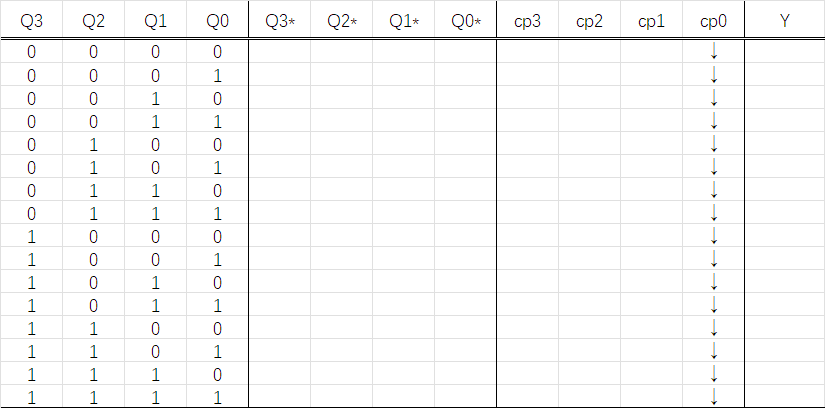
写出可以写出的\(Q^{n+1}\),比如\(Q_0^{n+1}\)
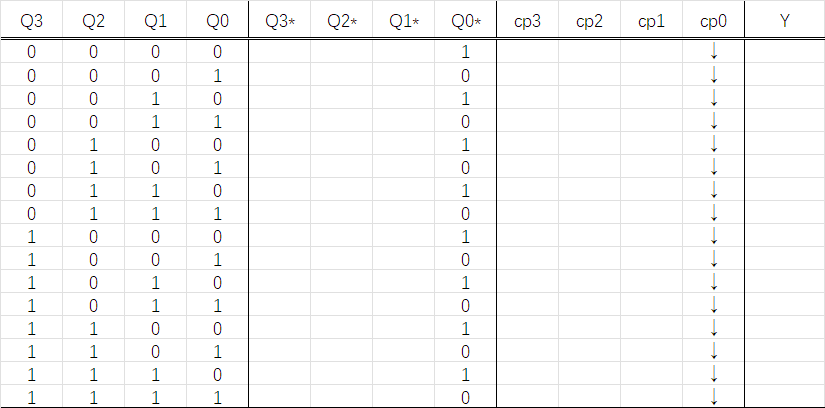
根据Q0*,写出由Q0*确定的时钟信号\(cp_1\),\(cp_3\).因为这两个信号都是\(\bar Q_0\downarrow\),所以在\(Q_0^{n+1}=1\)的地方画下箭头
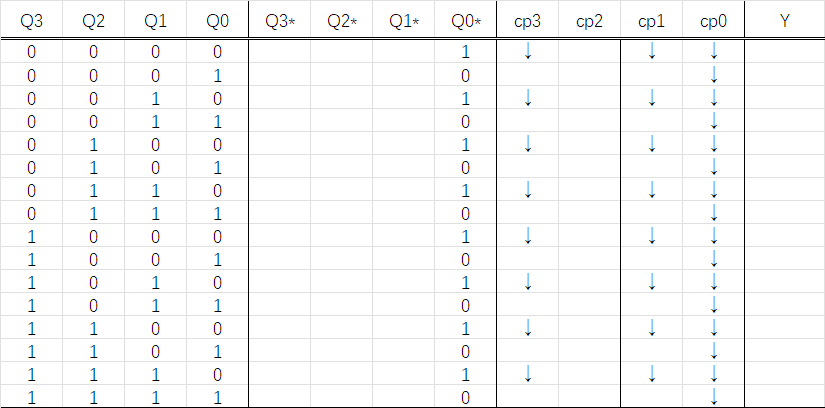
根据已经确定的\(Q,cp_1,cp_3\),填写\(Q_1^{n+1},Q_3^{n+1}\).在\(cp\)有下降沿时,根据状态方程计算状态;当\(cp\)不是下降沿时,直接保持\(Q_1^n,Q_3^n\)(原状态)的值
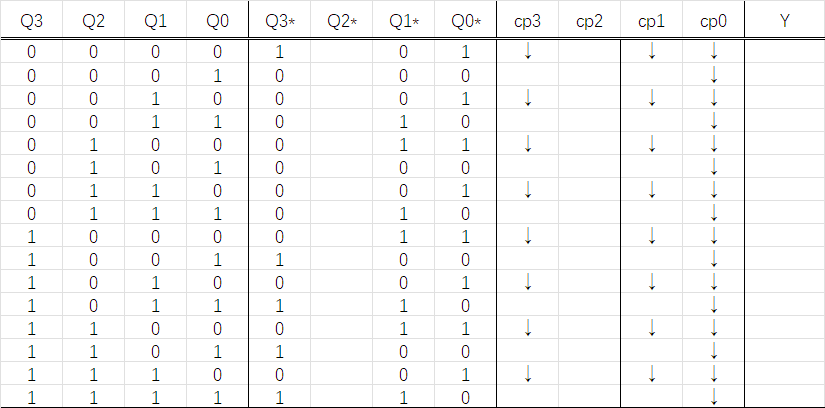
根据\(Q_1^{n+1}\),写出\(cp_2\)(连续1串的末尾处填写↓),仿照上面的过程填写\(Q_2^{n+1}\),最后填写\(Y\).
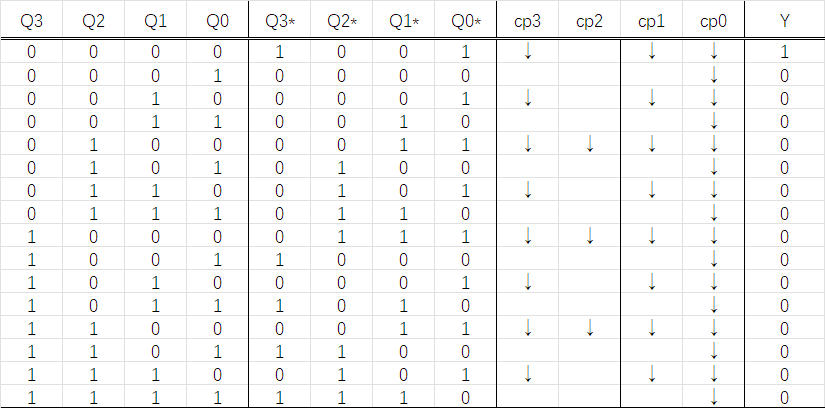
根据表格画出状态转移图,发现其为模十减法计数器
时序逻辑电路设计
设计时序逻辑电路的纲领就是把分析的过程反过来
- 根据设计要求设定状态,绘制状态转换图和表
- 根据触发器类型对状态方程进行逻辑化简
- 写出输出方程和驱动方程
- 根据输出方程和驱动方程画电路图
- 验证自启动性
下面以一些例子说明这个过程:
同步时序逻辑电路设计
【例】设计一个同步13进制加法计数器。
绘制状态转换图:
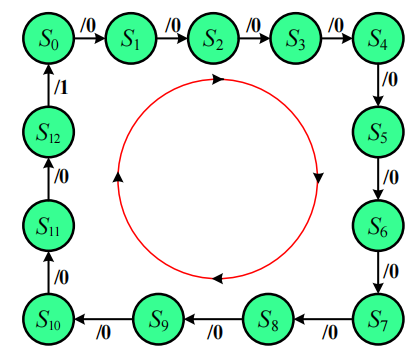
根据图列出状态转换表:
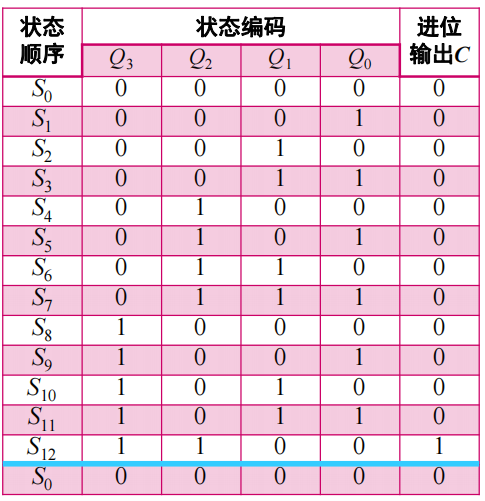
进行逻辑化简,画卡诺图:
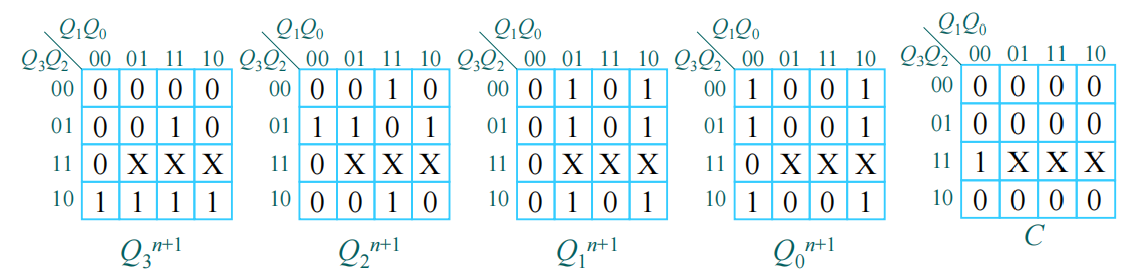
在使用JK触发器时,因为JK触发器的特性方程是(以\(Q_3\)为例子): \[ Q_3^{n+1}=J\cdot \overline{Q_3^n}+\overline{K}\cdot Q_3^n \] 所以我们终究是要化简成像这样的形式,才能进行下一步驱动方程的书写的。所以,在化简时,我们可以在卡诺图中画一条“鸿沟”,把\(Q_3\)和\(\overline{Q_3}\)的部分分割开,合并“1”格画卡诺圈时不跨越“鸿沟”,这样的话,化简出来就直接是上面式子的形式了。
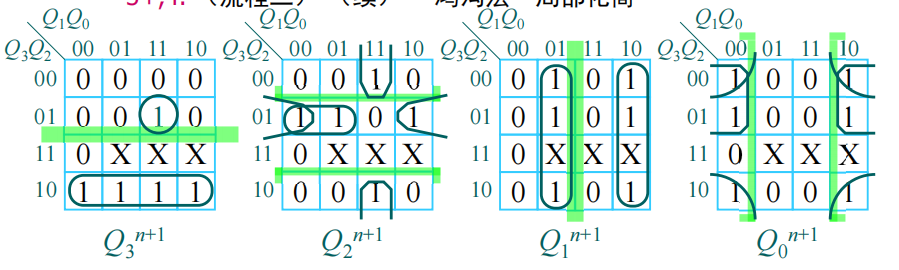
如图,可以写出各状态方程: \[ \begin{cases} Q_3^{n+1}=Q_2Q_1Q_0\cdot \overline{Q_3}+\overline{Q_2}\cdot Q_3\\ Q_2^{n+1}=Q_1Q_0\cdot \overline{Q_2}+(\overline{Q_3}\ \overline{Q_1}\cdot Q_2+\overline{Q_3}\ \overline{Q_0}\cdot Q_2)\\ Q_1^{n+1}=Q_0 \cdot \overline{Q_1}+\overline{Q_0} \cdot Q_1\\ Q_0^{n+1}=(\overline{Q_3} \cdot \overline{Q_0}+\overline{Q_2} \cdot \overline{Q_0}) \end{cases} \]
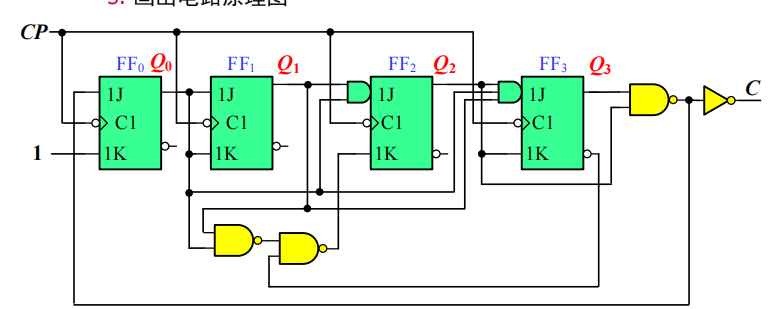
根据JK触发器的特性方程,可以直接写出驱动方程: \[ \begin{cases} J_3=Q_2Q_1Q_0 & K_3=\overline{\overline{Q_2}}=Q_2\\ J_2=Q_1Q_0 & K_2=\overline{\overline{Q_3}(\overline{Q_1}+\overline{Q_0})}=Q_3+(Q_1Q_0)\\ J_1=Q_0 & K_1=Q_0\\ J_0=\overline{Q_2}+\overline{Q_3} & K_0=1 \end{cases} \]
画出电路图
异步时序逻辑电路设计
【例】用JK触发器设计一个异步五进制计数器
绘制状态转换图(略),时序波形图:
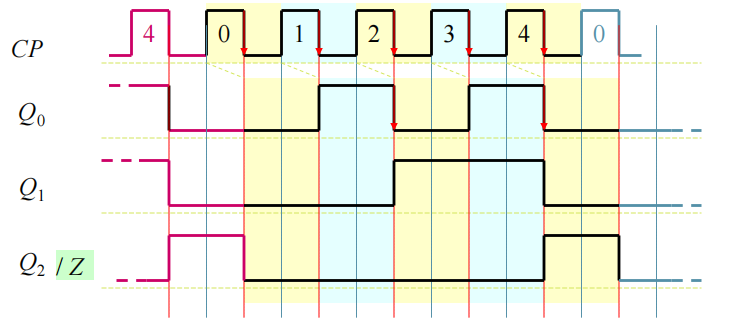
在保证状态变化的时候必有触发脉冲的前提条件下, 选择在状态不变的时候触发脉冲最少的, 使得 \(\mathrm{JK}\) 的输入条件简化。根据以上准则,选定各触发器的触发信号源;列写状态转移表:
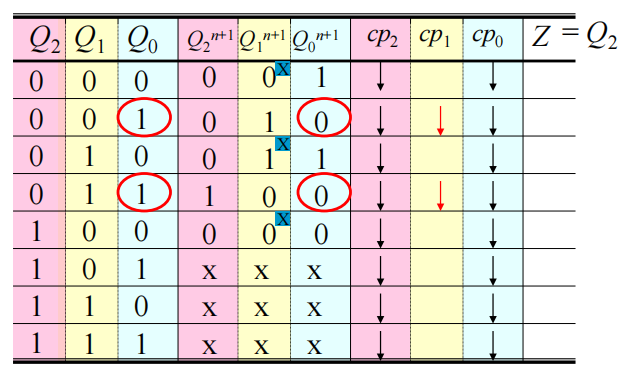
把状态转换表变成卡诺图形式,逻辑化简,写出逻辑表达式
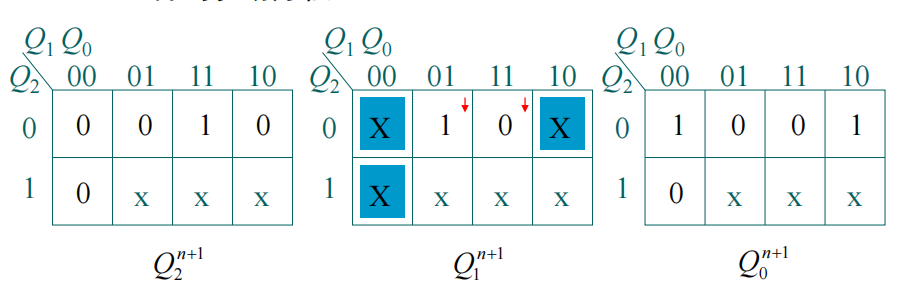
状态方程: \[ \begin{cases} Q_2^{n+1}=Q_1Q_0\cdot\overline{Q_2}\\ Q_1^{n+1}=\overline{Q_1}\\ Q_0^{n+1}=\overline{Q_2}\cdot\overline{Q_0} \end{cases} \] 驱动方程: \[ \begin{cases} J_2=Q_1Q_0 & K_2=1\\ J_1=1 & K_1=1\\ J_0=\overline{Q_2} & K_0=1 \end{cases} \]
计数器
计数器是用以统计输入脉冲CP个数的电路。常用的计数器有以下这么几种:
74161:4位二进制同步加法计数器
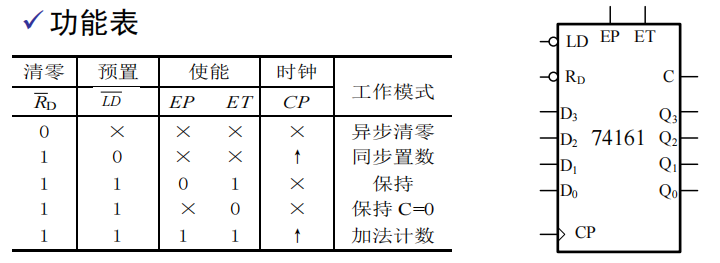
74191:四位二进制同步可逆计数器
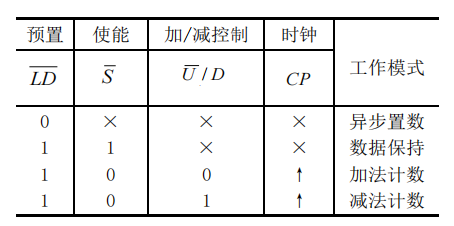
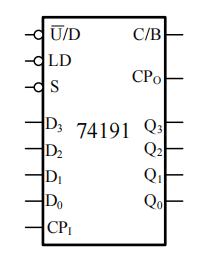
74160:十进制同步加法计数器
其逻辑符号和功能表和74161相同,仅靠上面的数字区分。
任意进制计数器的构成
假设已经有了\(N\)进制计数器,要求通过链接、外加电路的方法得到\(M\)进制计数器。
\(M<N\)时
主要方法有置零法和置数法两种。置零法是在电路从\(S_0\)计数到\(S_M\)时,外接一个\(M\)的译码器,产生一个置零信号,接入置零端。因为电路一经过\(S_M\)状态就会产生置零信号,进而被置入\(S_0\)状态,因此\(S_M\)并不会出现在稳定循环中。以上是异步置零的情况,如果是同步置零的话,需要在\(S_{M-1}\)处进行译码,传回置零信号,然后在下一个时钟触发置零。其逻辑转换图如下:
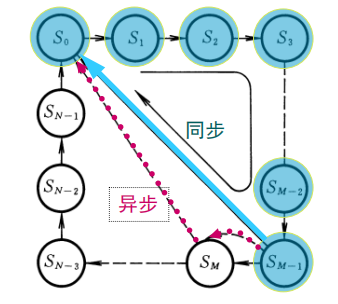
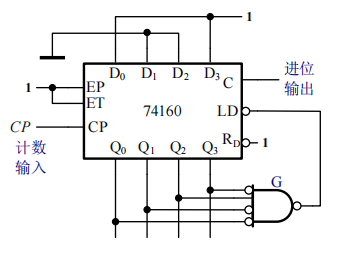
下图是用置零法把同步十进制计数器74160接成同步六进制计数器的电路图:
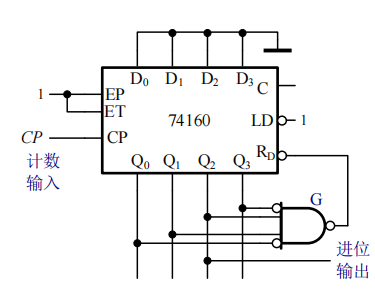
这里的清零端是异步清零。此时标志“进位”这个动作发生的信号是进位输出信号的下降沿。这种接法的清零信号持续时间非常的短,有可能导致电路出错。可以在进位输出前加一个锁存器,如下:
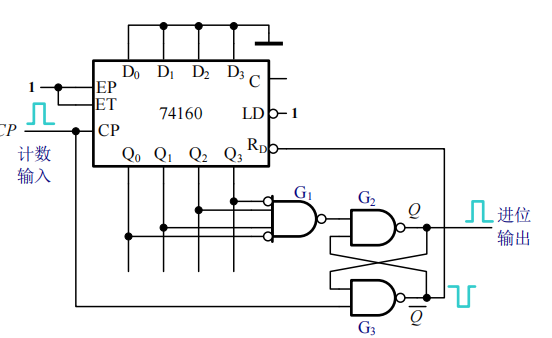
此时如果电路进入\(S_6(0110)\)状态,在\(G_1\)门后输出低电平,把与非门SR锁存器置1,\(\bar Q\)端输出低电平,接入低电平有效置零端\(R_D\),把电路置零。而因为锁存器的存在,置零信号会维持一段时间,直到计数脉冲回到低电平,SR锁存器才被置零。
置位法是通过给计数器重复置入某个数值的方法跳过\(N-M\)个状态,从而获得\(M\)进制计数器的。其逻辑转换图如下:
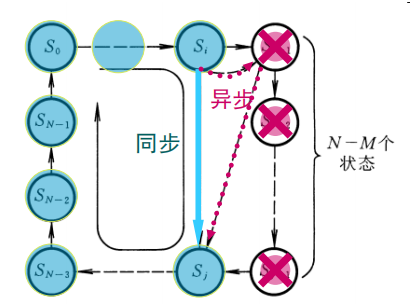
下图是一种用置数法构成的电路:
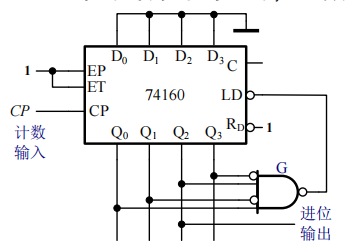
\(M>N\)时
应用多片N进制计数器进行组合。如果M可以因式分解成多个小于N的数之和,即:\(M=N_1N_2\cdots N_n\),那么可以把第\(i\)片计数器接成\(N_i\)进制,然后采用串行进位或者并行进位把他们链接起来。
串行进位指的是以低位片的进位输出信号作为高位片的时钟信号,如下图是把两个十进制计数器用串行接法接成一个一百进制计数器:
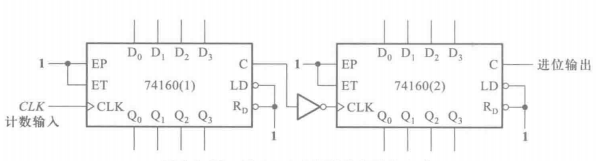
在第9个\(CLK\)信号来临时,第一个计数器的状态为\(1001\),进位输出\(C\)出现高电平,第二片的时钟信号在低电平;当第10个\(CLK\)信号到来时,第一个计数器的状态变为\(0000\),进位输出\(C\)输出低电平,第二片的时钟信号出现一个上升沿,第二片的状态变成\(0001\),以此实现进位功能。
并行进位指的是以低位片的进位输出信号作为高位片的使能信号,两片的时钟同时接\(CLK\)输入信号,如下图是把两个十进制计数器用并行接法接成一个一百进制计数器:
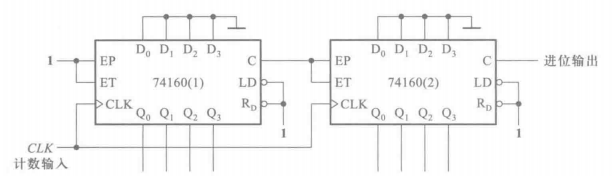
在第9个\(CLK\)信号来临时,第一个计数器的状态为\(1001\),进位输出\(C\)出现高电平,第二片使能开启,开始工作;下个\(CLK\)信号来临,第二片正在工作,状态变为\(0001\),第一片的状态变为\(0000\),进位输出低电平,第二片使能关闭。
如果M是素数,或者不能像这样因式分解,则必须采用整体置零/置数法。
移位寄存器型计数器
环形计数器
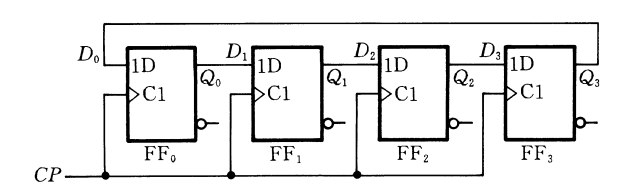
有效循环为\(1000\to 0100\to0010\to0001\to 1000\),不能自启动
扭环形计数器
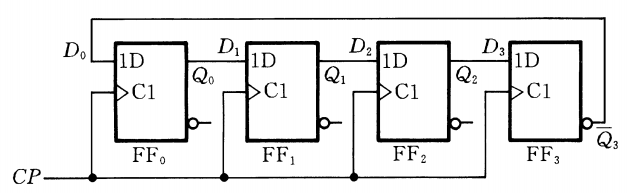
其状态转移图如下:
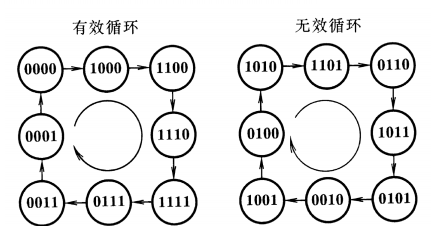
用\(n\)位移位寄存器构成 环形计数器 可以得到\(n\)个状态的有效循环;
用\(n\)位移位寄存器构成 扭环形计数器 可以得到\(2n\)个状态的有效循环。
序列信号发生器
计数译码型
其原理是由一个计数器和一个数据选择器连接,计数器的计数输出连在数据选择器的地址输入上。在数据选择器的信号输入端,预置已知的序列,然后用\(CLK\)驱动计数器,数据选择器根据计数器的状态选择要输出的信号。
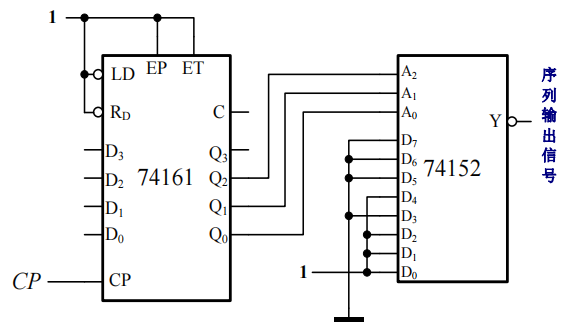
如上图,发生的序列是\(00010111\)。
当然,上面的数据选择器也可以换成自己搭建的组合逻辑译码电路(输入计数信号,输出该信号对应的序列的值)
反馈移位型
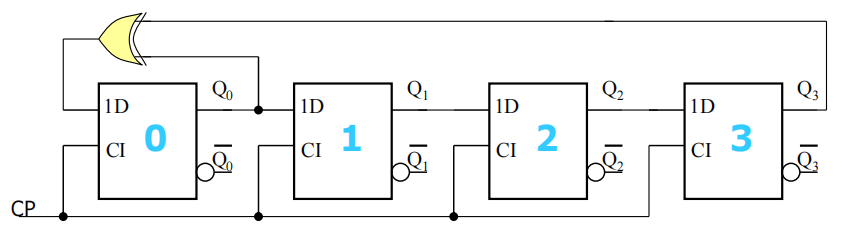
其一般电路如下:
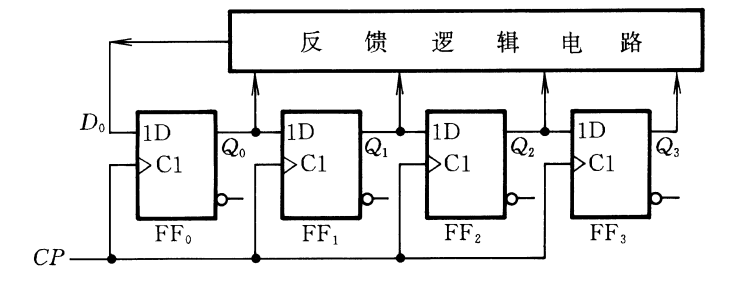
驱动方程为: \[ \begin{aligned} D_0&=F(Q_0,Q_1,\cdots,Q_n)\\ D_1&=Q_0\\ \cdots\\ D_n&=Q_{n-1} \end{aligned} \] 在分析时,完全可以当成一般的同步时序逻辑电路分析,当然也可以用序列发生器的特点简化分析。在分析时,这两者的复杂度区别并不大。
在设计时,首先需要注意,在一个周期内状态编码不能重复;然后根据序列长度\(n\)使用\(\log _2 n\)个\(D\)触发器。接下来以一个例子说明设计过程:
【例】设计反馈移位型序列发生器,序列为\(\{1111\ 0101\ 1001\ 000\}\)(右侧的先出现)。
检查是否有重复和确定触发器数目:
应用四个触发器
确定输出信号的位置
一般来说,选取最后一个触发器的输出端,即\(Q_3\)
设计组合逻辑反馈电路
这里,实际上就是要求写出\(D_0\)和\(Q_3,Q_2,Q_1,Q_0\)的函数关系式。
首先列出表,在\(Q_3\)里填入要输出的序列:
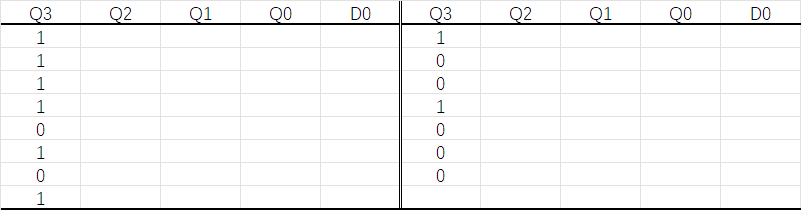
然后因为“移位”的特点,把\(Q_3\)整体向上提一格,填入\(Q_2\);把\(Q_2\)整体往上提一格,填入\(Q_1\);......把\(Q_0\)整体往上提一格填入\(D_0\)(这里的“往上提”是含有循环意味的):

于是,我们就得到了逻辑关系表,然后画卡诺图化简,连电路就行了。
最终结果 \[ D_0=Q_0 \overline{Q_3}+\overline{Q_0} Q_3=Q_0\bigoplus Q_3 \]
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
