实变泛函笔记·泛函分析之章
度量空间和赋范线性空间
度量(距离)空间
如果\(X\)是一个非空集合,对于\(X\)中的任何两个元素\((x,y)\),都有一个实数\(d(x,y)\)与之对应,且满足:
- \(d(x,y)\geq 0\),等号仅在\(x=y\)时取得
- \(d(x,y)=d(y,x)\)
- \(d(x,z)\leq d(x,y)+d(y,z)\),也就是“三角形两边之和大于第三边”
那么称函数\(d\)是\(X\)上的一个距离(度量),\((X,d)\)是距离空间。
事实上,对于任何非空集合,我们都可以让他变成距离空间,大不了定义d(x,y)=(x==y)?0:1嘛。
常用的距离空间
\(R\),\(d(x,y)=|y-x|\)
\(R^n\),有很多种\(d\)的定义,列举三种: \[ \begin{aligned} & d_1(x, y)=\sum_{i=1}^n\left|x_i-y_i\right| \\ & d_2(x, y)=\left(\sum_{i=1}^n\left|x_i-y_i\right|^2\right)^{1 / 2} \\ & d_3(x, y)=\max _{\forall i}\left|x_i-y_i\right|^2 \end{aligned} \]
\(C[a,b]\),指\([a,b]\)上的连续函数构成的集合 \[ d(x, y)=\max _{a \leq t \leq b}|x(t)-y(t)|, \forall x, y \in C[a, b] \] 距离定义为定义域内两个函数垂直距离的最大值
所有序列构成的集合\(S\)
如果\(x=\{\xi_i\},y=\{\eta_i\}\),则 \[ d(x, y)=\sum_{i=1}^{\infty} \frac{1}{2^i} \frac{\left|\xi_i-\eta_i\right|}{1+\left|\xi_i-\eta_i\right|} \] 提示:验证第三条公理只需考察函数\(f(x)=\frac{x}{1+x}\)的单调性
有界序列空间\(l^\infty\) \[ d(x, y)=\sup _{\forall i}\left|\xi_i-\eta_i\right| \]
收敛序列空间\(c\)
距离的定义同有界数列空间一样
\(p\)次可和序列空间\(l^p\) \[ l^p=\left\{x=\left\{\xi_i\right\}\left|\sum_{i=1}^{\infty}\left| \xi_i\right|^p<\infty\right.\right\}, 1 \leq p<\infty \] 距离: \[ d(x, y)=\left(\sum_{i=1}^{\infty}\left|\xi_i-\eta_i\right|^p\right)^{\frac{1}{p}} \]
本质有界可测函数空间\(L^\infty[a,b]\)
本质有界:指除了一个零测集\(E\)以外都有界
距离: \[ d(x,y)=\inf _{m(E)=0}\left\{\sup _{t \in[a, b] \backslash E}|x(t)-y(t)|\right\} \] 意思是:先遍历零测集\(E\),再对每个\(E\)沿着\(x\)轴找到两个函数垂直距离最大的点,再找这个最小的“最大的垂直距离”。
\(p\)次可积函数空间\(L^p\) \[ d(x, y)=\left(\int_a^b|x(t)-y(t)|^p \mathrm{~d} t\right)^{1 / p} \]
距离空间中的拓扑
既然我们定义了距离,那么什么都好办了,距离空间中的拓扑可以对照\(R^n\)中的拓扑的相关定义,包括开球、邻域、内点外点边界点、聚点、开集导集闭包等等。这些定义都是相同的。
【连续映射】设\((X,d),(Y,p)\)都是距离空间,\(T:X\to Y\),如果对于给定的\(x_0\in X,\forall \epsilon >0,\exists\delta>0,s.t. x\in X,d(x,x_0)<\delta,p(T_x,T_{x_0})<\epsilon\),也就是说,如果\(X\)中的两点足够近,那么其映射的像在\(Y\)中也足够近,那么称映射\(T\)在点\(x_0\)处连续。如果\(T\)在\(X\)的每一点都连续,称\(T\)是\(X\)上的连续映射。
连续有两个充要条件,可以辅助判别:
- \(\forall x_0\in X\)当\(X\)中的点列\(x_n\to x_0\)(距离意义上),相应\(Y\)中的像点列\(Tx_n\to Tx_0\)(海涅定理)
- 对\(Y\)中的任何开集\(O\),\(T^{-1}O\)是\(X\)中的开集
【稠密性】设\((X,d)\)是距离空间,\(A\subset X\),对\(\forall x\in X,x\)的任何球中后含有\(A\)中的点,称\(A\)在\(X\)中稠密
【可分性】设\((X,d)\)是距离空间,如果\(X\)中存在可数的稠密子集,那么称\(X\)是可分的。
例如:\(R^n,l^p,s,C[a,b],P[a,b],L^p[a,b]\)都是可分的。
但是\(l^\infty\)是不可分的。
完备距离空间
满足“所有基本列(柯西列)都收敛”[1]的距离空间叫做完备距离空间。
反例1:对距离空间\((Q,d(x,y)=|x-y|)\),有基本列\(x_n=(1+1/n)^n\),在\(Q\)上不收敛。
反例2:对距离空间\((X=(0,1),d(x,y)=|x-y|)\),有基本列\(x_n=1/(n+1)\),在\((0,1)\)上不收敛
典型的完备距离空间有:\(R^n,L^P,l^p,C[a,b]\)
【等距映射】设\((X,d),(\hat X,\rho)\)都是距离空间,如果存在一个映射\(T:X\to \hat X\),使得 \[ d(x,y)=\rho (Tx,Ty) \] 称\(T\)是等距映射。\(X,\hat X\)称为等距同构空间。
【完备化】 对距离空间\((X,d)\),如果有完备距离空间\((\hat X,\rho)\),使得这两个空间等距同构,那么称\(\hat X\)是\(X\)的完备化空间。每个距离空间都有自己的完备化空间。
线性空间
在数域\(K\),集合\(X\)上定义加法、数乘,满足前文提到的“线性运算加法和数乘8条性质”的集合\(X\)称作向量空间或线性空间。
线性空间的性质,我们在线性代数中已经学了很多,这里仅仅列举
- 零向量唯一
- 一个向量的负向量唯一
- 线性子空间的定义(X的子集对加法和数乘封闭)
- 线性组合
- 生成子空间
- 线性无关
- 维数
- 线性子空间的直和\(X=M\bigoplus N=\{m+n|\forall m\in M,\forall n\in N,M\cap N=\emptyset\}\),有\(\dim X=\dim M+\dim N\)
- 补子空间:\(X=M\bigoplus N\),称\(N\)是\(X\)的补。对于一个线性空间\(X\)和它的一个子空间\(M\),\(M\)的补一定存在。
赋范线性空间
设\(X\)是线性空间,且\(\forall x\in X\),存在一个非负实数\(||x||\),且
- \(\|x\| \geq \mathbf{0},\|x\|=0 \Leftrightarrow x=\theta\)
- \(\|\alpha x\|=|\alpha| \cdot\|x\|, \forall \alpha \in C\) (或 \(R)\)
- \(\|x+y\| \leq\|x\|+\|y\|, \forall x, y \in X \quad\) (三角不等式)
那么称\(||x||\)是\(x\)的范数,\((X,||\cdot||)\)为赋范线性空间。
例如:在\(R^n\)空间中的常用范数:
p-范数: \[ \|x\|_p=\left(\sum_{i=1}^n\left|x_i\right|^p\right)^{1 / p} \]
无穷范数: \[ ||x||_\infty=\max |x_i| \]
1-范数: \[ ||x||_1=\sum_{i=1}^n |x_i| \]
任何赋范线性空间都能诱导出一种距离: \[ d(x,y)=||x-y|| \] 但距离空间不一定能诱导出一种范数。
【依范数收敛】 \[ \lim_{n\to \infty}||x_n-x_0||=0 \] 【范数的等价】对于不同的范数,如果存在\(C_1,C_2>0\),使得 \[ C_1||x||_2<||x||_1<C_2||x||_2 \] 那么称这两个范数等价
【巴拿赫空间】如果一个赋范线性空间按照它的范数诱导出来的距离构成的距离空间是完备距离空间,那么称这个赋范线性空间为巴拿赫空间。
【有限维赋范线性空间】有如下性质:
- 维数相等的赋范线性空间都同构
- 有限维线性赋范线性空间必完备且可分
- 赋范线性空间\(X\)是列紧的,和它是有限维等价
- 在其上定义的各种范数都等价
- 从有限维到有限维的线性算子都有界
有界线性算子和连续线性泛函
在泛函分析中,把具有一定性质的元素的集合称为空间,把空间到空间的映射称为算子。算子的概念可以类比于平常所说的映射,也有值域、单、满、双、逆的概念。
【线性算子】如果\(T:(X,||\cdot||_1)\to (Y,||\cdot||_2)\),有: \[ T(\alpha_1x_1+\alpha_2x_2)=\alpha_1Tx_1+\alpha_2Tx_2 \] 则称这个算子\(T\)是线性算子。
【连续算子】 如果\(T:(X,||\cdot||_1)\to (Y,||\cdot||_2)\),有: \[ \text{当}||x-x_0||_1\to 0\text{有}||Tx-Tx_0||_2\to 0 \] 称\(T\)在\(x_0\)处连续。如果\(T\)在\(X\)的每个点都连续,称其为连续算子。
【同构同胚】 如果\(T:(X,||\cdot||_1)\to (Y,||\cdot||_2)\),线性
- 如果\(T\)是双射,那么称\(T\)是线性同构的
- 进一步,如果\(T\)和它的逆都是连续的,那么称\(T\)是线性同胚的
【有界】如果\(T:(X,||\cdot||_1)\to (Y,||\cdot||_2)\),存在常数\(C\),使得对任意\(x\) \[ ||T_x||_2\leq C||x||_1 \] 则称 \(T\)是有界的。有界当且仅当其把任意有界集映射为有界集。
【算子的范数】如果\(T:(X,||\cdot||_1)\to (Y,||\cdot||_2)\)的线性有界算子,称 \[ ||T||=\sup_{\forall x\neq \theta}\frac{||Tx||_2}{||x||_1} \] 为算子\(T\)的范数。
如果在上述“算子”的描述中,\(Y\)是数集,那么这个算子也可以叫做“泛函”。
有界线性算子空间和共轭空间
有界线性算子空间
设全体\(T:X\to Y\)构成一个集合,记作\(\mathcal L(X,Y)\)。则它按范数是赋范线性空间。其中 \[ (A+B)x=Ax+Bx,(\alpha A)x=\alpha(Ax) \] 如果\(X\)是赋范线性空间,\(Y\)是巴拿赫空间(按照它的范数诱导出来的距离构成的距离空间是完备距离空间的赋范线性空间),那么\(\mathcal L(X,Y)\)也是巴拿赫空间。
如果\(A,B\in \mathcal L(X,Y)\),则\(AB\in L(X,Y)\),且\(||AB||\leq ||A||\cdot||B||\)。进一步,有:\(||A^n||\leq ||A||^n\)
【范数的强弱】 对于同一个集合上的两个范数,如果: \[ (||x_n||_1\to 0)\to (||x_n||_2\to 0) \] 称范数1比范数2更强。
算子的逆
设 \(X, Y\) 都是线性赋范空间, \(A: X \rightarrow Y\) 是线性映射. 那么 \(A\) 是单射, 且定义在 \(R(A)\) 上的算子 \(A^{-1}\) 是连续的 \(\Leftrightarrow\) 存在常数 \(m>0\), 使 \(\|A x\| \geq m\|x\|, \forall x \in X\).
设 \(X\) 为 Banach空间, \(A \in \mathcal{L}(X)\), 且 \(\|A\|<1\), 则 \(I-A\) 是有界可逆的, 且 \[ (I-A)^{-1}=\sum_{n=0}^{\infty} A^n, \quad\left\|(I-A)^{-1}\right\| \leq \frac{1}{1-\|A\|}, \] 其中 \(A^0=I, I\) 是恒等算子.
对偶空间
如果\(X\)是数域\(C\)上的赋范线性空间,集合 \[ X^{\prime}=\mathcal{L}(X, C)=\left\{x^{\prime} \mid x^{\prime}: X \rightarrow C \text { 是连续线性泛函 }\right\} \] 规定:
- \(\left(x_1^{\prime}+x_2^{\prime}\right)(x)=x_1^{\prime}(x)+x_2^{\prime}(x)\),\((\lambda x')(x)=\lambda(x'(x))\)
- \(\left\|x^{\prime}\right\|=\sup _{\|x\| \leq 1}\left|x^{\prime}(x)\right|\)
称\(X'\)是\(X\)的对偶空间/共轭空间。
如果\(X\)可分,那么\(X'\)可分。
常见空间上的连续线性泛函
\(l^1\)空间
其上的连续线性泛函可以表现为: \[ f(x)=\sum_{k=1}^{\infty} \xi_k \eta_k, \forall x=\left\{\xi_k\right\} \in l^1 \] 就是序列中的各项按由\(f(x)\)唯一确定的权重\(y=\{\eta_i\}\)线性组合。且: \[ ||f(x)||=\sup|\eta_k|=||y||_{l^1} \]
\(l^p\)空间 \[ f(x)=\sum_{k=1}^{\infty} \xi_k \eta_k, \forall x=\left\{\xi_k\right\} \in l^1 \] 其中\(y\in l^q\),满足\(p^{-1}+q^{-1}=1\)。也就是说:\((l^p)'=l^q\)
\(L^p[a,b]\)空间: \[ f(x)=\int_a^b x(t) y(t) \mathrm{d} t, \forall x=x(t) \in L^p[a, b] \] 其中\(y=y(t)\in L^q[a,b]\),\(q=\frac{p}{p-1}\)。
内积空间和希尔伯特(Hilbert)空间
设 \(X\) 是数域 \(K\) (实或复数域)上的线性空间, 若 \(\forall x, y \in X\) 存在唯一的数 \((x, y) \in K\), 满足下列三条内积公理:
- 正定性: \((x, x) \geq 0,(x, x)=0 \Leftrightarrow x=\theta\);
- 对第一变元的线性性:\((\alpha x+\beta y, z)=\alpha(x, z)+\beta(y, z), \forall z \in X, \forall \alpha, \beta \in K\)
- 共轭对称性: \((x, y)=\overline{(y, x)}\),
则称 \((x, y)\) 为 \(x, y\) 的内积, \(X\) 为内积空间。如果是复内积空间,对第二变元有共轭线性,即: \[ (x, \alpha y+\beta z)=\bar{\alpha}(x, y)+\bar{\beta}(x, z) \] 两个向量内积为零,称为正交。如果一个集合\(\{x_i\}\)满足\((x_i,x_j)=\delta_{ij}\),称为正规正交集。
【勾股定理】 \(X\)是内积空间,\(x\)和\(y\)正交,则有: \[ \|x+y\|^2=\|x\|^2+\|y\|^2 \] 其中\(||x||=\sqrt{(x,x)}\)称为向量\(x\)的范数。
如果\(\{x_i\}\)是正规正交集,则\(\forall x\in X\) \[ \|x\|^2=\sum_{j=1}^n\left|\left(x, x_j\right)\right|^2+\left\|x-\sum_{j=1}^n\left(x, x_j\right) x_j\right\|^2 \] 【贝塞尔不等式】如果\(\{x_i\}\)是正规正交集,则\(\forall x\in X\) \[ \sum_{j=1}^n\left|\left(x, x_j\right)\right|^2 \leq\|x\|^2 \] 【柯西-施瓦茨不等式】 \[ |(x, y)| \leq\|x\| \cdot\|y\| \]
内积的性质
【连续性】内积对两个变元都是连续泛函。即\(x_n\to x,y_n\to y\)时,\((x_n,y_n)\to (x,y)\)
证明时先用三角不等式,再用柯西-施瓦茨不等式。 \[ \begin{aligned} \left|\left(x_n, y_n\right)-(x, y)\right| & \leq\left|\left(x_n, y_n\right)-\left(x_n, y\right)\right|+\left|\left(x_n, y\right)-(x, y)\right| \\ & =\left|\left(x_n, y_n-y\right)\right|+\left|\left(x_n-x, y\right)\right| \\ & \leq\left\|x_n\right\| \cdot\left\|y_n-y\right\|+\left\|x_n-x\right\| \cdot\|y\| \end{aligned} \]
【平行四边形公式】 \[ \|x+y\|^2+\|x-y\|^2=2\left(\|x\|^2+\|y\|^2\right) \] 如果赋范线性空间的范数满足这个式子,那么它可以成为内积空间,反之亦然。
【极化恒等式】 \[ (x, y)=\frac{1}{4}\left(\|x+y\|^2-\|x-y\|^2\right)+\frac{i}{4}\left(\|x+i y\|^2-\|x-i y\|^2\right) \]
希尔伯特空间
完备(所有基本列都是收敛的)的内积空间被称为希尔伯特空间。
\(n\)维实/复向量空间 \[ (x, y)=\bar{y}^{\mathrm{T}} x=\sum_{i=1}^n x_i \bar{y}_i \]
\(l^2\)平方可和序列空间 \[ (x, y)=\sum_{j=1}^{\infty} \xi_j \bar{\eta}_j \]
\(L^2[a,b]\)平方可积函数空间 \[ (x, y)=\int_a^b x(t) \cdot \bar{y}(t) \mathrm{d} t \]
正规正交基
【施密特正交化】对于任意线性无关组\(\{x\}\),有以下过程可以构造一个正规正交集: \[ \begin{aligned} & y_1=x_1 \Rightarrow e_1=\frac{y_1}{\left\|y_1\right\|} \\ & y_2=x_2-\left(x_2, e_1\right) e_1 \Rightarrow e_2=\frac{y_2}{\left\|y_2\right\|} \\ & y_3=x_3-\left(x_3, e_1\right) e_1-\left(x_3, e_2\right) e_2 \Rightarrow e_3=\frac{y_3}{\left\|y_3\right\|}, \cdots \\ & y_n=x_n-\sum_{i=1}^{n-1}\left(x_n, e_i\right) e_i \Rightarrow e_n=\frac{y_n}{\left\|y_n\right\|}, \cdots \end{aligned} \] 得到的正规正交集为\(\{e\}\),
【正规正交基】在希尔伯特空间中,不是任何其它正规正交集的子集的正规正交集,叫做正规正交基。
也即:在空间中,如果一个向量和正规正交基的每个元素都正交,那么这个向量是零向量。这说明了正规正交基的完全性。
设 \(H\) 为无穷维Hilbert空间, 则
- 若 \(H\) 可分, 则 \(H\) 有一个可数的正规正交基
- 每个非零的 \(H\) 都有正规正交基
设 \(S=\left\{e_\alpha\right\}_{\alpha \in \mathrm{A}}\) 是 \(H\) 的一个正规正交基, 则对 \(\forall x \in H\), 有
- 【傅里叶系数】\(x=\sum_{\alpha \in \mathrm{A}}\left(x, e_\alpha\right) e_\alpha\)
- 【帕塞瓦尔定理(勾股定理),完备性】\(\|x\|^2=\sum_{\alpha \in \mathbb{A}}\left|\left(x, e_\alpha\right)\right|^2\)
射影定理
【射影定理】 设 \(M\) 是Hilbert空间 \(H\) 中闭的线性子空间 则 \(\forall x \in H\), 必存在唯一的 \(y \in M, z \in M^{\perp}\), 使得 \[ x=y+z \] 其中\(y\)就是\(x\)在\(M\)上的射影。
【Frechet-Riesz表示定理】 设 \(H\) 是Hilbert空间, 对 \(\forall f \in H^*, \exists ! z_f \in H\), 使得 \(f(x)\) 可表示为 \[ f(x)=\left(x, z_f\right), \quad \forall x \in H, \] 并且 \(\|\boldsymbol{f}\|=\left\|z_f\right\|\).
例如,对\(R^3\)而言, \[ f(x)=a x_1+b x_2+c x_3=\vec{x} \cdot \vec{n} \] 其中 \(\vec{x}=\left\{x_1, x_2, x_3\right\}, \vec{n}=\{a, b, c\}\).要找的 \(z_f\) 就是 \(\vec{n}\), 它是平面 \(f(x)=0\) 的法向量.
巴拿赫(Banach)空间的基本定理
Hahn-Banach定理
【Hahn-Banach定理】 对于线性赋范空间 \(X\) 中线性子空间 \(G\) 上的连续线性泛函 \(f(x)\), 恒有 \(X\) 上的连续线性泛函 \(F(x)\), 使得 1. \(F(x)=f(x), x \in G\), 2. \(\|\boldsymbol{F}\|=\|f\|_G\).
【推论1】设 \(X\) 是线性赋范空间, 任给非零的 \(x_0 \in X\), 总存在 \(X\) 上的 连续线性泛函 \(f\), 满足 1. \(\|f\|=1\), 2. \(f\left(x_0\right)=\left\|x_0\right\|\).
【推论1的几何形式】 任意球面\(S\)上的任意一点\(x_0\),必定存在一个支撑超平面。
【推论2】设 \(X\) 是线性赋范空间, \(E\) 是 \(X\) 的闭子空间, \(x_0 \notin E\), 则存在 \(X\) 上的有界线性泛函 \(f\), 满足 1. \(f(x)=0, \forall x \in E\) 2. \(f\left(x_0\right)=d\), 3. \(\|f\|=1, d \triangleq \operatorname{dist}\left(x_0, E\right)>0\).
【Hahn-Banach定理的几何形式】若\(X\)中的线性流形\(g\)与开球\(B\)不相交,则有超平面\(H\)包含\(g\)且与\(B\)不相交
Banach逆算子定理
【纲集】可数个稀疏并叫第一纲集,不是第一纲的叫第二纲集。
完备距离空间是第二纲集。
【开映射定理】 设 \(X, Y\) 都是Banach空间, \(T \in \mathcal{L}(X, Y)\). 如果 \(\mathcal{R}(T)\) 是第二纲集, 则 \(T\) 为开映射.
【Banach逆算子定理】 设 \(X, Y\) 都是Banach空间, \(T \in \mathcal{L}(X, Y)\). 如果 \(T\) 既单又满, 则 \(T\) 是有界可逆的, 即 \(T^{-1} \in \mathcal{L}(Y, X)\).
【等价范数定理】设线性空间 \(X\) 上赋予了两个范数 \(\|\|_1,\|\|_2\), 它们都使 \(X\) 成为Banach空间, 如果 \(\|\cdot\|_1\) 强于 \(\|\cdot\|_2\), 则两个范数等价.
闭图像定理
【闭算子】 设 \(X, Y\) 是赋范线性空间, \(M\) 是 \(X\) 中的线性子空间, \(T: M \rightarrow Y\) 线性算子, \(M\) 称为 \(T\) 的定义域, 记为 \(\mathcal{D}(T)\). 如果由 \[ x_n \in \mathcal{D}(T), x_n \rightarrow x_0 \text {, 与 } T x_n \rightarrow y_0, \] 可推知 \(x_0 \in \mathcal{D}(T), T x_0=y_0\), 则称 \(T\) 为闭算子.
【图像】设 \(X, Y\) 是赋范线性空间, \(T: \mathcal{D}(T) \subset X \rightarrow Y\) 线性算子, 定义其图像为: \[ \mathcal{G}(T)=\{(x, y) \in X \times Y: x \in \mathcal{D}(T), y=T x\}, \]
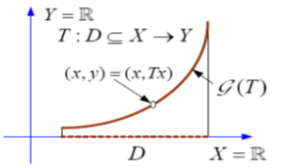
若对 \((x, y) \in X \times Y\), 引进范数 \[ \|(x, y)\|=\|x\|+\|y\| \text {. } \] 则 \(T\) 是闭算子 \(\Leftrightarrow \mathcal{G}(T)\) 是 \(X \times Y\) 中的闭集.
【闭图像定理】 设 \(X, Y\) 是Banach空间, \(T: X \rightarrow Y\) 闭算子, 则 \(T\) 为有界的.
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:

- 所有收敛列都是基本列是永远成立的。 ↩︎