数字信号处理·系统之章
你说得对,但是《数字信号处理》是电子信息工程学院独立开设的一门核心专业课,课程发生在一个被称作D221的幻想世界,在这里,被神选中的序列将被授予“傅里叶变换”,导引频域分解之力。玩家将扮演一位名为“DSP”的神秘角色,在自由的系统中邂逅性格各异、能力独特的信号们,和他们一起分析频谱,找回失散的频段——同时,逐步发掘“线性系统”的真相。
离散系统变换域分析
表示LTI系统有很多方法,我们常用三种:
- 单位脉冲响应 \(h[n]\)
- 单位脉冲响应的频谱密度函数(DTFT) \(H(e^{j\omega})\)
- 系统函数(单位脉冲响应的Z变换) \(H(z)\)
LTI系统的频域表示
特征函数和频率响应
对于LTI系统,对于某些输入序列,输出序列是输入序列和某个复常数的乘积。这样的输入序列叫做特征函数,复常数叫做系统的特征值。
由于输入序列为\(x[n]=e^{j\omega n}\)时,有 \[ y[n]=x[n]*h[n]=\sum_{k=-\infty}^\infty e^{j\omega(n-k)}h[k]=e^{j\omega n}H(e^{j\omega}) \] 所以LTI系统的其中一个特征函数就是\(x[n]=e^{j\omega n}\)(事实上,所有的指数型函数,例如\(5^n\)等,都是特征函数,而且,指数型函数和指数型函数的有限项乘积也是特征函数,但是形容\(e^{j\omega n}u[n]\)这种就不行),其对应的特征值为\(H(e^{j\omega})\)。
而且,由傅里叶变换,我们知道:序列\(x[n]\)往往可以表示为\(e^{j\omega n}\)的线性组合,即\(x[n]=\frac{1}{2\pi}\int_{-\pi}^\pi X(e^{j\omega})e^{j\omega n}d\omega\)。于是,我们将其中的每一项乘以对应的特征值,就得到了输出\(y[n]=\frac{1}{2\pi}\int_{-\pi}^\pi X(e^{j\omega})H(e^{j\omega})e^{j\omega n}d\omega\)。于是我们得到了: \[ Y(e^{j\omega})=X(e^{j\omega})H(e^{j\omega}) \] 如果LTI系统的相频响应满足\(\angle H(e^{j\omega})=-\omega n_d\),那么称这样的系统为线性相位系统。线性相位系统对所有频率分量\(e^{j\omega n}\)造成的延迟均为\(n_d\)。一般来说,我们用群延时衡量相位变化对信号的影响,有: \[ \tau(\omega)=-\frac{d}{d\omega}\angle H(e^{j\omega}) \] 如果群延时不是常数,那么会造成输出信号的失真,这称为色散。
LTI系统的Z变换分析
对于以下差分方程表示的系统: \[ y[n]=\sum_{k=1}^N a_ky[n-k]+\sum_{k=0}^Mb[k]x[n-k] \] 在有初始松弛条件(零状态)时,是因果LTI系统。其系统函数为: \[ H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^M b_kz^{-k}}{1-\sum_{k=1}^N a_kz^{-k}} \] 也可以把它表示为因式的形式: \[ H(z)=\frac{b_0}{a_0}\frac{\prod_{m=1}^M(1-c_mz^{-1})}{\prod_{n=1}^N (1-d_nz^{-1})} \] 关于系统的因果和稳定性,有如下结论:
- LTI系统是因果的 等价于 \(H(z)\)的收敛域包含无穷远点
- LTI系统是稳定的 等价于\(H(z)\)在单位圆上是收敛的
关于系统的零极点和幅频响应的关系,有如下结论:
- 对于单零点系统,零点为\(c\),当\(\omega=\theta_c\)时,幅频响应是极小值,零点越靠近单位圆,幅频响应的极小值越小,当零点在单位圆上时,这个极小值为\(0\)(如果采用对数坐标则为负无穷)
- 对于单极点系统,极点为\(d\),当\(\omega=\theta_d\)时,幅频响应是极大值,极点越靠近单位圆,幅频响应的极大值越大,当极点在单位圆上时,这个极大值为正无穷。极点在单位圆上或单位圆外,则系统不稳定。
有理系统的全通分解
幅频特性相同的系统
若有一个有理实系统,把其中的若干个零点或极点用它的共轭倒数代替,新系统的幅频响应和原来的系统相同。于是,如果设计好一个系统的幅频特性,一定存在符合要求的因果稳定LTI系统,其极点都在单位圆内。
全通系统
全通指的是\(|H(e^{j\omega})|\equiv1\)的系统,仅有相频特性随频率变化而变化。全通系统的零极点相对单位圆是镜像共轭成对的。也就是说:如果\(a_i\)是系统的零点,那么\((a_i^*)^{-1}\),即\(a_i\)的共轭的倒数,定是全通系统的极点。而且,对于有理实系数系统来说,零点和极点本身也是共轭成对的,即如果\(b_i\)是零点或极点,那么它的共轭一定也是零点或极点。
全通系统具有以下性质:
相位特性随频率单调下降,即 \[ \frac{\rm d\theta(\omega)}{\rm d\omega}<0 \]
输入信号\(x[n]\)和输出信号\(y[n]\)的能量相同,即 \[ \sum_{n=-\infty}^\infty\lvert x[n]\rvert^2=\sum_{n=-\infty}^\infty\lvert y[n]\rvert^2 \]
当频率\(\omega\)从\(0\)变化到\(\pi\)时,\(N\)阶全通系统的相位改变为\(N\pi\)
全通系统的应用主要在作相位均衡器,或者通过级联全通系统的方法提高系统的稳定性。
最小相位系统
对于一个离散时间因果稳定系统,它的极点都在单位圆内。如果在此基础上,零点也都在单位圆内,那么这样的系统叫做最小相位系统[3];如果零点全在单位圆外,叫最大相位系统;如果零点在单位圆内外都有,叫混合相位系统。
最小相位系统有以下性质:
- 在所有幅频响应相同的因果稳定系统中,最小相位系统的相位延迟最小
- 在所有幅频响应相同的实系数因果稳定系统中,最小相位系统的群延时最小
- 最小相位系统的逆系统也是最小相位系统
【例】因果序列\(x[n]\)的\(z\)变换为 \[ X(z)=\frac{\left(1-\frac 12 z^{-1}\right)\left(1-\frac 14 z^{-1}\right)\left(1-\frac 15 z\right)}{\left(1-\frac 16 z\right)} \] 又已知\(\alpha^nx[n]\)是一个最小相位系统,求\(\alpha\)的范围。
【解】只有不在单位圆内的有一个零点\(5\)和一个极点\(6\)。记\(y[n]=\alpha^nx[n]\),则有 \[ Y(z)=\sum_{n=-\infty}^\infty\alpha^nx[n]z^{-n}=X\left(\frac z\alpha\right) \] 如果\(a_i\)是\(X(z)\)的零点或极点,那么\(a_i\cdot\alpha\)就是\(Y(z)\)的零点或极点。为了让\(Y(z)\)的所有零极点都在单位圆内,只需调整\(\alpha\),让\(6\alpha\)在单位圆内即可。于是有: \[ \alpha<\frac 16 \]
有理系统的全通分解
任何有理系统函数都可以分解为最小相位系统\(H_{min}(z)\)和全通系统\(H_{ap}(z)\)级联的形式。假设系统仅有一个单位圆外的零点\((c^*)^{-1}\),即: \[ H(z)=H_1(z)(z^{-1}-c^*) \] 则\(H_1\)的零极点都在单位圆内,是最小相位系统。上式可以进一步表示为: \[ H(z)=H_1(z)(z^{-1}-c^*)\frac{1-cz^{-1}}{1-cz^{-1}}=H_1(z)(1-cz^{-1})\frac{z^{-1}-c^*}{1-cz^{-1}} \] 其中\(\frac{z^{-1}-c^*}{1-cz^{-1}}\)的零点是\((c^*)^{-1}\),极点是\(c\),互为共轭倒数,是全通系统,记作\(H_{ap}(z)\)。因为\(|z|<1\),其余部分是最小相位系统,记作\(H_{min}(z)\),于是分解完成。
上述过程的实质是在单位圆外零点\((c^*)^{-1}\)的共轭倒数\(c\)的位置放置了一个零点和一个极点。\(c\)上的极点和\((c^*)^{-1}\)这个零点一起构成了全通系统;\(c\)上的极点和原来系统的其它零极点构成了最小相位系统。
【例】把以下系统分解成全通系统和最小相位系统的级联 \[ H(z)=\frac{1-3z^{-1}}{1+\frac 12 z^{-1}} \] 【解】该系统有\(z=-1/2\)的极点和\(z=3\)的零点。即\((c^*)^{-1}=3\),得\(c=1/3\)。则有: \[ \begin{align} H(z)&=\frac{-3}{1+\frac 12 z^{-1}}\left(z^{-1}-\frac 13\right)\\ &=-3\left(\frac{1-\frac 13z^{-1}}{1+\frac 12 z^{-1}}\right)\left(\frac{z^{-1}-\frac 13}{1-\frac 13z^{-1}}\right) \end{align} \] 于是: \[ H_{min}(z)=-3\left(\frac{1-\frac 13z^{-1}}{1+\frac 12 z^{-1}}\right) \]
\[ H_{ap}(z)=\left(\frac{z^{-1}-\frac 13}{1-\frac 13z^{-1}}\right) \]
广义线性相位系统
我们之前所说的经典频响是这样的: \[ H(e^{j\omega})=|H(e^{j\omega})|e^{j\angle H(e^{j\omega})} \] 这时\(|H|\)叫经典幅频响应,\(\angle H\)叫经典相频响应.但是现在我们引入广义响应: \[ H(e^{j\omega})=A(e^{j\omega})e^{j\varphi(\omega)} \] 这时候,\(A\)叫做“广义幅频响应”,而\(\varphi\)叫做“广义相频响应”。请注意“经典”和“广义”的不同:经典幅频响应永远是正的,而广义相频响应可以是负的。因此,广义相频响应和经典相频响应,在\(A\)变成负数的时候,会有一个\(\pi\)的差距。
所谓的线性相位的意思是,系统对不同频率的正弦信号所产生的相移和正弦信号的频率呈线性关系。即: \[ \angle H(e^{j\omega})=-\alpha \omega \] 那么广义线性相位的意思就是,给这个加上一个常数,变成 \[ \angle H(e^{j\omega})=\beta-\alpha \omega \] 经过一番数学推导,相频响应满足上面式子的系统的单位脉冲响应满足以下等式: \[ \sum_{n=-\infty}^\infty h[n]\sin(\omega(n-\alpha)+\beta)=0 \] 满足上面式子的情况的两组解如下:
- \(\beta=0\)或\(\pi\),\(2\alpha=M\in \mathbb N\),\(h[2\alpha-n]=h[n]\)
- \(\beta=\pi/2\)或\(3\pi/2\),\(2\alpha=M\in \mathbb N\),\(h[2\alpha-n]=-h[n]\)
于是,我们可以分出四种广义线性相位系统。
第I类广义线性相位系统
该类系统满足\(h[M-n]=h[n]\),即\(h[n]\)关于\(M/2\)偶对称,而且\(M\)是偶数。第I类的\(\beta=0,\pi\)。所以相频响应是过原点的直线,斜率是\(-M/2\),群延时是\(M/2\)。
这类系统的广义幅频响应\(A(e^{j\omega})\)关于\(\omega=m\pi,m\in \mathbb Z\)偶对称,可用作各种滤波器。
第II类广义线性相位系统
该类系统满足\(h[M-n]=h[n]\),即\(h[n]\)关于\(M/2\)偶对称,而且\(M\)是奇数。第II类的\(\beta=0,\pi\)。所以相频响应是过原点的直线,斜率是\(-M/2\),群延时是\(M/2\)。
这类系统的广义幅频响应\(A(e^{j\omega})\)关于\(\omega=2m\pi,m\in \mathbb Z\)偶对称,关于\(\omega=(2m+1)\pi,m\in \mathbb Z\)奇对称,幅度函数在\(\pi\)时为零,不适合作高通、带阻滤波器。
第III类广义线性相位系统
该类系统满足\(h[M-n]=-h[n]\),即\(h[n]\)关于\(M/2\)奇对称,而且\(M\)是偶数。第III类的\(\beta=\pi/2,3\pi/2\)。所以相频响应是不过原点的直线(过\((0,\pi/2)\)或\((0,3\pi/2)\)),斜率是\(-M/2\),群延时是\(M/2\)。
这类系统的广义幅频响应\(A(e^{j\omega})\)关于\(\omega=m\pi,m\in \mathbb Z\)奇对称,只适合作带通滤波器。
第IV类广义线性相位系统
该类系统满足\(h[M-n]=-h[n]\),即\(h[n]\)关于\(M/2\)奇对称,而且\(M\)是奇数。第IV类的\(\beta=\pi/2,3\pi/2\)。所以相频响应是不过原点的直线,斜率是\(-M/2\),群延时是\(M/2\)。
这类系统的广义幅频响应\(A(e^{j\omega})\)关于\(\omega=2m\pi,m\in \mathbb Z\)奇对称,关于\(\omega=(2m+1)\pi,m\in \mathbb Z\)偶对称,幅度函数在\(\pi\)时为零,不适合作低通、带通滤波器。
由于第3、4类广义线性系统的相移特性,可以作希尔伯特变换器使用。
对于广义线性系统而言,如果\(z_0\)是系统的零点,那么\(z_0^{-1},z_0^*,(z_0^*)^{-1}\)也是系统的零点。第2、3类的零点一定包含-1,第3、4类的零点一定包含1.
信号的采样和重建
连续信号的理想采样
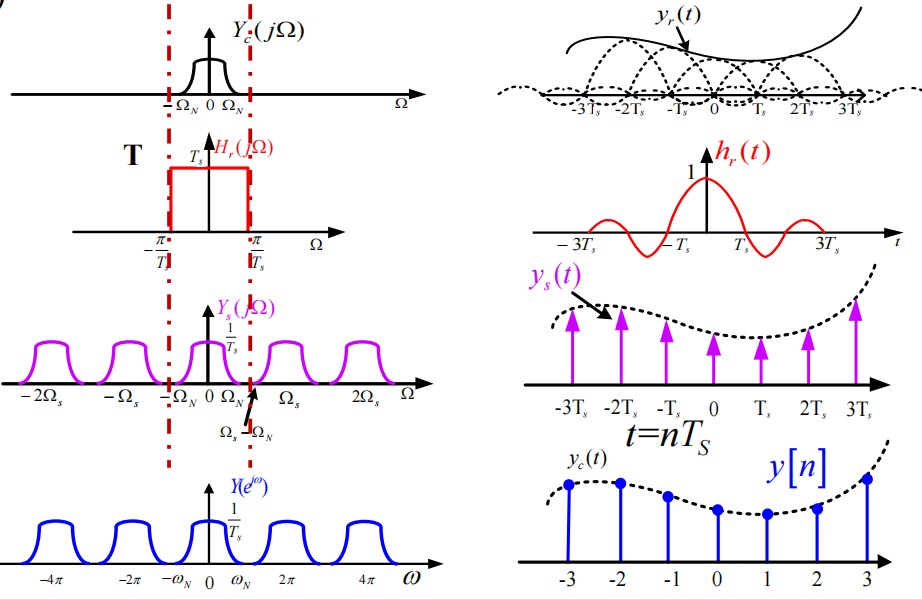
设原连续信号为\(x_c(t)\),用来采样的理想冲击串为\(s(t)\),采样得的连续采样信号为\(x_s(t)\),采样得的离散时间序列为\(x[n]\)。其中采样用的理想冲击串的周期为\(T_s\)。
\(X_s\)和\(X_c\)的关系
这一部分是《信号与系统》的内容,这里只简单提一下。
首先我们知道,冲击串的傅里叶变换还是冲击串,即: \[ S(j\Omega)=\frac{2\pi}{T_s}\sum_{k=-\infty}^{\infty}\delta(\Omega-k\Omega_s) \] 由傅里叶变换的乘积性质,有: \[ X_s(j\Omega)=\frac 1 {T_s}\sum_{k=-\infty}^\infty X_c(j\Omega-jk\Omega_s) \] 即:\(x_s(t)\)的频谱\(X_s(j\Omega)\)是连续时间信号\(x_c(t)\)的频谱\(X_c(j\Omega)\)以采样周期\(\Omega_s=2\pi/T_s\)的周期延拓,并以\(\frac 1{T_s}\)加权的结果。所以,为了不使得频域混叠,需满足\(\Omega_s>2\Omega_N\),其中\(\Omega_N\)是原信号所含有的最高频分量的频率。
\(X(e^{j\omega})\)和\(X_c(j\Omega)\)的关系
有: \[ X_s(j\Omega)=\sum_{n=-\infty}^{\infty}x[n]e^{-j\Omega nT_s} \] 令\(\omega=\Omega T_s\),有: \[ X_s\left(j\frac{\omega}{T_s}\right)=\sum_{n=-\infty}^\infty x[n]e^{-j\omega n} \]
可以发现:使用\(1/T_s\)对\(X_c(j\Omega)\)加权且频率按\(\Omega=\omega/T_s\)尺度变换,得到函数\(X_c(j\omega/T_s)/T_s\),将其以\(2\pi\)为周期进行延拓,得离散序列\(x[n]\)频谱\(X(e^{j\omega})\).
连续信号的理想重建
重建系统的示意图如下:
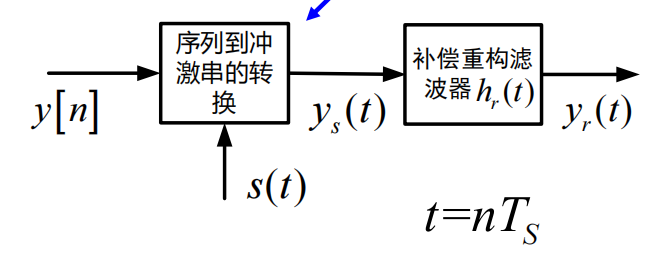
先把离散时间信号序列\(y[n]\)转化为连续时间信号\(y_s(t)\),然后让\(y_s(t)\)经过截止频率为\(\pi/T_s\),幅度\(T_s\)的低通滤波器,得到重建信号\(y_r(t)\)。
即: \[ H_r(j\Omega)=\begin{cases} T_s, &|\Omega|<\frac{\Omega_s}{2}\\ 0 , &\text{others} \end{cases} \]
余弦信号的采样
这一段没有什么新东西,主要内容是以对余弦信号采样举例来让人直观感受“频域混叠”的存在,尤其是在采样频率\(\Omega_s=2\Omega_0\)时,可能会出现各种情况:当\(\varphi=0\)时,才能恢复原信号;当其它情况时,都不能恢复原信号,极端时刻,甚至采样值全部为0,不包含任何信息。
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:

- 也就是说最小相位系统的意思就是零极点都在单位圆内。 ↩︎