实变泛函·实变函数之章
[toc]
实变函数和泛函分析是一门广度极强的学科,融合了分析、代数、抽代、拓扑等数学各个方面的知识。在学习时要能建立起各个概念之间的联系。
点集
\(R^n\)中的线性运算、内积和范数
\(n\)维欧氏空间\(R^n\)
\(R^n\)指的是\(n\)维向量组成的集合: \[ R^n=\{(x_1,x_2,\cdots,x_n):x_i\in R,i=1,2,\cdots n\} \] 在这个集合上定义加法和数乘: \[ \begin{aligned} &\forall x,y\in R^n,\lambda\in R\\ &x+y=(x_1+y_1,x_2+y_2,\cdots,x_n+y_n)\\ &\lambda x=(\lambda x_1,\lambda x_2,\cdots,\lambda x_n) \end{aligned} \] 其满足所谓的“线性运算八条性质”:对任意的\(x,y\in R^n;\lambda,\mu\in R\)
- \(x+y=y+x\)
- \(x+y+z=(x+y)+z=x+(y+z)\)
- \(x+0=x\);
- \(x+(-x)=0\)
- \(1x=x\)
- \(\lambda(x+y)=\lambda x+\lambda y\)
- \((\lambda+\mu) x=\lambda x+\mu x\)
- \((\lambda \mu) x=\lambda(\mu x)\)
对于\(\forall x,y\in R^n\),定义内积: \[ (x,y)=\sum_{i=1}^n x_iy_i \] 内积满足以下三条性质:对于任意的\(x,y,z\in R^n\),任意的\(\lambda,\mu\in R\),有:
- 正定性:\((x,x)\geq 0\)
- 对称性:\((x,y)=(y,x)\)
- 对第一变元的线性:
- \((x+y,z)=(x,z)+(y,z)\)
- \((\lambda x,y)=\lambda(x,y)\)
定义了内积的\(n\)维向量空间被称为“内积空间”,也叫“欧几里得空间”.
对于一般的内积空间\(X\),总成立柯西-施瓦茨不等式: \[ |(x,y)|\leq ||x||\cdot||y|| \] 其中\(||x||=\sqrt{(x,x)}\),称之为向量的范数。范数满足以下三条性质:
- 正定性:\(||x||\geq 0\),取到\(0\)当且仅当\(x=0\)
- 齐次性:\(||\lambda x||=|\lambda|\cdot ||x||\)
- 三角不等式:\(||x+y||\leq||x||+||y||\)
其实,只要\(f(x)\)满足以上三个条件,那么它就可以被称作范数,范数不只有上面所提到的那一种定义。
对三角不等式的证明可以先对式子两边取平方,再运用柯西-施瓦茨不等式。
如果\(x,y\in R^n\)且\(x,y\neq 0\) ,则存在实数\(\theta\in[0,\pi]\),满足: \[ \cos \theta=\frac{(x,y)}{||x||\cdot ||y||} \] 这个实数称为两个向量之间的夹角。
最后,我们定义两点间的距离:\(d(x,y)=||x-y||\)。距离的本质是范数,满足范数的性质。
\(R^n\)中点列的极限
设\(\{x_k\}\)是\(R^n\)中的点列,如果\(\forall \epsilon>0,\exists N,\forall k>N,||x_k-a||<\epsilon\),称\(\{x_k\}\)收敛于\(a\),记作: \[ \lim_{n\to \infty}x_k=a \] 点列的极限满足以下四条性质:
- 点列的极限如果存在,那么唯一
- 收敛点列必定有界
- \(\lim_{k\to \infty}(x_k+y_k)=a+b\)
- \(\forall \lambda \in R,\lim_{k\to \infty} (\lambda x_k)=\lambda a\)
点列收敛等价于点列的每个分量都收敛(即按分量收敛)。
\(R^n\)中点集的基本概念和性质
\(a\in R^n,r>0\),则称集合\(\{x\in R^n:||x-a||<r\}\)称为以\(a\)为心,\(r\)为半径的“开球”或者“球形邻域”,记作\(B_r(a)\).
令\(\bar B_r(a)=\{x\in R^n:||x-a||\leq r\}\),称作“闭球”
令\(B_r^o(a)=\{x\in R^n:0<||x-a||<r\}\),称作“去心开球”
若\(E\subset R^n,\exists r>0,s.t. E\subset B_r(0)\),称\(E\)是有界的。否则,称\(E\)是无界的。
点
如果\(a\in E,\exists r>0,s.t. B_r(a)\subset E\),则\(a\)叫做\(E\)的内点,如果\(a\)是\(E^c\)(\(E\)的补集)的内点,那么\(a\)叫做\(E\)的外点。如果\(a\)对\(E\)来说既不是内点,也不是外点,那么\(a\)叫做\(E\)的边界点。
换句话说:以\(a\)为心的任意邻域内都存在属于\(E\)的点,同时也存在不属于\(E\)的点,那么\(a\)叫做\(E\)的边界点。
如果以\(a\)为心的任意球形邻域中都含有\(E\)的无限多个点,那么\(a\)叫做\(E\)的聚点,也叫极限点。聚点的定义可以简化,也就是说,只要以\(a\)为心的任意球形邻域中都含有\(E\)中不同于\(a\)的一个点,那么\(a\)就是\(E\)的聚点。很显然,这两种说法实际上是等价的。还有一种等价的说法:从\(E\)中选出互不相同的点组成点列\(\{x_k\}\),如果\(\lim_{k\to \infty}x_k=a\),那么\(a\)是\(E\)的聚点。\(E\)中不是聚点的点叫做孤立点。
关于各种点之间的关系,有如下的结论:
- 内点一定是聚点,外点一定不是聚点
- 聚点可以是内点,也可以是边界点,但不可能是外点
- 孤立点一定是边界点
- 边界点是聚点或孤立点
- 如果一个点既不是聚点,也不是边界点,那么一定是外点
- 内点必属于集合,外点必不属于集合,边界点不一定属于集合
我们会发现:聚点不一定在集合内,例子很简单:对于\(R^1,E=Q,e=\lim_{k\to \infty}(1+1/n)^n,e\notin E\)
设\(A\subset R^n,\forall x\in R^n,\exist r,s.t. \exist a\in A,a\in B_r(x)\),那么称\(A\)在\(R^n\)中稠密。稠密等价于以下两个结论:
- 对\(\forall x\in R^n\),总存在\(A\)中的点列收敛于\(x\)。
- \(R^n\)中的点要么是\(A\)中的点,要么是\(A\)的聚点。
开集
点集\(E\)的全体内点的集合叫做\(E\) 的内部,记作\(E^o\)。如果\(E=E^o\),那么称\(E\)为开集。
几个经典的开集:空集、\(R^n\)、数轴上的开区间、\(\{(x,y)|y>0\}\)、开球
任意多个开集的并还是开集,有限个开集的交还是开集
闭集
如果\(E\subset R^n\)是开集,那么\(E^c\)叫做闭集。
几个经典的闭集:数轴上的闭区间、\(R^2\)的横轴和下半平面、有限个点的集合、开球的补
集合可以既不是开集也不是闭集。
任意个闭集的交还是闭集,有限个闭集的并还是闭集。
点集\(E\subset R^n\)的全体聚点的集合叫做\(E\)的导集,记作\(E'\)。如果\(\bar E=E\cup E'\),那么\(\bar E\)叫做\(E\)的闭包。
如果\(E\)是闭集,那么它的闭包是它自己。
内部是含于一个集合的最大开集,闭包是包含一个集合的最小闭集。
\(R^n\)中的基本定理
我们在学实数的时候经常提“六大定理”,即:
- 确界存在定理
- 单调数列收敛定理
- 有界数列必有收敛子列
- 柯西收敛准则
- 闭区间套定理
- 有限覆盖定理
在\(R^n\)中,前两个定理不再成立,后面的继续成立。
\(R^n\)中的有界点列必有收敛子列,也就是:任何无穷点集都含有聚点
如果\(\{x_k\}\)是\(R^n\)中的点列,如果\(\forall \varepsilon>0,\exists N=N(\varepsilon)>0,s.t. \forall k,l>N,||x_k-x_l||<\varepsilon\),称\(\{x_k\}\)是基本列。“是基本列”和“收敛”等价。
设\(\{E_k\}\)是一个闭集列,都不是空集,而且:
- 后一项是前一项的子列
- \(\lim _{k\to \infty} diam(E_k)=0\)
那么存在唯一的\(\xi \in \bigcap_{k=1}^{\infty} E_k\),其中\(diam(A)=\sup_{\forall x,y\in A}||x-y||\)。
设\(E\in R^n,\{G_\alpha\}_{\alpha \in \Gamma}\)是\(R^n\)中的一个开集族,如果\(E\subset \bigcup G_\alpha\),称\(\{G\}\)是\(E\)的一个开覆盖。\(R^n\)中的有界闭集的任意一个开覆盖都有有限子覆盖
距离
点\(x\)和集合\(B\)的距离为: \[ d(x,B)=\inf\{d(x,y):y\in B\} \] 意思就是点到集合中每个点的距离的下确界
两个集合之间的距离为: \[ d(A,B)=\inf\{d(x,y):x\in A,y\in B\} \] 意思就是从集合里面任选两个点,它们之间的距离的下确界
有以下结论:
- 如果A是非空闭集,则\(\exists y\in A,s.t.d(x,y)=d(x,A)\)
- 如果AB是非空闭集,则\(\exists x\in A,y\in B,s.t. d(x,y)=d(A,B)\)
- \(F_1,F_2\)是不相交的非空闭集,则存在\(R^n\)上的连续函数,使得
- \(0\leq f(x)\leq 1\)
- \(f(x)=0,x\in F_1\);\(f(x)=1,x\in F_2\)
康托尔(Cantor)三分集
把\([0,1]\)三等分,去掉中间的一部分,再把左右两个剩下的三等分,再各自去掉中间的一部分,重复无限次,剩下来的集合就是Cantor三分集(P)。
它:
- 是闭集,完备集
- 没有内点
- 是疏朗集,即\(\bar P\)(闭包)没有内点
- 基数是连续势
- 测度为零,外测度也为零
康托尔函数\(\theta(x)\):把在构造康托尔集的过程中第\(n\)次去掉的\(2^{n-1}\)个开区间上依次取值为 \[ \frac {1}{2^n},\frac{3}{2^n},\cdots,\frac{2^n-1}{2^n} \] 规定\(\theta(0)=0,\theta(1)=1\)
康托尔函数是\([0,1]\)上的单调不减连续函数。
测度论
测度是“长度”、“面积”概念的扩展。
集合的测度\(m:E\to[0,+\infty]\)应当满足:
非负性
正则性:若\(I=(a,b)\),则\(m(I)=b-a\)
可数可加性:如果集合\(E_1,E_2\cdots\)都有测度且两两不交,那么: \[ m\left(\bigcup_{k=1}^\infty E_k \right)=\sum_{k=1}^\infty m(E_k) \]
这里主要讨论勒贝格测度。在定义测度时,先定义勒贝格外测度,然后在其基础上诱导出一个可测集合类,在其上的外测度就是一种期望的测度。
外测度
对于\(R^n\)的子集\(E\),定义非负广义函数: \[ m^*(E)=\inf \left\{ \sum_{k=1}^\infty |I_k|:I_1,I_2\cdots\text{是开矩体,且}E\subset \bigcup_{k=1}^\infty I_k\right\} \] 开矩体是\(n\)个开区间的直积,其体积为每个开区间的长度之积。
外测度有以下性质:
非负性
单调性:如果\(E_1\subset E_2\),则\(m^*(E_1)\leq m^*(E_2)\)
次可数可加性:如果集合\(E_1,E_2\cdots\)都有测度且两两不交,那么: \[ m^*\left(\bigcup_{k=1}^\infty E_k \right)\leq \sum_{k=1}^\infty m^*(E_k) \]
平移不变性: \[ m^*(E+\{a\})=m^*(E) \] 其中\(E+\{a\}=\{x+a,x\in E\}\)
可测集
定义,如果\(E,T\in R^n\): \[ m^*(T)=m^*(T\cap E)+m^*(T\cap E^c) \] 则称\(E\)是勒贝格可测集,简称为可测集。此时\(m^*(E)\)称为\(E\)的测度,记作\(m(E)\)。这个等式叫做卡特西奥多里条件。
这个条件可以等价于: \[ m^*(T)\geq m^*(T\cap E)+m^*(T\cap E^c) \] 设\(R^n\)上的可测集所构成的集族称为M,则:
- 空集属于M
- 如果\(E\)可测,那么\(E^c\)可测
- 如果\(E_1,E_2\in M\),则它们的并、交、差都是可测
- 可测集的有限并也可测,而且满足可列可加
区间可测,凡是开集或闭集都可测,外测度为零的集合可测且测度为零
零测集的子集、至多可数个零测集的并也是零测集。
不可测集
存在不可测集。
可测函数
可测函数的定义和性质
设\(f(x)\)是定义在可测集\(E\subset R^n\)上的广义实值函数,若\(\forall a\in R\),\(E(f>a)\)(即\(\{x\in E:f(x)>a\}\))都是可测集,则称\(f(x)\)为可测函数。
以下条件相互等价:
- \(f(x)\)是可测函数,即\(\forall a\in R,E(f> a)\)可测
- \(\forall a\in R,E(f\geq a)\)可测
- \(\forall a\in R,E(f< a)\)可测
- \(\forall a\in R,E(f\leq a)\)可测
如果\(f(x)\)在可测集\(E\)上是可测函数,那么在\(E\)的每个可测子集上也是可测函数。
如果\(E=\bigcup_{k=1}^\infty E_k\),其中每一个\(E_k\)都是可测集而且\(f(x)\)在其上可测,那么\(f(x)\)在\(E\)上可测。
可测函数类关于确界、上下极限封闭。即:如果\(\{f_k\}\)都是可测集\(E\)上的函数,那么\(\sup_k f_k(x),\inf_k f_k(x),\overline{\lim}_{k\to \infty}f_k(x),\underline{\lim}_{k\to \infty}f_k(x)\)都可测。
可测函数类关于加、减、乘、除、数乘、绝对值封闭。
如果\(P(x)\)是一个和集合\(E\)中元素\(x\)有关的命题,如果存在一个\(E\)的零测子集\(M\),使得\(P(x)\)在\(E/M\)上恒成立,称\(P(x)\)在\(E\)上几乎处处成立,记作\(a.e.\)
如果\(f(x),g(x)\)都是\(E\)上的广义实值函数,且\(f(x)=g(x)\ a.e. x\in E\),那么\(f(x)\)可测是\(g(x)\)可测的充要条件。
下面定义三种函数:
设\(X=R\)的一个子集\(E\),称: \[ \chi_E(x)=\begin{cases} 1 & x\in E\\ 0 & x\in E^c \end{cases} \] 为\(E\)上的特征函数。如果\(E\)可测,那么它的特征函数可测。
如果\(f(x)\)的定义域\(E\)可以分为有限个不相交的集合\(E_k\),且\(f(x)\)在每个\(E_k\)上取常值\(c_k\),那么称\(f(x)\)是\(E\)上的简单函数。(简单理解:取有限个实数)
如果在简单函数的定义的基础上,每个\(E_k\)都是矩体,称\(f(x)\)为阶梯函数。
可测函数和简单函数的关系(简单函数逼近定理)
如果\(f(x)\)是可测集\(E\subset R\)上的非负可测函数,当且仅当存在非负可测渐升简单函数列\(\{\phi_k(x)\}\),使得: \[ \lim_{k\to \infty}\phi_k(x)=f(x) \] 如果\(f(x)\)在\(E\)上有界,那么上述收敛是一致的。
事实上,作简单函数列\(\phi_k(x)\),使得: \[ \phi_k(x)=k\chi_{F_k}(x)+\sum_{i=1}^{k2^k}\frac{i-1}{2^k}\chi_{E_{ki}}(x) \] 其中 \[ E_{ki}=E\left(\frac{i-1}{2^k}\leq f<\frac i{2^k}\right),F_k=E(f\geq k) \] 即满足上述定理的要求。
如果\(f(x)\)是可测集\(E\)上的可测函数,当且仅当存在可测的简单函数列\(\{f_k(x)\}\),满足:
- \(|f_k(x)|\leq|f(x)|\)
- \(\lim_{k\to \infty}f_k(x)=f(x)\)
如果\(f(x)\)在\(E\)上有界,那么上述收敛是一致的。
在证明时,可以把\(f(x)\)分解成正负部之差,利用前面关于非负函数的定理,令 \[ f_k(x)=\phi^+_k(x)-\phi^-_k(x) \]
可测函数的收敛
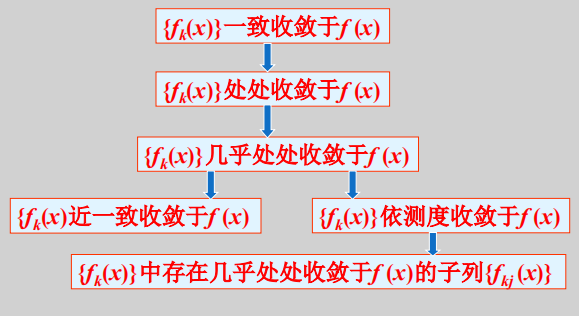
设\(f(x),f_k(x)\)都是定义在\(E\)上的可测函数,有:
处处收敛:\(\forall \epsilon>0,\forall x\in E,\exists K=K(x,\epsilon)\)当\(k>K\)时,有:\(|f_k(x)-f(x)|<\epsilon\),记作 \[ \lim_{k\to \infty}f_k(x)=f(x) \]
几乎处处收敛:存在一个零测集,使得\(f_k(x)\)在\(E\)中除了这个零测集以外的点上收敛于\(f(x)\)
一致收敛:\(\forall \epsilon>0,\forall x\in E,\exists K=K(\epsilon)\)当\(k>K\)时,有:\(|f_k(x)-f(x)|<\epsilon\)。一致收敛等价于: \[ \lim_{k\to \infty}\sup_{x\in E}|f_k(x)-f(x)|=0 \]
有Egoroff(叶洛果夫)定理:设\(m(E)< \infty\),如果\(\{f_k\}\)在\(E\)上几乎处处收敛,那么对于任意的\(\delta > 0\),有\(E\)的可测子集\(E_\delta,m(E_\delta)<\delta\),使得\(\{f_k\}\)在\(E/E_\delta\)上一致收敛。也就是说,几乎处处收敛的函数列是“近一致收敛”的。
例如,对于函数列\(\{f_k=x^k\}\),\(E=[0,1]\),其处处收敛于 \[ f(x)=\begin{cases} 0,&x\in[0,1)\\ 1,&x=1 \end{cases} \] 因 \[ \beta_k=\sup_{x\in E}|f_k-f|=1 \] 不趋向于\(0\),所以它不是一致收敛的。然而只要去掉任意小的区域,把\(E\)变成\([0,1-\delta]\),那么就一致收敛了。
其实还有比几乎处处收敛更弱的收敛,叫做依测度收敛。如果\(\{f_k\},f\)是可测集\(E\)上的几乎处处有限的函数,如果对任意\(\varepsilon>0\),有: \[ \lim _{k \rightarrow \infty} m\left(\left\{x \in E:\left|f_k(x)-f(x)\right|>\varepsilon\right\}\right)=0 \] 即:\(f_k\)与\(f\)的差值比\(\varepsilon\)大的集合的测度趋向于0,那么说\(\{f_k\}\)依测度收敛于\(f\)。
几乎处处收敛比依测度收敛更强,是因为几乎处处有限可以推出依测度收敛,反之不然。
如果函数列依测度收敛,那么存在函数列的子列\(\{f_{k_i}\}\)几乎处处收敛,这叫做Riesz定理。
如果\(f\)是可测集\(E\)上的几乎处处有限的函数,\(\forall \delta>0,\exists F,m(E/F)<\delta\),使得\(f(x)\)在闭集\(F\)上连续,这叫做鲁津定理。
有关可测函数的常见结论和各种收敛的关系总结如下:
- 可测函数与零测集无关.
- 可测函数是简单函数列处处收敛的极限.(当可测函数有界时, 可做到一致收敛)
- 可测函数关于一些运算的封闭性.
- 可测集 \(E\) 上的连续函数是可测的.
- 可测集 \(E\) 上的简单函数是可测的.
- \(R\) 中可测集 \(E\) 上的单调函数是可测的.
勒贝格积分
首先我们从简单函数出发:假设\(\varphi(x)\)是\(E\subset R\)上的非负简单函数,在\(E_i\)上取值\(c_i\),且\(E=\bigcup E_i,E_i\cap E_j=\emptyset\)。也就是说: \[ \varphi(x)=\sum_{i=1}^p c_i\chi_{E_i}(x) \] 那么定义\(\varphi(x)\)在\(E\)上的勒贝格积分(下简称为L积分)为: \[ \int _E\varphi(x)dx=\sum_{i=1}^p c_im(E_i) \] 根据简单函数逼近定理,我们可以把这个定义扩展到非负可测函数上:如果\(f(x)\)是\(E\)上的非负可测函数,那么定义\(f(x)\)的L积分: \[ \int_E f(x)dx=\sup_{\varphi(x)\leq f(x),x\in E}\left\{ \int_E \varphi(x)dx\right\} \] 其中\(\varphi(x)\)是\(E\)上的非负可测简单函数。如果有: \[ \int_E f(x)dx<\infty \] 就称\(f(x)\)是\(E\)上可积的。
进一步,因为每个可测函数都可以分解成两个非负可测函数的差(即正部和负部),有: \[ f(x)=f^+(x)-f^-(x) \] 定义可测函数上的L积分: \[ \int _Ef(x)dx=\int_Ef^+(x)dx-\int_E f^-(x)dx \]
L积分的性质
L积分的条件
以下,记\(L(E)\)为在\(E\)上L可积的函数构成的集合。
- 【必要条件】:\(f(x)\in L(E)\to f(x)\)在\(E\)上几乎处处有界
- 【充分条件】:\(f(x)\)是\(E\)上的有界可测函数,\(m(E)<+\infty\),则\(f(x)\in L(E)\)
- 【充分条件】:\(f(x)\)是\(E\)上的可测函数,\(g(x)\in L(E),|f(x)|<g(x)\),则\(f(x)\in L(E)\)
L积分的基本性质
线性,保序性
略,和黎曼积分(以下简称R积分)相同
有限可加性
如果\(f(x)\in L(E)\),那么\(f(x)\)在\(E\)的子集上也L可积。
如果\(E=A\cup B,A\cap B=\emptyset,AB\)可测,那么 \[ \int_E f(x)dx=\int_Af(x)dx+\int_Bf(x)dx \]
集合意义
如果\(f(x)\)是\(E\subset R^n\)上的非负实值函数,称: \[ \underline{G}(f)=\underline{G}_E(f)=\left\{(x, y) \in R^{n+1}: x \in E, 0 \leq y \leq f(x)\right\} \] 为\(f(x)\)在\(E\)上的下方图形,如果\(f(x)\)在\(E\)上可测,那么他的下方图形在\(R^{n+1}\)上也可测,有: \[ m(\underline{G}(f))=\int_E f(x) d x \] 如果\(E\)可测,则\(G(f)\)在\(R^{n+1}\)上可测,\(f(x)\)也 可测,且也有上面的结论
L积分的特殊性质
零测集上任何函数L积分为零,更进一步,如果两个函数只在一个零测集上有区别,那么这两个函数的L积分相等
函数\(f(x)\)L可积和其绝对值\(|f(x)|\)L可积等价,且积分的绝对值不大于绝对值的积分
绝对连续性:如果\(f(x)\in L(E)\),则\(\forall \varepsilon >0,\exists \delta>0,s.t. \forall e\in E,m(e)<\delta\),有: \[ \left|\int_e f(x) \mathrm{d} x\right| \leq \int_e|f(x)| \mathrm{d} x<\varepsilon \]
如果一个函数R可积,那么它L可积,且两个积分的值相等。
这说明,R积分的有关问题,可以转换为L积分,再利用马上就要说明的L积分的优良性质完成 。
L积分的优良性质
【勒贝格收敛控制定理】如果\(\{f_k(x)\}\)是\(E\in R^n\)上的可测函数列,且:
- \(\lim _{k\to \infty}f_k(x)=f(x)\)
- \(\exists F(x)\in L(E),\forall k,|f_k(x)|\leq F(x)\ a.e.x\in E\)
那么,\(f_k(x),f(x)\in L(E)\),且积分和极限可以交换次序,有: \[ \lim _{k \rightarrow \infty} \int_E f_k(x) \mathrm{d} x=\int_E f(x) \mathrm{d} x=\int_E \lim _{k \rightarrow \infty} f_k(x) \mathrm{d} x . \]
相比之下,黎曼积分需要函数列一致收敛,才能交换顺序。一致收敛是一个非常强的条件。
推论:如果\(\{f_k(x)\}\)是\(E\in R^n\)上的可测函数列,且:
- \(\lim _{k\to \infty}f_k(x)=f(x)\)
- \(\exists M>0,|f_k(x)|\leq M,a.e. x\in E\)
- \(m(E)<\infty\)
那么,\(f_k(x),f(x)\in L(E)\),且积分和极限可以交换次序,有: \[ \lim _{k \rightarrow \infty} \int_E f_k(x) \mathrm{d} x=\int_E f(x) \mathrm{d} x=\int_E \lim _{k \rightarrow \infty} f_k(x) \mathrm{d} x . \] 推论:设\(u_i(x)\in L(E)\),且有: \[ \sum_{i=1}^{\infty} \int_E\left|u_i(x)\right| d x<+\infty \] 则:
\(\sum_{i=1}^n u_i(x)\)几乎处处收敛
其和函数\(f(x)\in L(E)\),且 \[ \int_E f(x) \mathrm{d} x=\int_E\left[\sum_{i=1}^{\infty} u_i(x)\right] \mathrm{d} x = \sum_{i=1}^{\infty} \int_E u_i(x) d x \]
【例】求 \[ \lim _{n \rightarrow \infty}(R) \int_0^1 \frac{n x}{1+n^2 x^2} \sin n x d x \]
【解】因为原函数列不一致收敛,因此需要用L积分。
验证勒贝格收敛控制定理: \[ \left|f_n(x)\right| \leq\left|\frac{n x}{1+n^2 x^2}\right| \leq \frac{n x}{2 n x}=\frac{1}{2} \stackrel{\Delta}{=} F(x), x \in[0,1] \]
则有: \[ \begin{aligned} & \lim _{n \rightarrow \infty}(R) \int_0^1 \frac{n x}{1+n^2 x^2} \sin n x d x \\ & =\lim _{n \rightarrow \infty}(L) \int_{[0,1]} \frac{n x}{1+n^2 x^2} \sin n x d x \\ & =(L) \int_{[0,1]}\left(\lim _{n \rightarrow \infty} \frac{n x}{1+n^2 x^2} \sin n x\right) d x \\ & =(L) \int_{[0,1]} 0 \mathrm{~d} x=0 . \end{aligned} \]
有时候,问题中并不显式地出现极限、求和符号,但是可以通过把被积分展开成级数的和,再求解:
【例】 \[ \int_{0}^1 \frac{\ln(1-x)}{x}dx \] 【解】
首先展开成级数: \[ \frac{\ln (1-x)}{x}=-\sum_{n=1}^{\infty} \frac{x^{n-1}}{n}, x \in[0,1) \]
我们发现这不是一致收敛的,但是没关系,我们有勒贝格积分: \[ \begin{aligned} &\ (R) \int_0^1 \frac{\ln (1-x)}{x} \mathrm{~d} x \\ & =(L) \int_{[0,1]} \frac{\ln (1-x)}{x} \mathrm{~d} x \\ & =(L) \int_{[0,1]}\left(-\sum_{n=1}^{\infty} \frac{x^{n-1}}{n}\right) \mathrm{d} x\\ & =-\sum_{n=1}^{\infty}(L) \int_{[0,1]} \frac{x^{n-1}}{n} d x \\ & =-\sum_{n=1}^{\infty} \frac{1}{n^2} \\ & =-\frac{\pi^2}{6} \end{aligned} \]
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
