关于离散系统和Z变换的那些事
离散系统和Z变换,与连续系统和Laplace变换很像,但也有些不同,可以对比学习。 本文合计5598字。
@[toc]
离散时间信号与系统
常用基本序列
单位样值序列(对应冲激函数) \[ \delta(n)=\begin{cases} 1 & n=0\\\\ 0 & \text{others} \end{cases} \] 于是,仿照把任意信号分解成冲激函数和的形式,我们可以把任意序列分解成单位样值序列的和的形式,并且这个操作比在连续函数里更直观,即: \[ x(n)=\sum_{m=-\infty}^{\infty} x(m)\delta(n-m) \]
单位阶跃序列(对应单位阶跃函数) \[ u(n)=\begin{cases} 1 & n\geq 0\\\\ 0 & n<0 \end{cases} \] 类似于单位冲激函数和单位阶跃函数的关系,有: \[ u(n)=\sum_{m=-\infty}^{n}\delta(m) \] 和单位阶跃函数不同,\(u(0)\)有明确定义,为\(1\).
矩形序列
矩形序列\(G_N(n)\)指的是从0开始(含0),含\(N-1\)个\(1\)的序列,即: \[ G_N(n)=\begin{cases} 1 & n\in[0,n)\\\\ 0 & \text{others} \end{cases} \] 矩形序列是两个单位阶跃序列的组合。有: \[ G_N(n)=u(n)-u(n-N) \]
(单边)指数序列 \[ x(n)=a^nu(u) \] 当\(|a|<1\)时收敛,\(|a|>1\)和\(a=-1\)时发散。
当\(a<0\)时会在\(x\)轴两侧摆动。
正弦序列
正弦序列是由正弦函数采样的序列,有: \[ x(n)=A\sin(\omega t+\varphi)|_{t=nT_s}=A\sin(\omega nT_s+\varphi) \] 其中\(T_s\)是采样周期。定义数字角频率: \[ \Omega=\omega T_s \] 与正弦函数不同,正弦序列不一定是周期序列。当且仅当 \[ \frac{2\pi} {\Omega} \] 是有理数时,正弦序列才是周期序列。
离散序列基本运算
一般的运算和连续信号(函数)没有多少区别。需要注意的是压扩运算。压扩运算需要去除某些点,或者补充某些0点。
离散时间系统
离散时间系统的描述和连续时间系统差别不大。不同于连续时间系统中常用积分器,离散时间系统中常用延时器,其符号为一个方框中写了一个“D”,作用是输入\(x(n)\),输出\(x(n-1)\)。
记忆与无记忆、线性与非线性、时变与时不变、稳定与不稳定的含义和连续时间系统没有区别。
差分方程时域求解方法
离散时间系统的数学表达式常用差分方程来表示,一般差分方程的形式为: \[ a_0y(n)+a_1y(n-1)+\cdots+a_Ny(n-N)=b_0x(n)+b_1x(n-1)+\cdots+b_My(n-M) \] 求解的过程和微分方程类似:首先将方程右边置0求得齐次解;然后根据激励信号的特点选取含待定系数的特解,代入方程求得特解;再将齐次解和特解相加得完全解;最后代入 初始条件 求待定系数。
求齐次解
将方程右边置0,得: \[ \sum_{k=0}^Na_ky(n-k)=0 \] 特征方程为: \[ \sum_{k=0}^Na_k\lambda^{N-k}=0 \] 这是一个关于\(\lambda\)的多项式方程。求解特征方程得到特征根\(\lambda_1\cdots\lambda_N\)。
如果\(\lambda_i\)是单根或者共轭复根,那么齐次解中含有一项: \[ C_i\lambda_i^n \] 如果\(\lambda_j\)是\(r\)重根,那么齐次解中含有项: \[ C_1n^{r-1}\lambda_j^n+C_2n^{r-2}\lambda_j^n+\cdots+C_{r-1}n\lambda_j^n+C_r\lambda_j^n \]
选取特解
常见激励和它对应的特解如下:
激励\(x(n)\) 特解 说明 \(n^m\) \(\sum_{i=0}^m P_{m-i}n^{m-i}\) 所有特征根不为1 \(n^m\) \(n^r\sum_{i=0}^m P_{m-i}n^{m-i}\) 1是\(r\)重特征根 \(\lambda^n\) \(P\lambda^n\) \(\lambda\)不是特征根 \(\lambda^n\) \(P_1n\lambda^n+P_0\lambda^n\) \(\lambda\)是特征单根 \(\lambda^n\) \(\sum_{i=0}^rP_{r-i}n^{r-i}\lambda^n\) \(\lambda\)是\(r\)重特征根 \(\sin(\beta n)\)或\(\cos(\beta t)\) \(P\cos(\beta n)+Q\sin(\beta n)\) 或 \(A\cos(\beta n-\theta)\) 其中\(Ae^{j\theta}=P+jQ\),\(e^{\pm j\theta}\)不是特征根
【例】求解差分方程 \[ y(n)+3y(n-1)+2y(n-2)=x(n) \] 其中激励为\(x(n)=2^n,n\geq 0\), 起始条件 为\(y(-2)=\frac12,y(-1)=0\)。
【解】特征方程为: \[ \lambda^2+3\lambda+2=0 \] 特征根为 \[ \lambda_1=-1,\lambda_2=-2 \] 则齐次解为 \[ y_h(h)=C_1(-1)^n+C_2(-2)^n \] 由于\(x(n)=2^n\),2不是特征根,选特解形式为 \[ y_p(n)=P\cdot2^n \] 代入方程,有: \[ P\cdot2^n+3P\cdot2^{n-1}+2P\cdot 2^{n-2}=2^n \] 两边同时除以\(2^n\),有: \[ 3P=1 \] 得特解: \[ y_p(n)=\frac 13\cdot2^n \] 则完全解形式为: \[ y(n)=C_1(-1)^n+C_2(-2)^n+\frac 13\cdot 2^n \] 代入初始条件.因为方程右边的激励只在\(n\geq0\)处有定义,我们要把已知的\(y(-1),y(-2)\)转换成\(y(0),y(1)\).有: \[ \begin{cases} y(0)+3y(-1)+2y(-2)=x(0)\\\\ y(1)+3y(0)+2y(-1)=x(1) \end{cases} \] 得: \[ y(0)=0,y(1)=2 \] 将上述条件代入完全解形式,得: \[ \begin{cases} C_1+C_2+\frac 13=0\\\\ -C_1-2C_2+\frac 23=1 \end{cases} \] 于是可解得完全解: \[ y(n)=\frac 23(-1)^n -(-2)^n +\frac 13 \cdot2^n \ \ n\geq 0 \]
零输入和零状态响应
零输入响应
零输入响应就是只考虑起始状态,而把输入置0时,系统的响应。也就是 \[ \begin{cases} \sum_{i=0}^N a_iy_{zi}(n-i)=0\\\\[2ex] y_{zi}(-1)=y(-1)\\\\ y_{zi}(-2)=y(-2)\\\\ \cdots\\\\ y_{zi}(-N)=y(-N) \end{cases} \] 的解。其中\(y_{zi}\)表示零输入(Zero Input)。
零状态响应
零状态响应的意思是起始状态全为0,仅仅考虑外加激励,所引起的响应。也就是 \[ \begin{cases} \sum_{i=0}^N a_iy_{zs}(n-i)=\sum_{i=0}^N b_ix(n-i)\\\\ y(-1)=y(-2)=\cdots=0 \end{cases} \] 其中\(y_{zs}(n)\)表示零状态(Zero State)。
可以通过零输入响应和零状态响应求和的办法求解全响应。
【例】求解差分方程 \[ y(n)+3y(n-1)+2y(n-2)=x(n) \] 其中激励为\(x(n)=2^n,n\geq 0\),初始条件为\(y(0)=1,y(1)=2\)。
【解】特征方程为: \[ \lambda^2+3\lambda+2=0 \] 特征根为 \[ \lambda_1=-1,\lambda_2=-2 \] 则齐次解为 \[ y_h(n)=C_1(-1)^n+C_2(-2)^n \] 因为初始条件包含了激励信号的影响,因此需要求出起始条件为: \[ y(-2)=\frac12,y(-1)=0 \] 则有: \[ \begin{cases} C_1(-1)^{-1}+C_2(-2)^{-1}=0\\\\ C_1(-1)^{-2}+C_2(-2)^{-2}=\frac 12\\\\ \end{cases} \] 解得零输入响应为: \[ y_{zi}(n)=(-1)^n-2(-2)^n \] 然后求零状态响应。由于\(x(n)=2^n\),2不是特征根,选特解形式为 \[ y_p(n)=P\cdot2^n \] 代入方程,有: \[ P\cdot2^n+3P\cdot2^{n-1}+2P\cdot 2^{n-2}=2^n \] 两边同时除以\(2^n\),有: \[ 3P=1 \] 得特解: \[ y_p(n)=\frac 13\cdot2^n \] 则零状态响应的形式为: \[ y_{zs}(n)=D_1(-1)^n+D_2(-2)^n+\frac 13 \cdot 2^n \]
因为求解的是零状态响应,因此此时系统的初始条件为:\(y(-1)=y(-2)=0\)。代入差分方程,得初始条件: \[ y_{zs}(0)=0,y_{zs}(1)=1 \] 代入待定系数,解得: \[ y_{zs}(n)=-\frac 13(-1)^n+(-2)^n +\frac 13 \cdot (2^n) \] 则全响应为 \[ \begin{aligned} y(n)&=y_{zi}(n)+y_{zs}(n)\\\\ &=\frac 23(-1)^n -(-2)^n +\frac 13 \cdot2^n \ \ n\geq 0 \end{aligned} \]
单位样值响应
单位响应就是激励信号是\(\delta(n)\)时的零状态响应。它具有齐次解的形式,而且具有固定起始条件,即: \[ h(-N+1)=0,h(-N+2)=0,\cdots,h(0)=1 \]
【例】求以下系统的单位样值响应 \[ y(n)+3y(n-1)+2y(n-2)=2x(n-1)+x(n-2) \] 【解】先求系统 \[ y(n)+3y(n-1)+2y(n-2)=x(n) \] 的单位样值响应\(h_1\),再由线性时不变特性求\(h(n)\).
齐次解的形式为: \[ h_1(n)=[C_1(-1)^n+C_2(-2)^n]u(n) \] 代入固定起始条件\(h(-1)=0,h(0)=1\): \[ \begin{cases} -C_1-\frac 12 C_2=0\\\\ C_1+C_2=1 \end{cases} \] 得: \[ h_1(n)=[(-1)^(n+1)+2(-2)^n]u(n) \] 有: \[ \begin{aligned} h(n)&=2h_1(n-1)+h_1(n-2)\\\\ &=2[(-1)^n+2(-2)^{n-2}]u(n-1)+[(-1)^{n-1}+2(-2)^{n-2}]u(n-2)\\\\ &=\frac {\delta(n)}2+(-1)^nu(n)-1.5(-2)^nu(n) \end{aligned} \]
卷积和
两个序列\(x(n)\)和\(h(n)\)的“卷积和”定义如下: \[ y(n)=x(n)\bigotimes h(n)=\sum_{m=-\infty}^\infty x(m)h(n-m) \] 卷积和具有交换律、结合律、分配律,此外,还有:
移不变性 \[ x_1(n-m)\bigotimes x_2(n+k)=y(n-m+k) \]
序列和单位样值序列的卷积 \[ x(n)\bigotimes h(n-m)=x(n-m) \]
序列和单位阶跃序列的卷积 \[ x(n)\bigotimes u(n)=\sum_{i=-\infty}^n x(n) \]
在计算两个有限长度序列的卷积时,可以像列乘法竖式一样,先把两个序列右对齐,然后算“乘法”(只是不进位),即:
- 两序列右对齐
- 逐个样值对应相乘,不进位
- 同列乘积相加
得到的结果\(y(n)\)的第一个数的下标是两个原始序列的第一个数的下标的和。
对于无穷长序列一般只能通过定义公式计算。
离散时间信号与系统变换域分析
\(Z\)变换
类似于拉普拉斯变换,Z变换也分为双边和单边。
双边\(Z\)变换的定义如下: \[ X(z)={\mathscr Z}[x(n)]=\sum_{n=-\infty}^\infty x(n)z^{-n} \] 单边\(Z\)变换的定义如下: \[ X(z)={\mathscr Z}[x(n)]=\sum_{n=0}^\infty x(n)z^{-n} \]
那么为什么和拉普拉斯变换这么像呢?这是因为\(Z\)变换可以从拉普拉斯变换导出。
考虑对一个连续时间信号\(x(t)\)进行时间间隔为\(T\)的理想冲激抽样,抽样所得的信号记为\(x_s(t)\),则有: \[ x_s(t)=x(t)\cdot \delta_T(t)=\sum_{n=-\infty}^\infty x(nT)\delta(t-nT) \] 对上式取\(Z\)变换,有: \[ X_s(s)={\mathscr L}[x_s(t)]=\int_{0}^{\infty}\left[\sum_{n=-\infty}^\infty x(nT)\delta(t-nT)\right]e^{-st} {\mathbf d}t \] 对调积分求和、利用冲激函数性质,有: \[ X_s(s)=\sum_{n=-\infty}^\infty x(nT)e^{-snT} \] 设\(z=e^{sT}\),由于\(T\)是给定常数,则\(z\)是\(s\)的函数,则有: \[ X_s(z)=\sum_{n=-\infty}^\infty x(nT)z^{-n} \] 在一般的离散系统中,让\(T=1\),则有: \[ X_s(z)=\sum_{n=-\infty}^{\infty} x(n)z^{-n} \] 一个序列的\(Z\)变换,实际上是一个系数为这个序列的样值,变量为\(z^{-1}\)的幂级数。即: \[ X(z)=\cdots+x(-2)z^2+x(-1)z^1+x(0)z^0+x(1)z^{-1}+x(2)z^{-2}+\cdots \]
\(Z\)变换的收敛域
既然是从拉普拉斯变换导出来的,而且还是幂级数,那就不得不讨论收敛域。
复习一下,分析里面判断级数收敛有很多方法,其中最常用的有达朗贝尔判别法,即对于变号级数, \[ \lim_{n\to \infty} \left|\frac{x(n+1)z^{-(n+1)} } {x(n)z^{-n} }\right|=\rho \] 如果\(\rho<1\),那么绝对收敛;如果\(\rho>1\),那么发散。
结合拉普拉斯变换,我们把序列分成左边序列,右边序列,双边序列来讨论。由于 \[ z=e^{s} \] 我们可以通过下图的方法来建立S平面和Z平面的联系。
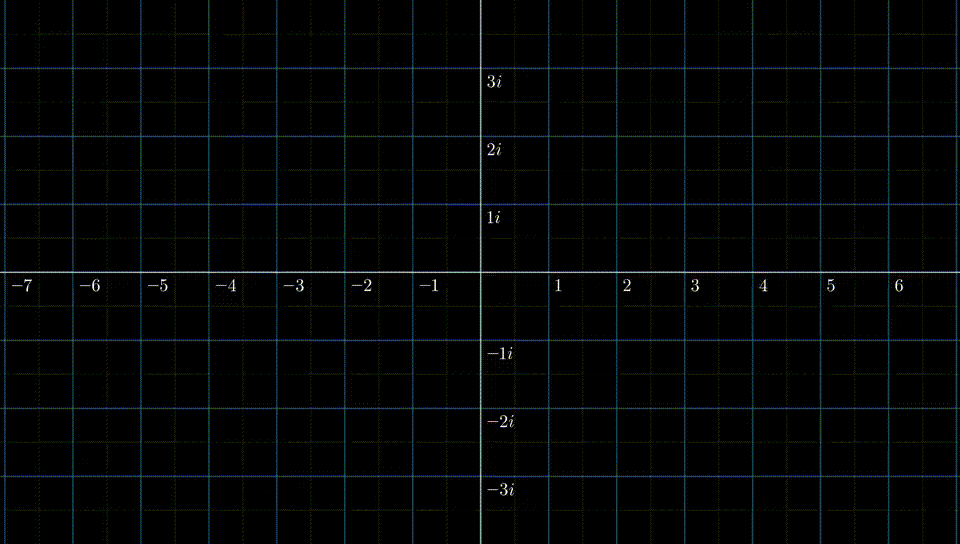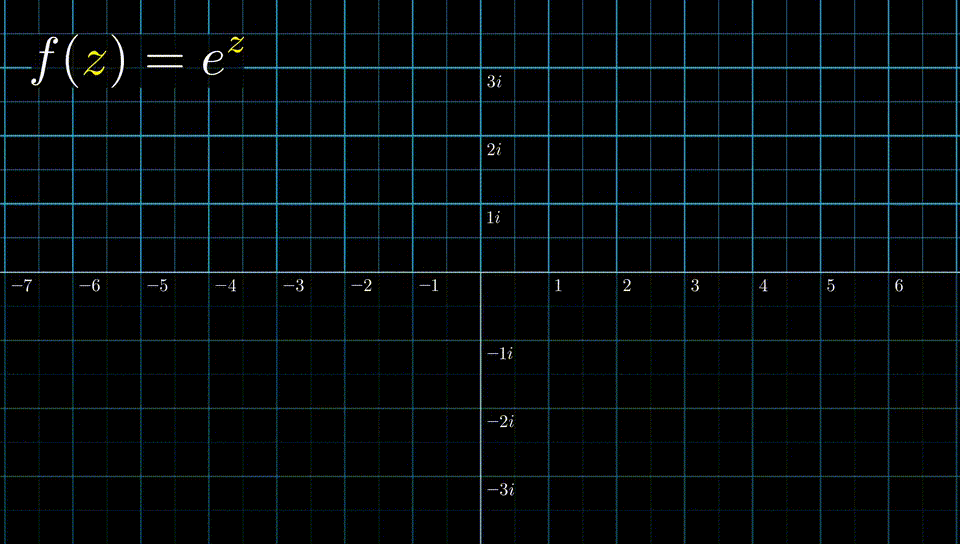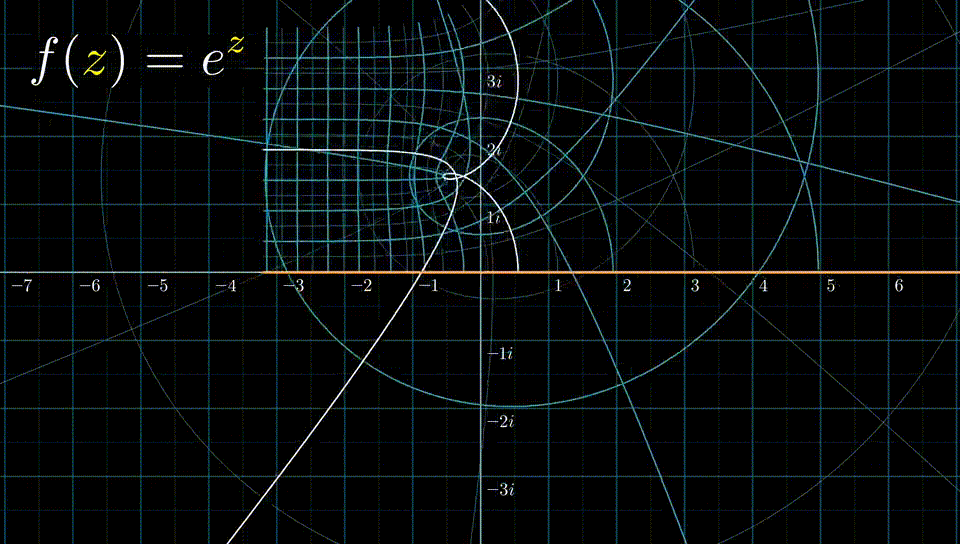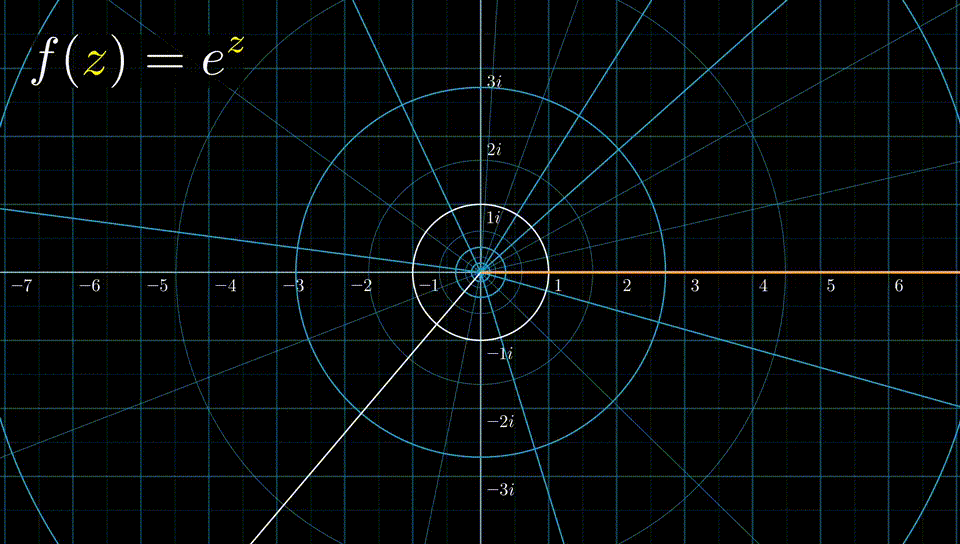
有:
| 序列(函数)类型 | Z变换收敛性形状 | 拉普拉斯变换收敛域形状 |
|---|---|---|
| 右边 | 以原点为中心的圆之外 \(\|z\|>\|a\|\) | 右半平面 \(Re[s]>\alpha\) |
| 左边 | 以原点为中心的圆之内 \(\|z\|<\|b\|\) | 左半平面 \(Re[s]<\beta\) |
| 两边 | 以原点为圆心的圆环 \(\|z\|\in(a,b)\) | 条带 \(Re[s]\in (\alpha,\beta)\) |
对于有限长的序列,收敛域是除去零点和无穷远点的整个Z平面。
常见序列的\(Z\)变换
| 序列名称 | 序列表达式 | \(Z\)变换 | 收敛域 |
|---|---|---|---|
| 单位样值序列 | \(\delta(n)=(n=0)?1:0\) | \(1\) | 全平面 |
| 单位阶跃序列 | \(u(n)=(n\geq 0)?1:0\) | \(\frac{z} {z-1}\) | \(\|z\|>1\) |
| 因果指数序列 | \(x(n)=a^nu(n)\) | \(\frac{z} {z-a}\) | \(\|z\|>\|a\|\) |
\(Z\)变换的性质
设 \[ {\mathscr Z}[x(n)]=X(z),|z|\in(\alpha,\beta) \]
时域性质
反褶性质 \[ {\mathscr Z}[x(-n)]=X(z^{-1}),|z|\in(\frac 1\beta,\frac 1\alpha) \]
扩展性质 \[ {\mathscr Z}\left[x\left(\frac na \right)\right]=X(z^a),|z|\in (\alpha^{\frac 1a},\beta ^{\frac 1a}) \]
位移性质
单边
若\(x(n)\)是双边序列,有: \[ {\mathscr Z}[x(n)u(n)]=X(z) ,|z|>a \] 则有: \[ {\mathscr Z}[x(n+m)u(n)]=z^m\left[ X(z)-\sum_{k=0}^{m-1} x(k)z^{-k} \right]\\\\ {\mathscr Z}[x(n-m)u(n)]=z^{-m}\left[ X(z)+\sum_{k=-m}^{-1} x(k)z^{-k} \right]\\\\ \] 请注意这里的“位移”:\(x(n-m)u(n)\)和拉普拉斯变换里的“位移”\(f(t-t_0)u(t-t_0)\),以及傅里叶变换里的“位移”\(f(t-t_0)\)的区别。
特别的,如果\(x(n)\)是因果序列,那么有: \[ \begin{aligned} {\mathscr Z}[x(n+m)u(n)]&=z^m\left[ X(z)-\sum_{k=0}^{m-1} x(k)z^{-k} \right]\\\\ {\mathscr Z}[x(n-m)u(n)]&=z^{-m}X(z) \end{aligned} \]
双边
双边位移性质比较简单。 \[ {\mathscr Z}[x(n\pm m)]=z^{\pm m}X(z),|z|\in(\alpha,\beta) \]
线性性质
频域性质
\(Z\)域微分-序列线性加权 \[ {\mathscr Z}[n\cdot x(n)]=-z\frac{ {\mathbf d}X(z)} { {\mathbf d}z} \]
\(Z\)域压扩-序列指数加权 \[ {\mathscr Z}[a^n x(n)]=X\left(\frac za\right),\alpha<\left|\frac za\right|<\beta \] 特殊的,如果要实现\(Z\)域反褶运算,有: \[ {\mathscr Z}[(-1)^nx(n)]=X(-z) \]
其它性质
时域卷积 \[ {\mathscr Z}[x_1(n)\bigotimes x_2(n)]=X_1(z)X_2(z) \]
初值定理
对于因果序列 \[ x(0)=\lim_{z\to \infty} X(z) \]
终值定理 \[ x(\infty)=\lim_{z\to 1}[(z-1)X(z)] \]
利用\(Z\)变换性质求其它常用序列的\(Z\)变换
单位样值序列的平移\(\delta(n-m)\)
由时移性质,有: \[ {\mathscr Z}[\delta(n-m)]=z^{-m} \]
斜变序列\(x(n)=nu(n)\)
由\(Z\)域微分-线性加权性质,有: \[ {\mathscr Z}[nu(n)]=-z\frac{ {\mathbf d} } {\mathbf dz}\left(\frac {z} {z-1}\right)=\frac{z} {(z-1)^2} \]
因果余弦序列\(x(n)=\cos(\omega_0 n)u(n)\)
由欧拉公式: \[ \cos(\omega_0 n)=\frac 12 \left(e^{j\omega_0n}+e^{-j\omega_0 n}\right) \] 和已知的公式 \[ {\mathscr Z}[\left(e^{\pm j\omega_0}\right)^nu(n)]=\frac{z} {z-e^{\pm j\omega_0} },|z|>1 \] 结合线性性质,得 \[ {\mathscr Z}[\cos(\omega_0 n)u(n)]=\frac{z^2 -z\cos(\omega_0)} {z^2-2z\cos \omega_0+1},|z|>1 \] 同理,因果正弦序列为: \[ {\mathscr Z}[\sin(\omega_0 n)u(n)]=\frac{z\sin(\omega_0)} {z^2-2z\cos \omega_0+1},|z|>1 \]
逆\(Z\)变换的求解
一般的线性时不变系统的\(Z\)变换表达式往往具有有理多项式的形式。
长除法
长除法的意思就是根据\(Z\)变换的定义,直接求解幂级数的系数,从而求解原始序列。
当收敛域形式为\(|z|>a\)时,幂级数表现出洛朗级数的形式,序列是右边序列,此时应把分母整理成降幂形式,再做长除法。
当收敛域形式为\(|z|<b\)时,幂级数表现出泰勒级数的形式,序列是左边序列,此时应把分母整理成升幂形式,再做长除法。
这种长除法只能得到序列的部分样值,而且多用于单边\(z\)变换。对于双边\(z\)变换,一般用部分分式展开法。
部分分式分解法
部分分式分解法的核心思想是把有理多项式分式分解成基本分式 \[ \frac{kz} {z-a} \] 的和,然后由于 \[ {\mathscr Z}^{-1}\left[\frac{kz} {z-a}\right]=ka^nu(n),|z|>a \] 或者 \[ {\mathscr Z}^{-1}\left[\frac{kz} {z-a}\right]=-ka^nu(-n-1),|z|<a \] 来求解原始序列。
【例】求解: \[ {\mathscr Z}^{-1}\left[\frac{5z} {-3z^2+7z-2}\right] \] 分收敛域为:(1) \(|z|>2\) (2) \(|z|\in (\frac 13 , 2)\)两种情况。
【解】首先对 \[ \frac{X(z)} {z}=\frac{5} {-3z^2+7z-2} \] 进行分解,过程略,如果不会请参考拉普拉斯变换部分相关内容。有: \[ \frac{X(z)} {z}=\frac{-1} {z-2}+\frac{1} {z-\frac{1} {3} } \] 则: \[ X(z)=\frac{-z} {z-2}+\frac{z} {z-\frac{1} {3} } \]
收敛域为\(|z|>2\)
此时,有: \[ x(n)=-2^nu(n)+\left(\frac 13\right)^nu(n) \]
收敛域为\(|z|\in \left(\frac 13,2\right)\)
这时要考虑两个分式分别代表的收敛域是什么。因为线性组合的收敛域是各项的收敛域的交集。我们经分析,得:第一项对应收敛域\(|z|<2\),第二项对应收敛域\(|z|>\frac 13\)。(如果反过来,那么收敛域就是空集,这和题目不符),因此: \[ x(n)=2^nu(-n-1)+\left(\frac 13\right)^nu(n) \]
对于右边序列,如果出现共轭复根的情况,即 \[
\frac{kz} {z^2+a}
\] 则有 \[
\begin{aligned}
\frac{kz} {z^2+a}&=\frac{\frac{k} {\sqrt a}\cdot \frac{z} {\sqrt a}
} {\left(\frac z{\sqrt a}\right)^2+1}\\\\
&=\frac{k} {\sqrt a}\frac{\frac{z} {\sqrt a}\sin \frac \pi 2}
{\left(\frac z{\sqrt a}\right)^2-2\left(\frac z{\sqrt a}\right)\cos\frac
\pi 2 +1}\\\\
&\to \frac{k} {\sqrt a}\cdot \sqrt{a}^n\cdot \sin\left(\frac{\pi}
{2}n\right)u(n)
\end{aligned}
\] 可以使用mathematica验证上述推导,输入:
1 | |
输出: \[ \frac{k z} {a+z^2} \] 对于2阶重极点,有: \[ {\mathscr Z}^{-1}\left[\frac{kz} {(z-a)^2}\right]=a^{n-1}knu(n) \] 对于更高阶的极点,有: \[ {\mathscr Z}\left[\frac{kz} {(z-a)^r}\right]=\frac{k} {(r-1)!}a^{n-r+1}\prod_{i=0}^{r-2}(n-i)=k a^{n-r+1} \binom{n} {r-1} \]
用\(Z\)变换求解差分方程
一般差分方程的形式如下: \[ \sum_{k=0}^N a_ky(n-k)=\sum_{r=0}^M b_rx(n-r) \] 对等式两边取\(Z\)变换: \[ \sum_{k=0}^N a_kz^{-k}\left[Y(z)+\sum_{l=-k}^{-1}y(l)z^{-l}\right]=\sum_{r=0}^M b_rz^{-r}\left[X(z)+\sum_{m=-r}^{-1}x(m)z^{-m}\right] \] 则系统全响应(的\(Z\)变换)为: \[ Y(z)=\frac{\sum_{r=0}^M b_rz^{-r}\left[X(z)+\sum_{m=-r}^{-1}x(m)z^{-m}\right]} {\sum_{k=0}^Na_kz^{-k} }-\frac{\sum_{k=0}^N\left[a_kz^{-k}\cdot\sum_{l=-k}^{-1}y(l)z^{-l}\right]} {\sum_{k=0}^Na_kz^{-k} } \] 其中第一项代表零状态响应,第二项代表零输入响应。
......麻了没?这么多分式,\(\sum\),我打着都麻。其实这玩意很简单的,下面通过一个例题给大家表演一下。
【例】差分方程 \[ y(n)+3y(n-1)+2y(n-2)=x(n) \] 其中激励为\(x(n)=2^n,n\geq 0\), 起始条件 为\(y(-2)=2,y(-1)=0\)。求零输入、零状态和全响应。
【解】对方程两边取\(Z\)变换,有: \[ Y(z)+3\left[z^{-1}Y(z)+y(-1)\right]+2\left[z^{-2}Y(z)+y(-2)+y(-1)z^{-1}\right]=X(z) \] 代入数据: \[ (1+3z^{-1}+2z^{-2})Y(z)+4=\frac{z} {z-2} \] 则: \[ \begin{aligned} Y(z)&=\frac {-4} {1+3z^{-1}+2z^{-2} }+\frac{1} {1+3z^{-1}+2z^{-2} }\frac{z} {z-2}\\\\ &=\frac{-4z^2} {z^2+3z+2}+\frac{z^2} {z^2+3z+2}\frac{z} {z-2} \end{aligned} \] 其中第一项代表零状态响应,第二项代表零输入响应。有: \[ Y_{zi}(z)=\frac{4z} {z+1}+\frac{-8z} {z+2} \]
\[ Y_{zs}(z)=\frac{-\frac 13 z} {z+1}+\frac{z} {z+2}+\frac{\frac 13 z} {z-2} \]
则: \[ y_{zi}(n)=4(-1)^n-8(-2)^n\\\\ y_{zs}(n)=-\frac 13 (-1)^n+(-2)^n+\frac 13 (2)^n \] (\(n\geq 0\))
离散系统传递函数
就是单位样值响应(零状态)\(h(n)\)的\(Z\)变换\(H(z)\),一般有如下形式:
\[ H(z)=\frac{\sum_{r=0}^M b_rz^{-r} } {\sum_{k=0}^N a_kz^{-k} }=G\frac{\prod _{r=1}^M (1-o_rz^{-1})} {\prod_{k=0}^N (1-p_kz^{-1})} \]
其中\(o\)就是零点,\(p\)就是极点。对于因果序列而言,极点分布和\(h(n)\)大致时域形状的关系如下:
| \(H(z)\)极点位置 | \(h(n)\)时域形状 |
|---|---|
| 单位圆内实数 | 指数衰减序列 |
| 单位圆内共轭复数 | 衰减的正弦序列 |
| 单位圆外实数 | 指数增长序列 |
| 单位圆外共轭复数 | 增长的正弦序列 |
| 单位圆上实数 | 常序列(一阶)或逐渐增大 |
| 单位圆上共轭复数 | 幅度为常数或逐渐增大的正弦序列 |
由此可以看出极点分布和系统稳定性的关系。另外,这个表也可以由\(s-z\)平面变换得出。
至于因果性,那就更简单了。只要系统函数的极点分布在\(Z\)平面内的一个半径有限的圆内就行,即保证收敛域为 \[ |z|>R \]
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
