关于傅里叶变换的那些事

所谓的变换，也就是信号的正交分解。如果两个函数的内积为\(0\)，我们称为这两个函数正交。那么对于任意信号\(f(t)\)，都可以写成一组正交函数系的和的形式（可以对比正交向量理解），这就是信号的正交分解。通过正交分解，可以对信号的特性有进一步的认识，也可以简化信号的分析和计算。

傅里叶级数

傅里叶级数是 周期信号 基于正交函数系\(\{e^{j\omega t}\}\)的正交分解。

三角函数形式的傅里叶级数

三角函数形式的傅里叶级数就是我们最熟悉的傅里叶级数。对于满足以下条件的函数\(f(t)\):

周期函数，周期为\(T_1\)，角频率为\(\omega_1=2\pi/T_1\)
间断点个数有限（可数）
极大极小值个数有限（可数）
绝对可积

有： \[ f(t)=a_{0}+\sum_{n=1}^{\infty}\left(a_{n} \cos n \omega_{1} t+b_{n} \sin n \omega_{1} t\right) \] 其中\(a_0\)叫直流分量，\(a_n\)叫\(n\)次谐波余弦分量，\(b_n\)叫\(n\)次谐波正弦分量。有计算公式： \[ a_0=\frac{1} {T_{1} } \int_{-\frac{T_{1} } {2} }^{\frac{T_{1} } {2} } f(t) \mathrm{d} t \]

\[ a_n=\frac{2} {T_{1} } \int_{-\frac{T_{1} } {2} }^{\frac{T_{1} } {2} } f(t) \cos n \omega_{1} t \mathrm{~d} t \]

\[ b_n=\frac{2} {T_{1} } \int_{-\frac{T_{1} } {2} }^{\frac{T_{1} } {2} } f(t) \sin n \omega_{1} t \mathrm{~d} t \]

当然，也可通过和差化积公式，转换成只有正弦或余弦分量的形式，此处不再赘述。

有： \[ a_n=a_{-n},-b_n=b_{-n} \]

指数形式傅里叶级数

因为： \[ \sin x=\frac{1} {2j}(e^{jx}-e^{-jx}) \]

\[ \cos x=\frac 12 (e^{jx}+e^{-jx}) \]

代入三角函数形式傅里叶级数中，就能得到指数形式傅里叶级数。这里给出部分关键步骤供参考。 \[ \begin{aligned} f(t)&=a_{0}+\sum_{n=1}^{\infty}\left(a_{n} \cos n \omega_{1} t+b_{n} \sin n \omega_{1} t\right)\\\\ &=a_{0}+\sum_{n=1}^{\infty}\left(\frac{a_{n}-j b_{n} } {2} e^{j n \omega_{1} t}+\frac{a_{n}+j b_{n} } {2} e^{-j n \omega_{1} t}\right)\\\\ &=a_{0}+\sum_{n=1}^{\infty} \frac{a_{n}-j b_{n} } {2} e^{j n \omega_{1} t}+\sum_{n=-\infty}^{-1} \frac{a_{n}-j b_{n} } {2} e^{j n \omega_{1} t} & a_n=a_{-n},-b_n=b_{-n}\\\\ &=\sum_{n=-\infty}^{\infty} F\left(n \omega_{1}\right) e^{j n \omega_{1} t} \end{aligned} \] 其中 \[ F\left(n \omega_{1}\right)=\begin{cases}a_{0}, & n=0 \\\\ \frac{a_{n}-j b_{n} } {2}, & n \neq 0\end{cases} \] 即 \[ F(n\omega_1)=\frac{1} {T_{1} } \int_{-\frac{T_{1} } {2} }^{\frac{T_{1} } {2} } f(t) e^{-j n \omega_{1} t} \mathrm{d} t \] 可以看出，\(F\left(n \omega_{1}\right)\)一般而言是一个复数。它的模长和幅角满足： \[ |F\left(n \omega_{1}\right)|=\frac 12 \sqrt{a_n^2+b_n^2} \]

\[ \tan \varphi_n=-\frac{b_n} {a_n} \]

函数的对称性和傅里叶级数

因为\(\cos\)是偶函数，\(\sin\)是奇函数，所以函数本身的奇偶对称性和傅里叶系数的奇偶对称性有关系。

信号	\(a_n\)	\(b_n\)	\(F(n\omega_1)\)	\(\varphi_n\)
奇函数	0	不为0	纯虚数	\(\pm \pi/2\)
偶函数	不为0	0	实数	\(\pm \pi\)
奇谐函数^[1]	只含奇次谐波	只含奇次谐波	同前	同前
偶谐函数	只含直流分量和偶次谐波	同前	同前	同前

我们需要注意到：一个“偶谐函数”，和一个周期为\(T_1/2\)的函数，实质上是一回事。

从傅里叶级数看傅里叶变换

傅里叶级数只能描述周期函数。但是我如果非得描述非周期函数，又会怎么样呢？我们来考虑一下怎么把非周期函数强行变成周期函数，其实只需要让周期\(T\)趋向于无穷大就好了。

对于 \[ F(n\omega_1)=\frac{1} {T_{1} } \int_{-\frac{T_{1} } {2} }^{\frac{T_{1} } {2} } f(t) e^{-j n \omega_{1} t} \mathrm{d} t \] 让\(T\)趋向于无穷大，则\(\omega\)趋向于无穷小。因为函数满足绝对可积条件，所以右边是一个有限值比无穷大，趋向于0。而左边因为\(\omega\)趋向于无穷小，取值点趋向于连续。有没有发现，这个过程有一点点像随机变量从连续型变成离散型时，分布列的变化情况（一方面，取值趋向于无穷小；另一方面，自变量趋向于连续）。于是，类似于“概率论”的知识，我们也可以定义“频谱密度函数”，让\(n\omega_1\to\omega\)，有 \[ F(\omega)=\int_{-\infty}^\infty f(t)e^{-j\omega t}\mathrm{d}t \] 这就是我们常说的傅里叶变换。

傅里叶变换

傅里叶变换的定义式

\[ F(\omega)=\int_{-\infty}^\infty f(t)e^{-j\omega t}\mathrm{d}t \]

基本信号及其傅里叶变换

矩形脉冲信号（门信号）

即： \[ G_N(t)=\begin{cases} 1 & |t|<N\\\\ 0 & |t|>N \end{cases} \] 有： \[ \mathscr{F}[G_N(t)]=2N\mathrm{Sa}(\omega N) \]
单边指数信号 \[ f_1(t)=\begin{cases} e^{-at} & t\geq 0\\\\ 0 & \text{others} \end{cases} \] 则 \[ \mathscr{F}[f_1(t)]=\frac {1} {a+j\omega} \] 类似地， \[ f_2(t)=\begin{cases} 0 & t\geq 0\\\\ e^{bt} & t<0 \end{cases} \] 则 \[ \mathscr{F}[f_2(t)]=\frac 1{b-j\omega} \]
“偶”双边指数信号

把前面两个单边指数信号加起来就行了。 \[ f(t)=e^{-a|t|} \] 则 \[ \mathscr{F}\left[e^{-a|t|}\right]=\frac{2a} {a^2+\omega^2} \]
符号函数 \[ \text{sgn}(t)=\begin{cases} 1 & t>0\\\\ 0 & t=0\\\\ -1 & t<0 \end{cases} \] 为求符号函数的傅里叶变换，先求“奇双边指数函数”的傅里叶变换，然后让指数系数趋向于0即可。

奇双边指数函数，即 \[ f(t)=\begin{cases} e^{-at} &t>0\\\\ -e^{-at} & t<0 \end{cases} \]

\[ \mathscr{F}[f(t)]=\frac{-2j\omega} {a^2+\omega^2} \]

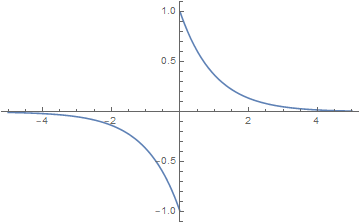
当\(a\to0\)时，这个函数就趋向于\(\text{sgn}(t)\)。如图是\(a=0.01\)的图像：

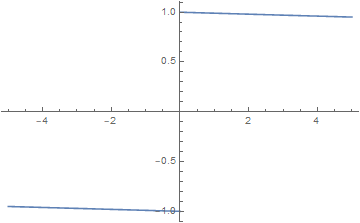
则有： \[ \mathscr{F}[\text{sgn}(t)]=\frac 2{j\omega} \]
冲激信号 \[ \mathscr{F}[\delta(t)]=1 \]
阶跃信号 \[ \mathscr{F}[u(t)]=\pi \delta(\omega)+\frac 1{j\omega} \] 这个结果可以通过符号函数平移得到。

傅里叶变换的性质

如果有： \[ \mathscr F[f(t)]=F(\omega) \] 则有：

基于定义的性质

对称性 \[ \mathscr F[F(t)]=2\pi f(-\omega) \]
奇虚偶实性
- \(|F(\omega)|\)是偶函数
- \(\varphi(\omega)\)是奇函数
- 如果\(f(t)\)是实偶函数，则\(F(\omega)\)是实偶函数
- 如果\(f(t)\)是实奇函数，则\(F(\omega)\)是虚奇函数

基于时间运算的性质

反褶性质 \[ \mathscr F[f(-t)]=F(-\omega)=F^*(\omega) \]
时移性质 \[ \mathscr F[f(t-t_0)]=F(\omega)e^{-j\omega t_0} \] 可以说：时移不改变幅频特性，而改变相频特性。
压扩性质 \[ \mathscr F[f(at)]=\frac 1{|a|}F\left(\frac \omega a\right) \] 对于频域带限信号，时域的压缩和扩展，会导致频谱范围的增大和减小，频率分量的减少和增加。
时域综合性质 \[ \mathscr F[f(at+b)]=\frac 1{|a|}F\left(\frac \omega a\right)e^{j\omega\frac ba} \]
线性
时域微分性质 \[ \mathscr F[f'(t)]=j\omega F(\omega) \] 进一步： \[ \mathscr F[f^{(n)}(t)]=(j\omega)^nF(\omega) \] 因为函数加上任意常数后，微分都相同。在运用这个性质时，要把信号的直流分量提取出来单独处理。例如：尝试利用时域微分性质和线性性质分别由\(\text{sgn}(t)\)函数的傅里叶变换计算\(u(t)\)的傅里叶变换，并比较结果。
时域积分性质 \[ \mathscr F\left[\int_{-\infty}^t f(\tau)\mathrm d\tau\right]=\frac {F(\omega)} {j\omega}+\pi F(0)\delta(\omega) \]

基于频域运算的性质

频移性质 \[ \mathscr F[f(t)e^{j\omega_0 t}]=F(\omega-\omega_0) \]
频域微分-时域线性加权性质 \[ \mathscr F[t^nf(t)]=j^n \frac{\mathrm d^nF(\omega)} {\mathrm d \omega^n} \]

卷积性质

时域卷积 \[ \mathscr F[f_1(t)\bigotimes f_2(t)]=F_1(\omega)F_2(\omega) \]
频域卷积 \[ \mathscr F[f_1(t)f_2(t)]=\frac 1{2\pi}F_1(\omega)\bigotimes F_2(\omega) \]

由变换的性质计算常用信号的傅里叶变换

直流信号\(E\)

由 \[ \mathscr F[\delta(t)]=1 \] 因对称性，有： \[ \mathscr F[1]=2\pi \delta(\omega) \] 因线性，有： \[ \mathscr F[E]=2\pi E\delta(\omega) \]
\(f(t)=1/t\)

由 \[ \mathscr F[\text{sgn} (t)]=\frac 2{j\omega} \] 因对称性，有： \[ \mathscr F\left[\frac 2{jt}\right]=2\pi\text{sgn}(-\omega) \] 因线性，有： \[ \mathscr F\left[\frac 1 t\right]=-j\pi\text{sgn}(\omega) \]
正余弦信号

由 \[ \mathscr F[1]=2\pi\delta(\omega) \] 因频移性质，有： \[ \mathscr F[e^{j\omega_0t}]=2\pi\delta(\omega-\omega_0)\\\\ \mathscr F[e^{-j\omega_0t}]=2\pi\delta(\omega+\omega_0)\\\\ \] 因三角函数分解公式： \[ \sin \omega_0t=\frac{1} {2j}(e^{j\omega_0t}-e^{-j\omega_0t})\\\\ \cos \omega_0t=\frac 12 (e^{j\omega_0t}+e^{-j\omega_0t}) \] 有： \[ \mathscr F[\sin(\omega_0 t)]=-j\pi [\delta(\omega-\omega_0)-\delta(\omega+\omega_0)]\\\\ \mathscr F [\cos(\omega_0 t)]=\pi[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)] \]
三角脉冲信号

定义三角脉冲信号\(T_\tau(t)\)为形如下面的信号，计算傅里叶变换。

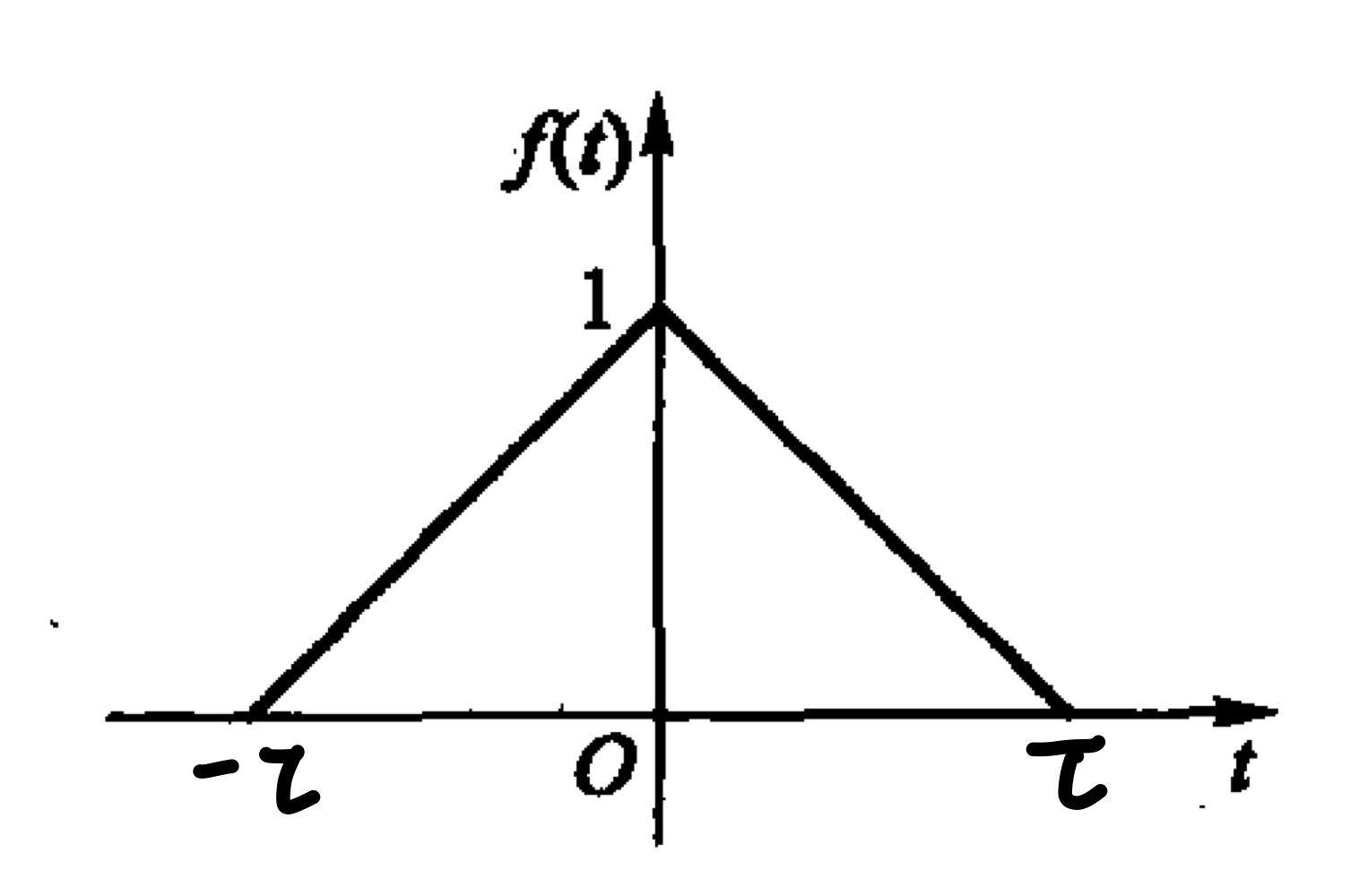
由 \[ \mathscr F[G_N(t)]=2N\text{Sa}(N\omega) \] 则三角脉冲信号\(T_\tau(t)\)是门信号的卷积，具体地： \[ T_\tau(t)=\sqrt{\frac 1\tau}G_{\frac \tau2}(t)\bigotimes\sqrt{\frac 1\tau}G_{\frac \tau2}(t) \] 由于 \[ \mathscr F\left[\sqrt{\frac 1\tau}G_{\frac \tau2}(t)\right]=\sqrt{\tau}\text{Sa}\left(\frac \tau2\omega\right) \] 和卷积性质，有： \[ \mathscr F[T_\tau(t)]=\tau\text{Sa}^2\left(\frac \tau2 \omega\right) \]

现将常用信号的傅里叶变换归纳如下：

\(f(t)\)	\(F(\omega)\)
\(\delta(t)\)	\(1\)
\(\delta (t-t_0)\)	\(e^{-j\omega t_0}\)
\(1\)	\(2\pi\delta(\omega)\)
\(e^{j\omega_0t}\)	\(2\pi\delta(\omega-\omega_0)\)
\(u(t)\)	\(\pi\delta(\omega)-\frac 1{j\omega}\)
\(sgn(t)\)	\(\frac 2{j\omega}\)
\(\cos(\omega_0t)\)	\(\pi[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)]\)
\(\sin(\omega_0t)\)	\(-j\pi [\delta(\omega-\omega_0)-\delta(\omega+\omega_0)]\)
\(e^{-a\\|t\\|}\)	\(\frac{2a} {a^2+\omega^2}\)
\(G_N(t)\)	\(2NSa(N\omega)\)
\(T_\tau(t)\)	\(\tau\text{Sa}^2\left(\frac \tau2 \omega\right)\)
\(e^{-at}u(t)\)	\(\frac{1} {j\omega+a}\)
\(1/t\)	\(-j\pi\text{sgn}(\omega)\)

这里提出一个趣味问题：

【例】：是否存在一个时域、频域都有限的信号？

【解】：不存在。如果时域有限，则信号可以表示为： \[ f(t)=f(t)G_N(t-t_0) \] 而\(G_N(t)\)的傅里叶变换的频带是无限的。卷积之后，频带也是无限长的。频域有限情况同理可知。

周期信号的傅里叶变换

在之前，我们研究的是周期信号的傅里叶级数，和非周期信号的傅里叶变换。现在为了把它们都纳入傅里叶分析的框架中，我们要讨论周期信号的傅里叶变换。

我们都知道，周期信号的傅里叶系数\(F(n\omega)\)叫“频谱函数”，而非周期信号的傅里叶变换\(F(\omega)\)叫“频谱密度函数”。那么如果我们非要用频谱密度函数来表示频谱函数，那么结果应该是出现在其角频率各次谐波处的冲激函数。（请联想概率论中，如果我们非要用“概率密度函数”来表示离散分布的“分布函数”，那么会出现什么现象？）

周期函数的傅里叶系数和它一个周期内函数的傅里叶变换的关系为：

\[ F(n\omega_1)=\left.\frac 1{T_1}F_1(\omega)\right|_{\omega=n\omega_1} \]

对于周期函数的傅里叶级数

\[ f(t)=\sum_{n=-\infty}^{\infty} F\left(n \omega_{1}\right) e^{j n \omega_{1} t} \]

作傅里叶变换：

\[ \mathscr F\left[\sum_{n=-\infty}^{\infty} F\left(n \omega_{1}\right) e^{j n \omega_{1} t}\right]=\sum_{n=-\infty}^{\infty}F(n\omega_1)\mathscr F[e^{jn\omega_1 t}] \]

由于频移性质：

\[ \mathscr F [e^{jn\omega_1 t}]=2\pi\delta(\omega-n\omega_1) \]

故：

\[ \mathscr F[f(t)]=\mathscr F\left[\sum_{n=-\infty}^{\infty} F\left(n \omega_{1}\right) e^{j n \omega_{1} t}\right]=2\pi\sum_{n=-\infty}^{\infty}F(n\omega_1)\delta(\omega-n\omega_1) \]

这就是一般周期信号的傅里叶变换。

典型周期信号的傅里叶变换

正余弦信号

正余弦信号的傅里叶变换我们之前已经求过了。现在我们可以从一个新的视角来考虑这个问题。对于余弦信号而言，有：

\[ \cos(\omega_1 t)=\frac 12(e^{j\omega_1 t}+e^{-j\omega_1t}) \]

则其傅里叶级数的系数为：

\[ F(n\omega_1)|_{n=\pm 1}=\frac 12 \]

则其傅里叶变换为：

\[ \mathscr F[\cos(\omega_1 t)]=\pi[\delta(\omega-\omega_1)+\delta(\omega+\omega_1)] \]
周期冲激信号

周期冲激信号经常被用来采样，所以也算是一个常用的信号。我们来看一下它的傅里叶变换。

周期冲激信号的定义是：

\[ \delta_{T_1}(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT_1) \]

其傅里叶系数为：

\[ F(n\omega_1)=\left.\frac 1{T_1}F_1(\omega)\right|_{\omega=n\omega_1}=\frac1{T_1} \]

则其傅里叶变换为：

\[ \mathscr F[\delta_{T_1}(t)]=\frac {2\pi} {T_1}\sum_{n=-\infty}^\infty \delta(\omega-n\omega_1)=\omega_1\sum_{n=-\infty}^\infty \delta(\omega-n\omega_1) \]

可以看出：周期冲激信号的傅里叶变换也是周期冲激信号。
周期矩形脉冲信号

周期矩形脉冲信号有两个参数：周期\(T_1\)，脉宽\(\tau\)，即：

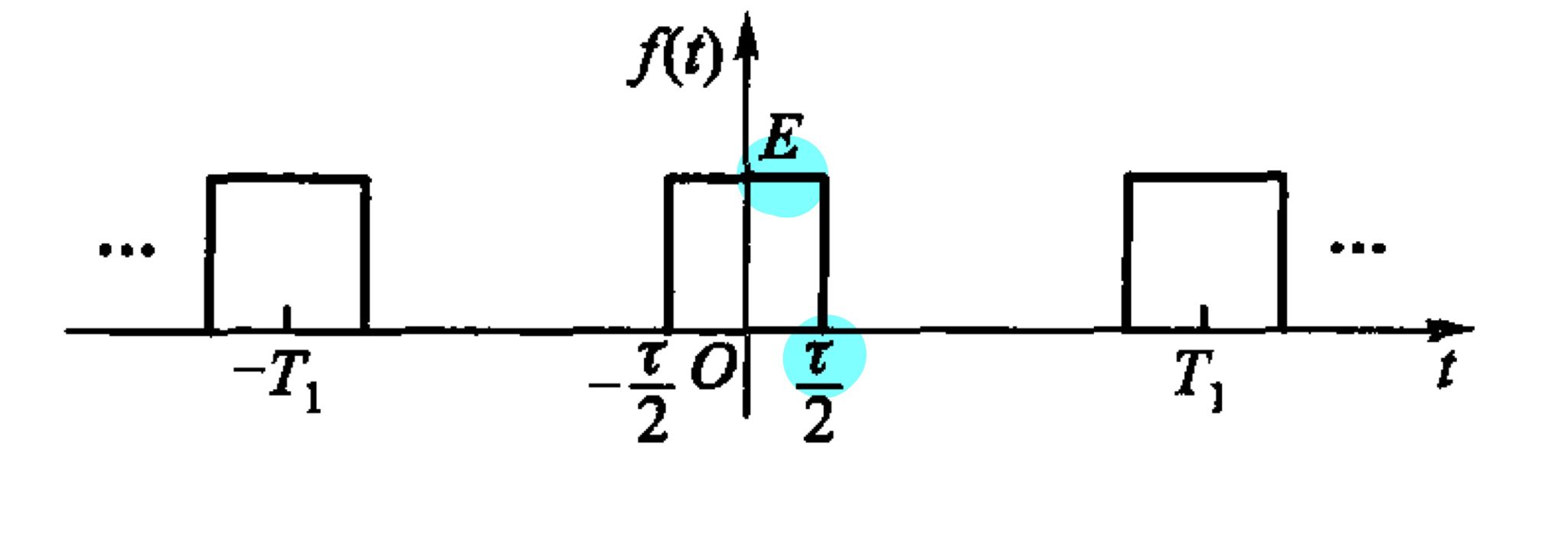
记作：\(G_{T_1,\tau}(t)\)，图中\(E=1\).

在一个周期中，其傅里叶变换为：

\[ \mathscr F[G_{0,\tau}(t)]=\tau\text{Sa}\left(\frac{\omega\tau} {2}\right) \]

则周期矩形脉冲的傅里叶系数为

\[ F(n\omega_1)=\frac{\tau} {T_1}\text{Sa}\left(\frac{n\omega_1\tau} {2}\right) \]

故周期矩形脉冲的傅里叶变换为

\[ \tau\omega_1\sum_{n=-\infty}^{\infty}\text{Sa}\left(\frac{n\omega_1\tau} {2}\right)\delta(\omega-n\omega_1) \]

抽样

一个基本的抽样过程等效于以下的模型：

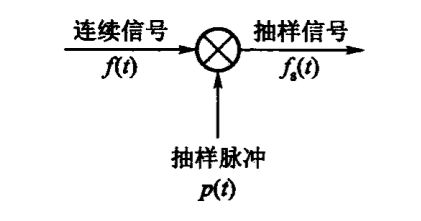
这里的"\(\bigotimes\)"是乘法的意思。即有：

\[ f_s(t)=f(t)p(t) \]

这里的\(p(t)\)就是脉冲信号，比如说周期冲激信号，周期矩形脉冲信号等等。

利用傅里叶变换的卷积定理，有（这里要熟练掌握冲激函数的卷积性质）：

\[ \mathscr F[f_s(t)]=\frac 1{T_s}\sum_{n=-\infty}^{\infty}P_0(n\omega_s)F(\omega-n\omega_s) \]

也就是说，抽样信号的频谱是连续信号频谱以\(\omega_s\)为周期的周期延拓，并收到脉冲信号频谱\(P_0(n\omega_s)\)和脉冲信号周期\(T_s\)的加权。

于是，我们发现，如果要求不发生频域混叠，那么原始连续信号必须在频域是带限信号。但是这实际上是不可能存在的。但是信号的主要频域往往确实是有限的，其它部分的分量可以忽略不计，为此我们可以定义\(-3\text{dB}\)带宽，零点带宽等带宽（记作\(\omega_m\)），把信号近似为一个频域带限信号。

那么，一个带限信号\(f(t)\),如果其频谱存在在频域区间\([-\omega_m,\omega_m]\)，则可用抽样值唯一表示\(f(t)\),抽样值的间隔不能大于\(T_s=\frac{1} {2f_m}\),其中\(f_m=\frac{\omega_m} {2\pi}\)，否则会发生频域混叠，这就是奈奎斯特采样定理。我们把\(f_s=2f_m\)称作“奈奎斯特频率”，这是不发生频域混叠的最小抽样频率。

为了从抽样信号中恢复出原始信号，对理想冲激抽样，我们用一个截止频率为\(\omega_c\)，幅度增益为\(T_s\)的零延时低通滤波器即可，其中\(\omega_c\)满足\(\omega_c\in[\omega_m,\omega_s-\omega_m]\).对于理想矩形脉冲抽样，滤波器的幅度增益应为\(T_s/(E\tau)\)

连续系统实频域分析

所谓的连续系统实频域分析，也就是利用傅里叶变换来分析连续系统。在本节，将首先介绍系统传递函数的概念，再介绍一类比较理想的系统：无失真系统，然后分析一类具体的系统：低通滤波器。

系统频率响应

定义系统单位冲激响应\(h(t)\)的傅里叶变换为系统频率响应。即：

\[ H(\omega)=\int_{-\infty}^\infty h(t)e^{-j\omega t}\mathrm d t \]

如果系统的激励为\(e(t)\),激励的傅里叶变换为\(E(\omega)\)，那么对系统的响应的傅里叶变换，有：

\[ R(\omega)=E(\omega)\cdot H(\omega) \]

如果系统输入的是复指数信号\(e^{j\omega_0 t}\)，那么有：

\[ R=2\pi\delta(\omega-\omega_0)H(\omega) \]

则有：

\[ r(t)=\frac 1{2\pi}\int_{-\infty}^{\infty}2\pi\delta(\omega-\omega_0)H(\omega)e^{j\omega t}\mathrm d t=e^{j\omega_0t}H(\omega_0) \]

这说明：系统对不同频率的正弦信号的幅度和相位加权不相同；不同的系统对相同频率的正弦信号的幅度和相位的加权也不相同。

对于频率响应\(H(\omega)\)，称\(|H(\omega)|\)为系统的幅频响应，而\(\varphi(\omega)\)为系统的相频响应。

如果系统用微分方程

\[ C_0r^{(n)}(t)+C_1r^{(n-1)}(t)+\cdots+C_nr(t)=E_0e^{(m)}(t)+E_1e^{(m-1)}(t)+\cdots+E_me(t) \]

可以直接写出其频率响应：

\[ H(\omega)=\frac{\sum_{i=0}^nC_i(j\omega)^{n-i} } {\sum_{j=1}^m E_{j}(j\omega)^{m-j} } \]

在已知频率响应和激励，求系统响应时，一般有两种思路。其一是系统激励以傅里叶级数形式给出，这时只需要针对每个谐波分量计算对应的幅频响应和相频响应，然后把响应作用于激励即可。另一种思路是先求出激励的傅里叶变换，然后用图像和系统频率响应相乘，得到响应的傅里叶变换，最后得到结果。

无失真系统

输出响应能再现系统的输入，只有出现时刻和幅度不同，即没有改变输入波形的形状，这种系统叫做无失真系统。那么把冲激信号输入系统，就可以得到无失真系统的频响：

\[ H(\omega)=ke^{-j\omega t_0} \]

则其幅频，相频特性如下：

\[ |H(\omega)|=k\\\\ \varphi(\omega)=-\omega t_0 \]

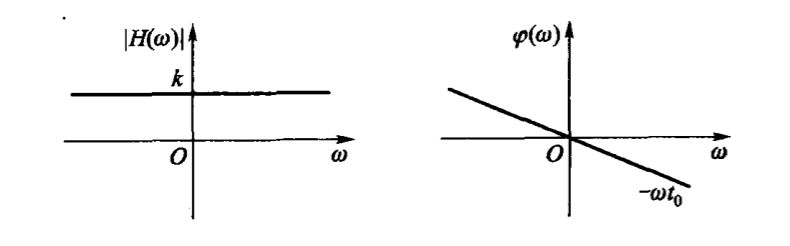
相频特性是一条直线的含义是：相频特性表示了系统的延时，对信号的所有频率分量，应该有相同的延时，即相位附加值相同。例如输入\(E_1\sin(\omega_1t)\)，那么理应得到输出\(E_1\sin\left[\omega(t+\varphi(\omega))\right]=E_1\sin\left[\omega(t+\frac{\varphi(\omega)} {\omega})\right]\)，于是，为了对不同的频率分量得到相同的附加相移，就需要：

\[ \forall \omega_1,\omega_2,\frac{\varphi(\omega_1)} {\omega_1}=\frac{\varphi(\omega_2)} {\omega_2} \]

低通滤波器

理想滤波器是在特定频段范围内的无失真传输系统。这里之所以只讨论低通滤波器，是其它滤波器可以由低通滤波器转换而来。具体如何转换，我们后面再说。

理想低通滤波器的频响特性如下：

\[ H(\omega)= \begin{cases}e^{-j \omega t_{0} } & |\omega|<\omega_{c} \\\\ 0 & |\omega| \geq \omega_{c}\end{cases} \]

注意，切不可以以为理想低通滤波器的频响函数是频域门函数，因为还要考虑附加相移（时域延迟）。有：

\[ |{H}(\omega)|= \begin{cases}1 & |\omega|<\omega_{c} \\\\ 0 & |\omega| \geq \omega_{c}\end{cases} \]

\[ \varphi(\omega)= \begin{cases}-\omega t_{0} & |\omega|<\omega_{c} \\\\ 0 & |\omega| \geq \omega_{c}\end{cases} \]

对频响函数作傅里叶逆变换，可得单位冲激响应：

\[ h(t) =\frac{\omega_{c} } {\pi} \cdot \text{Sa}\left[\omega_{c}\left(t-t_{0}\right)\right] \]

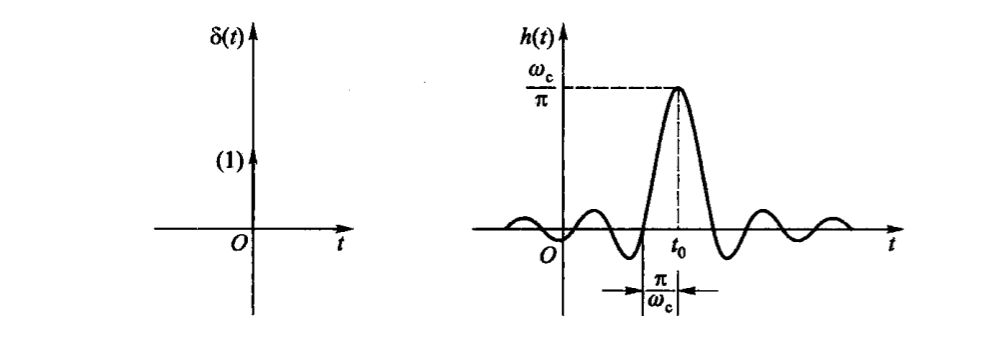
其它滤波器

高通滤波器

无失真全通系统-低通滤波器=高通滤波器。因而，有：

\[ H_{h}(\omega)=e^{-\mathrm{j} \omega t_{0} }\left[1-u\left(\omega+\omega_{c}\right)+u\left(\omega-\omega_{c}\right)\right] \]

\[ h_{h}(t)=\delta\left(t-t_{0}\right)-h_{l}(t)=\delta\left(t-t_{0}\right)-\frac{\omega_{c} } {\pi} \cdot \mathrm{Sa}\left[\omega_{c}\left(t-t_{0}\right)\right] \]
带通滤波器

带通滤波器可以由理想低通滤波器频响向两侧搬移，再对相频特性进行修正得到。

\[ H_{b}(\omega)=e^{-\mathrm{j} \omega_{0} }\left[\left(u\left(\omega+\omega_{h}\right)-u\left(\omega+\omega_{l}\right)\right)+\left(u\left(\omega-\omega_{l}\right)-u\left(\omega-\omega_{h}\right)\right)\right] \]

\[ h_{b}(t)=\frac{2 \omega_{c} } {\pi} \cdot \operatorname{Sa}\left[\omega_{c}\left(t-t_{0}\right)\right] \cos \left[\omega_{0}\left(t-t_{0}\right)\right] \]

其中

\[ \omega_{c}=\frac{\omega_{h}-\omega_{l} } {2}, \omega_{0}=\frac{\omega_{h}+\omega_{l} } {2} \]

系统的因果性

我们都知道，\(LTI\)系统因果的充要条件是：

\[ h(t)=h(t)u(t) \]

现在我们从频域考虑这个问题。

佩里维纳准则

一个幅频响应绝对可积的系统物理可实现的必要条件是：

\[ \int_{-\infty}^{\infty}\frac{|\ \ln|H(\omega)|\ |} {1+\omega^2}\mathrm d\omega<\infty \]

从直观角度考虑，佩里维纳准则要求系统的幅频响应不能衰减得太快。特别的，如果幅频响应在某个连续频带上为\(0\)，那么系统就不可实现。

希尔伯特变换

接下来从时域入手，讨论判断系统因果性的充要条件。

从用卷积性质计算\(h(t)u(t)\)的傅里叶变换入手，设\(H(\omega)=R(\omega)+jX(\omega)\)，那么\(R,X\)构成一希尔伯特变换对。所谓的希尔伯特变换是指：

\[ \hat{x}(t)=\mathscr H[x(t)]=x(t)\bigotimes\frac1{\pi t} \]

把卷积展开，有：

\[ \begin{aligned} \hat{x}(t) &=\frac{1} {\pi} \int_{-\infty}^{\infty} x(\tau) \frac{1} {t-\tau} d \tau \\\\ &=-\frac{1} {\pi} \int_{-\infty}^{\infty} x(t+\tau) \frac{1} {\tau} d \tau \\\\ &=\frac{1} {\pi} \int_{-\infty}^{\infty} x(t-\tau) \frac{1} {\tau} d \tau \end{aligned} \]

对一个系统作希尔伯特变换，实质上是将其经过一个\(\pi/2\)相移器（注意：这里不是时移）。

希尔伯特变换将在《随机过程理论》中再次详细说明，这里只提两个重要性质：

\[ \mathscr F[\hat{x}(t)]=-j\mathscr F[x(t)]sgn(\omega) \]
\[ \mathscr H[\hat{x}(t)]=-x(t) \]

则系统因果的充要条件是：频响函数\(H(\omega)\)的实部和虚部是一对希尔伯特变换对。