信号与系统实验3:离散时间系统特性分析
这是信号与系统的实验报告。我信号与系统总共就扣了几分,也不知道是期末扣的,还是实验扣的。即使全是实验扣的,这实验也算做的挺好的。于是把报告发出来给大家参考。 这是第三个实验,离散时间系统特性分析
实验目的
深入理解单位样值相应,离散系统的频率响应的概念;
掌握通过计算机进行求得离散系统的单位样值相应,以及离散系统的频率响应的方法。
实验原理
对于离散系统的单位样值而言,在实际处理过程中,不可能选取无穷多项的取值。往往是选取有限项的取值,当然这里会产生一个截尾误差,但只要这个误差在相对小一个范围里,可以忽略不计。
另外,在一些实际的离散系统中,往往不是事先就能得到描述系统的差分方程的,而是通过得到系统的某些相应值,则此时系统的分析就需借助计算机的数值处理来进行,得到描述系统的某些特征,甚至进而得到描述系统的数学模型。
本实验首先给出描述系统的差分方程,通过迭代的方法求得系统的单位样值响应,进而求得该离散系统的频率响应。限于试验条件,虽然给出了系统方程,但处理的方法依然具有同样的实际意义。
具体的方法是:
1.在给定系统方程的条件下,选取激励信号为\(\delta(n)\),系统的起始状态为零状态,通过迭代法,求得系统的单位样值响应\(h(n)(n=0,1,\cdots,N)\)
2.利用公式 \[ H(e^{j\Omega})=\sum_{n=0}^Nh(n)e^{-j\Omega n},\Omega\in[0,2\pi] \] 计算系统的频率响应。
实验内容
求单位样值响应
已知系统: \[ y(n)-1.3y(n-1)-0.4y(n-2)=x(n-1) \] 求单位样值响应。
可以用迭代法求解,迭代公式为: \[ y(n)=x(n-1)+1.3y(n-1)+0.4y(n-2) \]
求系统幅频响应
利用公式 \[ H(e^{j\Omega})=\sum_{n=0}^Nh(n)e^{-j\Omega n},\Omega\in[0,2\pi] \] 计算系统的频率响应。
需要注意,计算出的\(H(e^{j\Omega})\)是一个复数,但是C语言对复数的支持并不是很好,因此我们可以分别计算实部和虚部。有:
\[ \Re\left[H(e^{j\Omega})\right]=\sum_{k=0}^{10}h(k)\cos(-\Omega k)\\\\ \Im\left[H(e^{j\Omega})\right]=\sum_{k=0}^{10}h(k)\sin(-\Omega k)\\\\ \text{Amp}=|H(e^{j\Omega})|=\sqrt{\Re ^2+\Im ^2}\\\\ \varphi=\arctan(\frac{\Re\left[H(e^{j\Omega})\right]}{\Im\left[H(e^{j\Omega})\right]}) \]
实验代码及其流程图
实验流程图如下:
实验代码如下:
1 | |
实验结果
系统单位样值响应
| \(n\) | \(\delta(n)\) | \(h(n)\) |
|---|---|---|
| 0 | 1 | 0.000000 |
| 1 | 0 | 1.000000 |
| 2 | 0 | 1.300000 |
| 3 | 0 | 1.290000 |
| 4 | 0 | 1.157000 |
| 5 | 0 | 0.988100 |
| 6 | 0 | 0.821730 |
| 7 | 0 | 0.673009 |
| 8 | 0 | 0.546220 |
| 9 | 0 | 0.440882 |
| 10 | 0 | 0.354659 |
响应-时间图如下
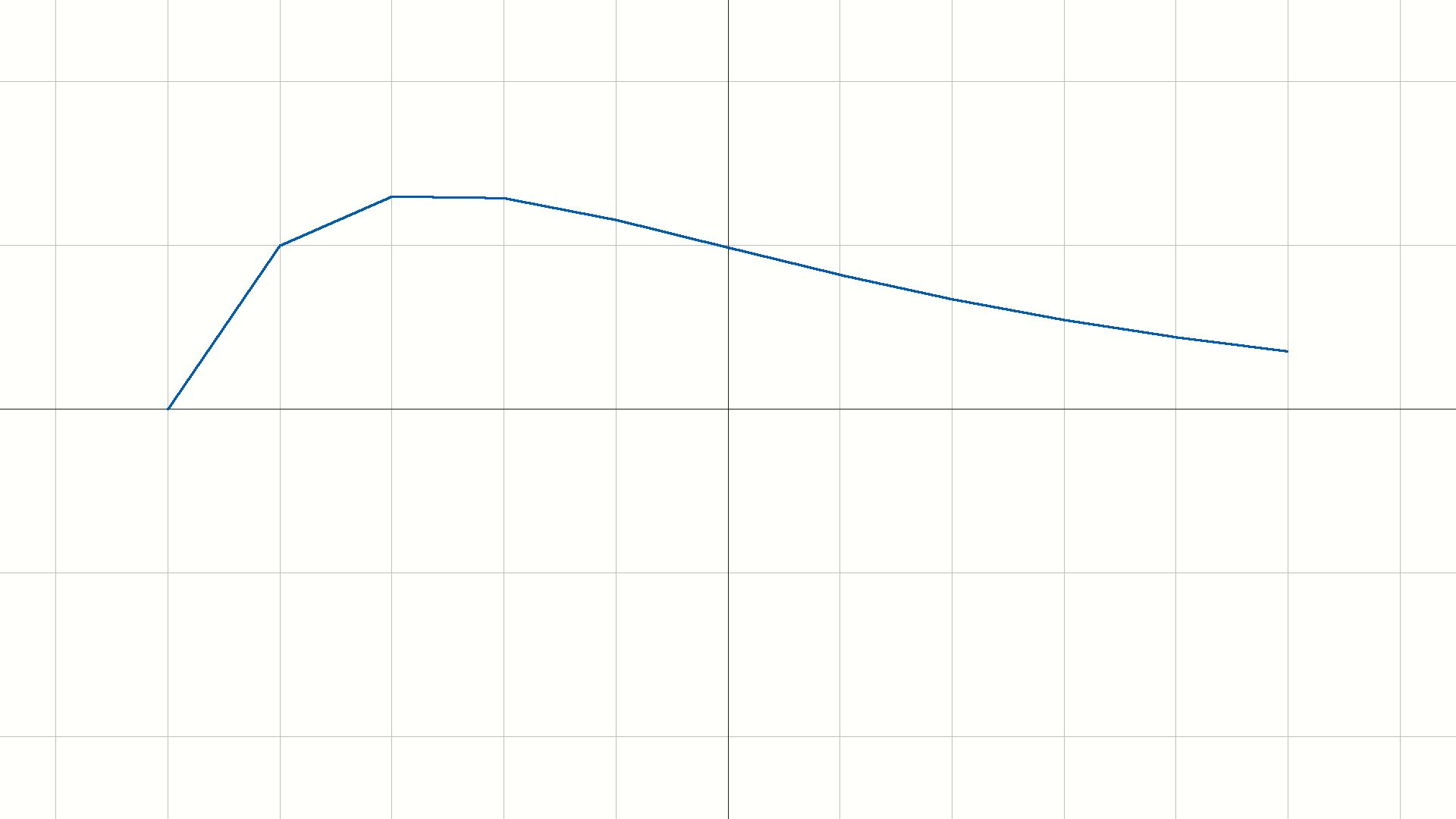
系统幅频和相频特性
| \(\Omega\) | \(\text{Amp}(\Omega)\) | \(\varphi(\Omega)\) |
|---|---|---|
| 0.0000 | 8.5716 | 0.0000 |
| 0.3142 | 6.1182 | -1.3645 |
| 0.6283 | 2.1370 | -2.1140 |
| 0.9425 | 1.7731 | -2.2523 |
| 1.2566 | 0.7426 | -2.7356 |
| 1.5708 | 0.9027 | -2.5992 |
| 1.8850 | 0.3754 | -3.0217 |
| 2.1991 | 0.6304 | -2.8331 |
| 2.5133 | 0.2467 | -3.1356 |
| 2.8274 | 0.5384 | -3.0404 |
| 3.1416 | 0.2124 | 3.1416 |
| 3.4558 | 0.5384 | 3.0404 |
| 3.7699 | 0.2467 | 3.1356 |
| 4.0841 | 0.6304 | 2.8331 |
| 4.3982 | 0.3754 | 3.0217 |
| 4.7124 | 0.9027 | 2.5992 |
| 5.0265 | 0.7426 | 2.7356 |
| 5.3407 | 1.7731 | 2.2523 |
| 5.6549 | 2.1370 | 2.1140 |
| 5.9690 | 6.1182 | 1.3645 |
| 6.2832 | 8.5716 | 0.0000 |
幅频曲线如下:
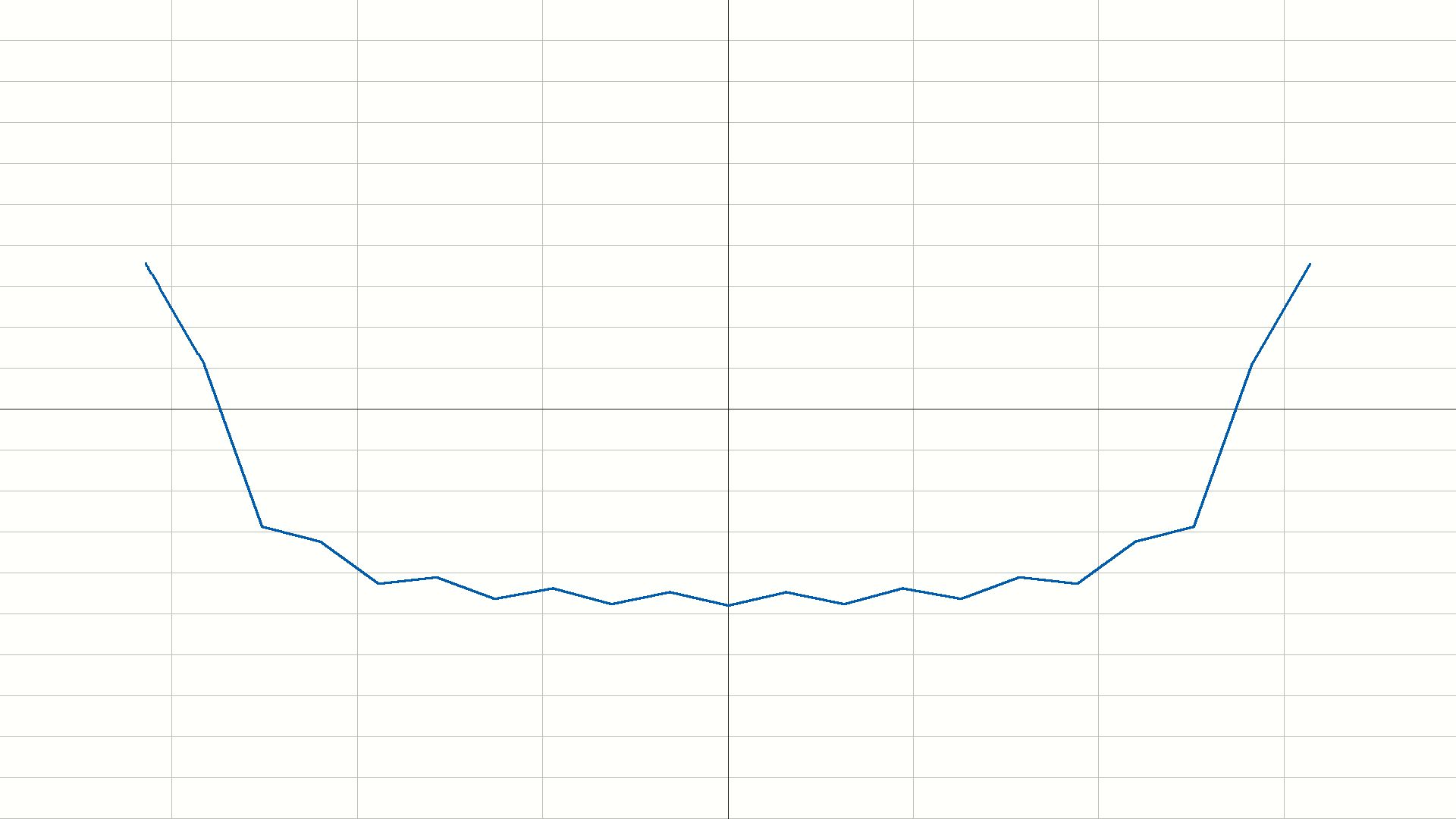
相频曲线如下:
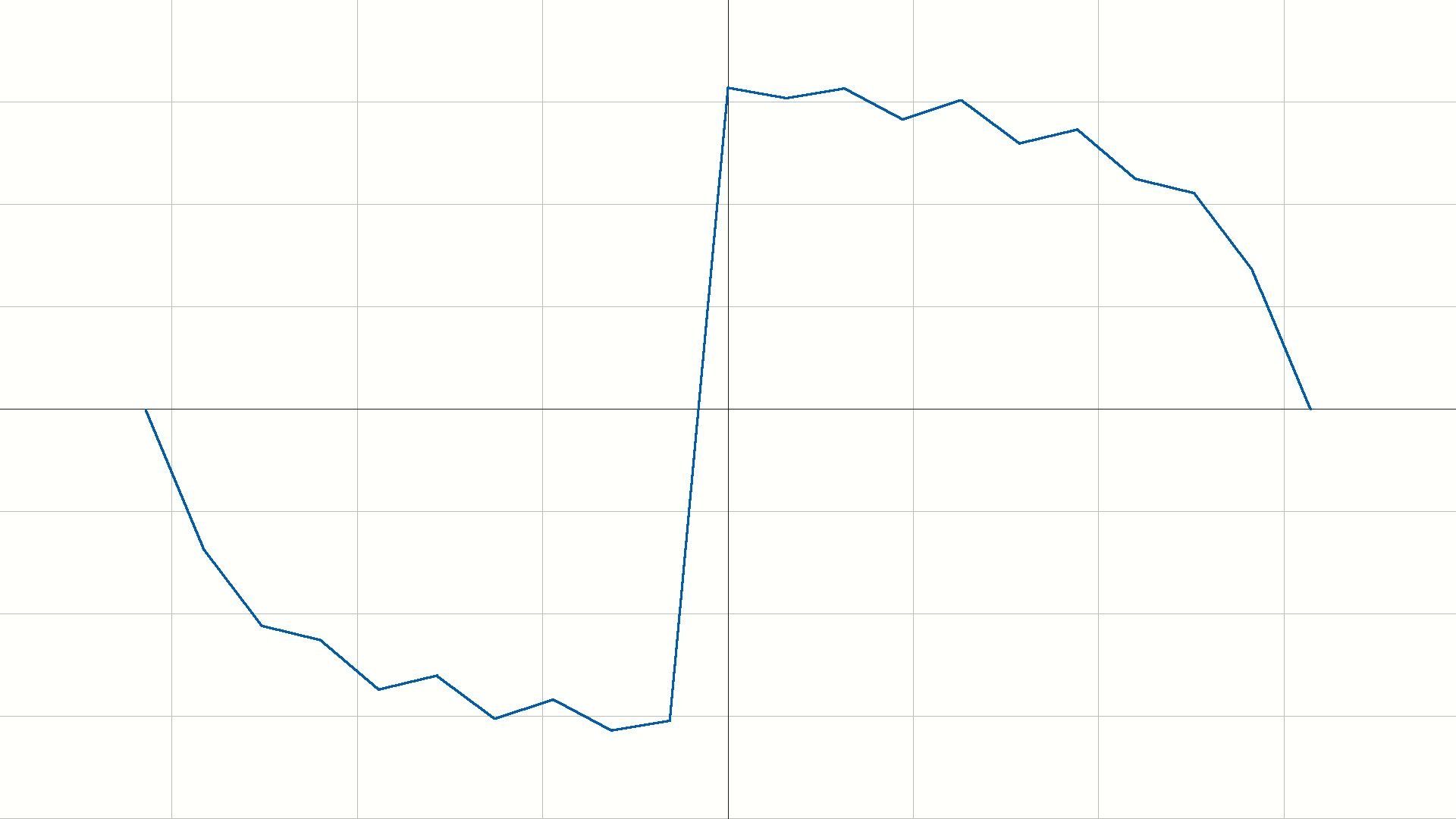
实验总结
\(0\)时对应的是低频,\(\pi\)时对应的是高频,通过幅频特性曲线可以看出,本系统是离散的低通滤波器。
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:

