信号与系统课程设计：频分复用系统设计
这是信号与系统的实验报告。我信号与系统总共就扣了几分，也不知道是期末扣的，还是实验扣的。即使全是实验扣的，这实验也算做的挺好的。于是把报告发出来给大家参考。 这是大作业，频分复用系统设计
实验目的
本次实验尝试设计一种频分复用系统，接收三个带限信号，通过选取不同的调制频率\(\omega_c\)，将所需传输的信号的频谱搬移到不同频段，在同一物理信道中传输多路信号。频分复用的原理框图如下：
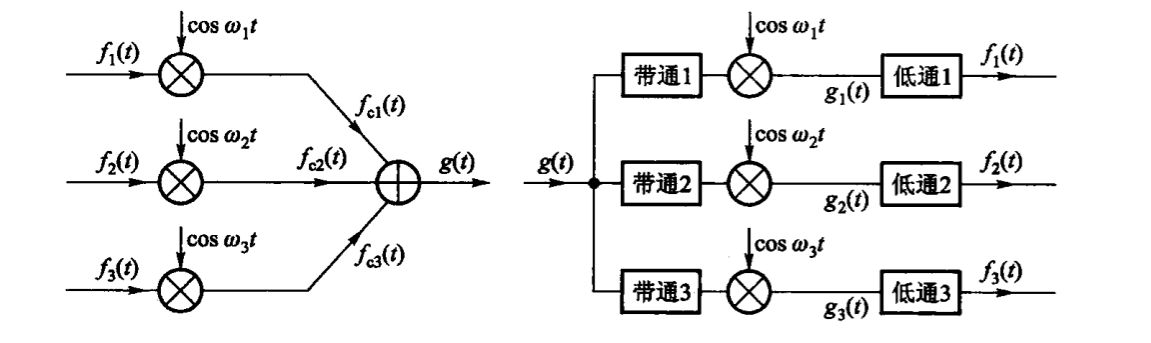
实验过程
读取信号
输入信号以列表的方式给出，表的形式如下：
| \(t\) | \(f_1(t)\) | \(f_2(t)\) | \(f_3(t)\) |
|---|---|---|---|
| -10 | -0.0498 | 0.0032 | 0.0031 |
| -9.9 | -0.0424 | 0.0023 | 0.0032 |
| -9.8 | -0.0344 | 0.0015 | 0.0031 |
| -9.7 | -0.0258 | 0.0008 | 0.003 |
| -9.6 | -0.0167 | 0.0004 | 0.0028 |
| -9.5 | -0.0073 | 0.0001 | 0.0025 |
| … | … | … | … |
| 9.8 | -0.0344 | 0.0015 | 0.0031 |
| 9.9 | -0.0424 | 0.0023 | 0.0032 |
读取数据相关的程序如下：
1 | |
其中tf结构体是为运算方便定义的结构，其中有两个double型量，即t和f，用来存储时间-信号表。
原始信号的波形如下：
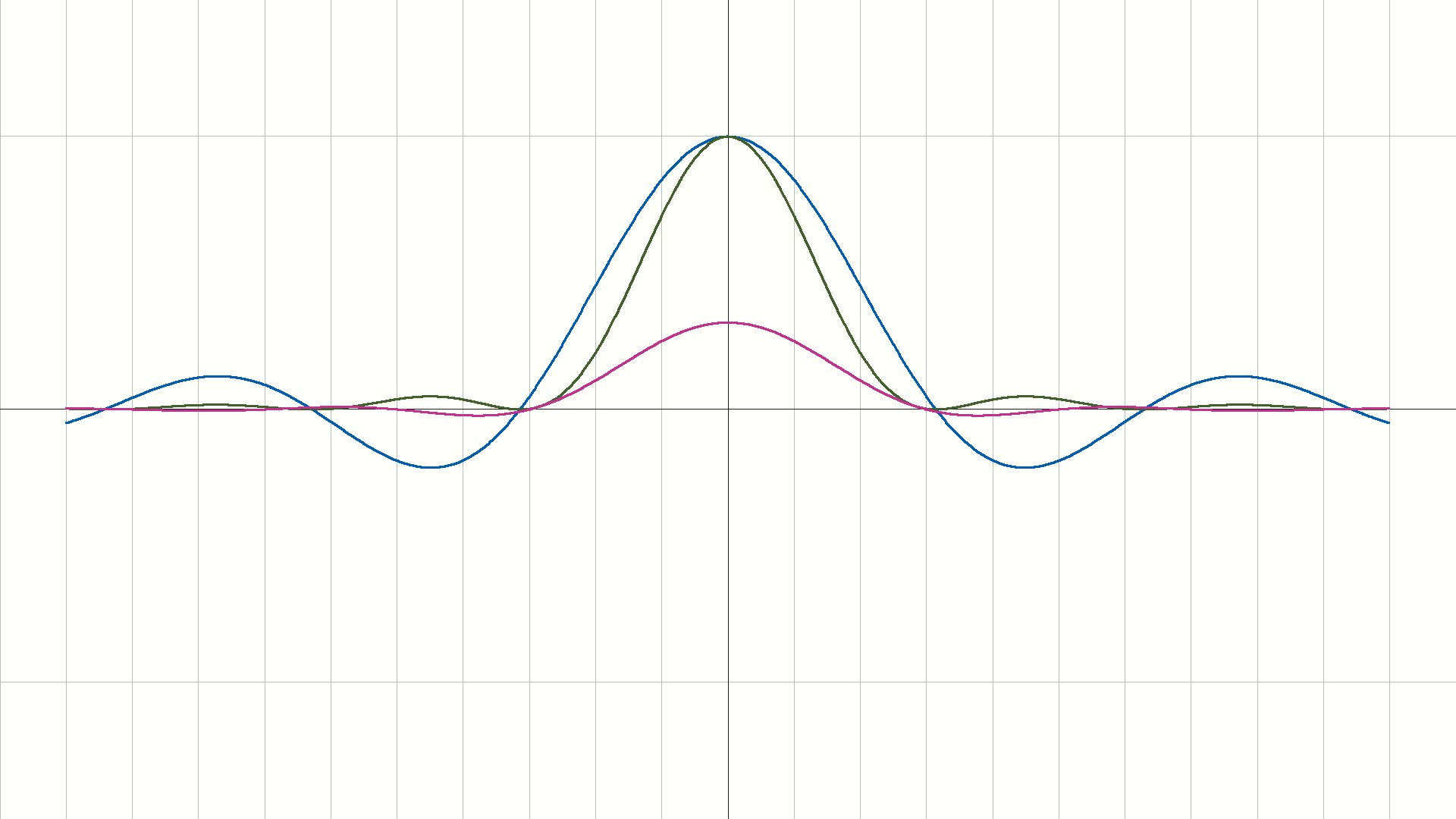
获取原始信号的频域图像，分析频域特征
对三个原始信号作傅里叶变换，并绘制频域图像：
1 | |
其中fourierTransform函数定义如下：
1 | |
绘制出的频域波形如下：
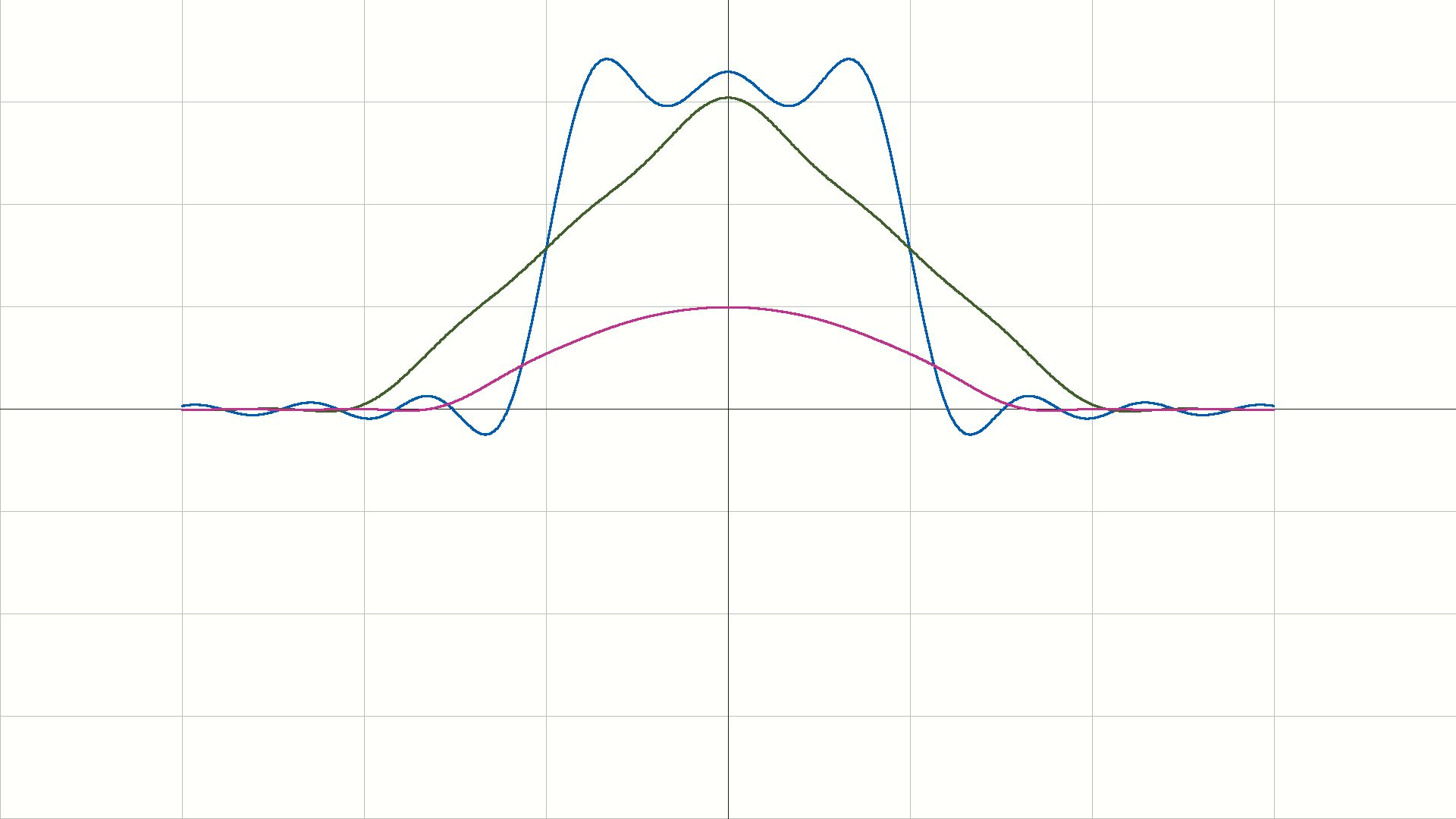
可以看出，输入的三个信号都是带限信号。有： \[ \omega_{m1}=1\\ \omega_{m2}=2\\ \omega_{m3}=\frac \pi 2 \] 因此，我们可以使用频分复用的方法把这三个信号合在一个信道中传输。
频域搬移和信道组合
由公式： \[ g(t)=\sum_{i=1}^3 f_i(t)\cos(\omega_it) \] 我们可以将这三个信号的频域进行搬移，并组合在一个信道中进行传输。其中\(\cos(\omega_it)\)就起到了幅度调制，频域搬移的作用。这是因为： \[ \begin{aligned} \mathscr{F}[f(t)\cos(\omega_0 t)]&=\frac{1}{2\pi}\mathscr{F}[f(t)]\bigotimes\mathscr{F}[\cos(\omega_0 t)]\\ &=\frac{1}{2\pi}F(\omega)\bigotimes\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]\\ &=\frac 12[F(\omega+\omega_0)-F(\omega-\omega_0)] \end{aligned} \] 在选择载波频率时，考虑到原始采样频率为\(f=10\text{Hz}\)，所以载波频率分别选择 \[ \omega_1=5,\omega_2=12.5,\omega_3=20 \] 这部分的代码是：
1 | |
同时分别画出了\(g(t)\)的时域、频域图像，如下：
时域图像：
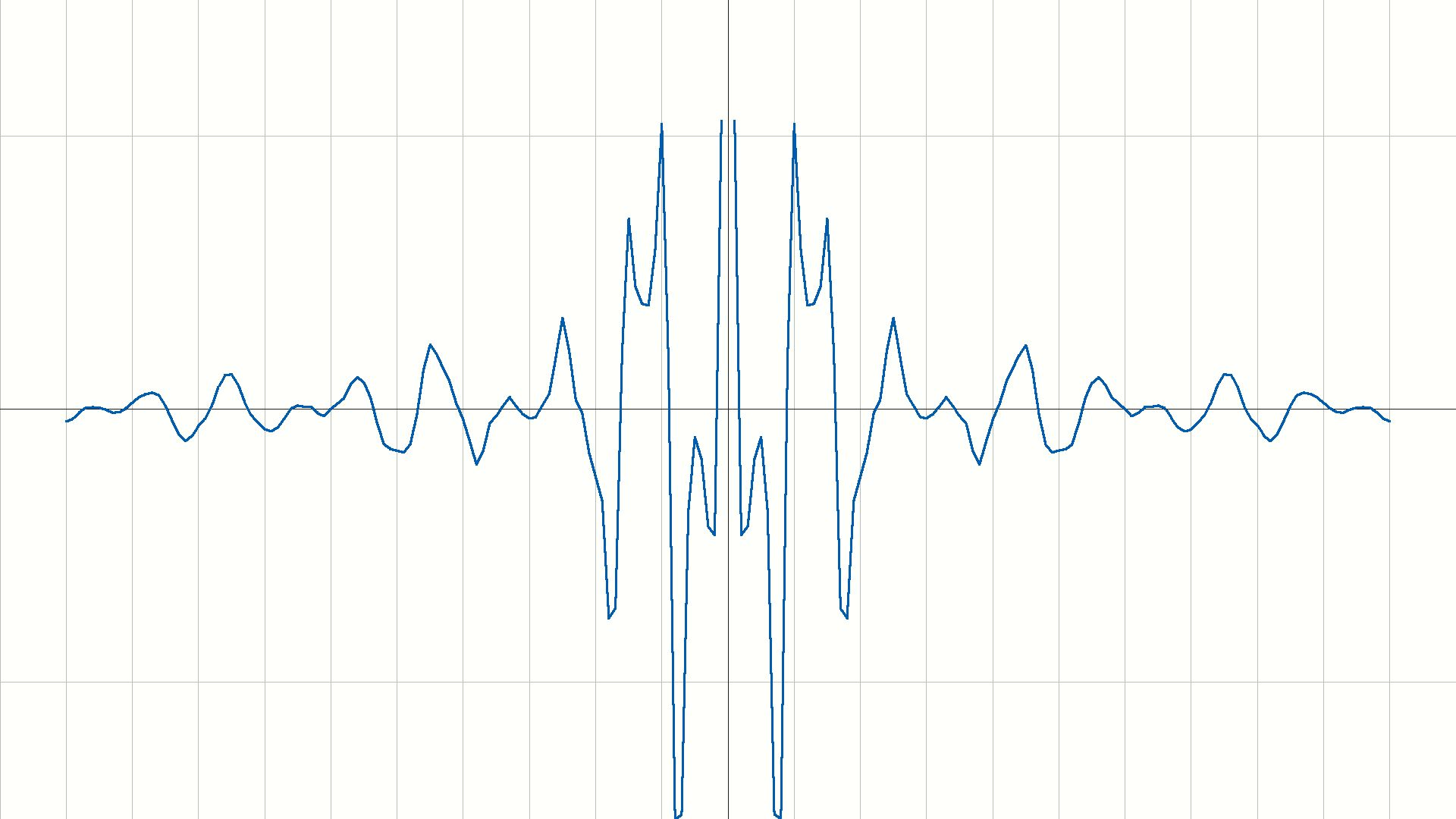
频域图像：
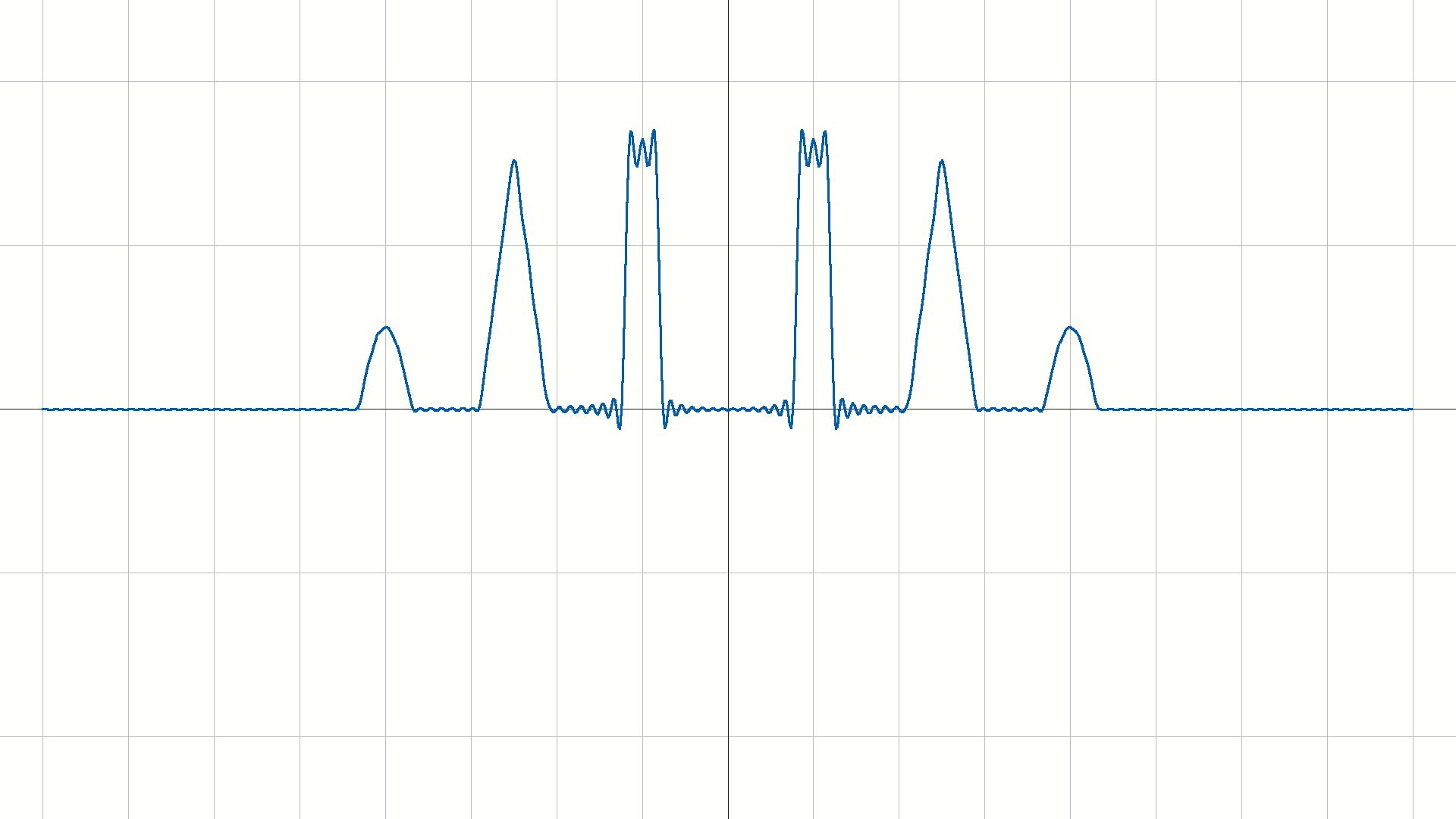
可见：已经实现了频域搬移。
使用带通滤波器接受信号
在解调过程中，使用带通滤波器接受信号。对于三个信号，分别采用中心频率为\(\omega_i\)，通过频带宽度为\(\omega_{mi}\)的带通滤波器。信号\(g(t)\)经过带通滤波器以后，被分为了三路信号。对这三路信号，每一路再乘以\(\cos(\omega_i t)\)，就把频带移动到了中间。如下图所示：
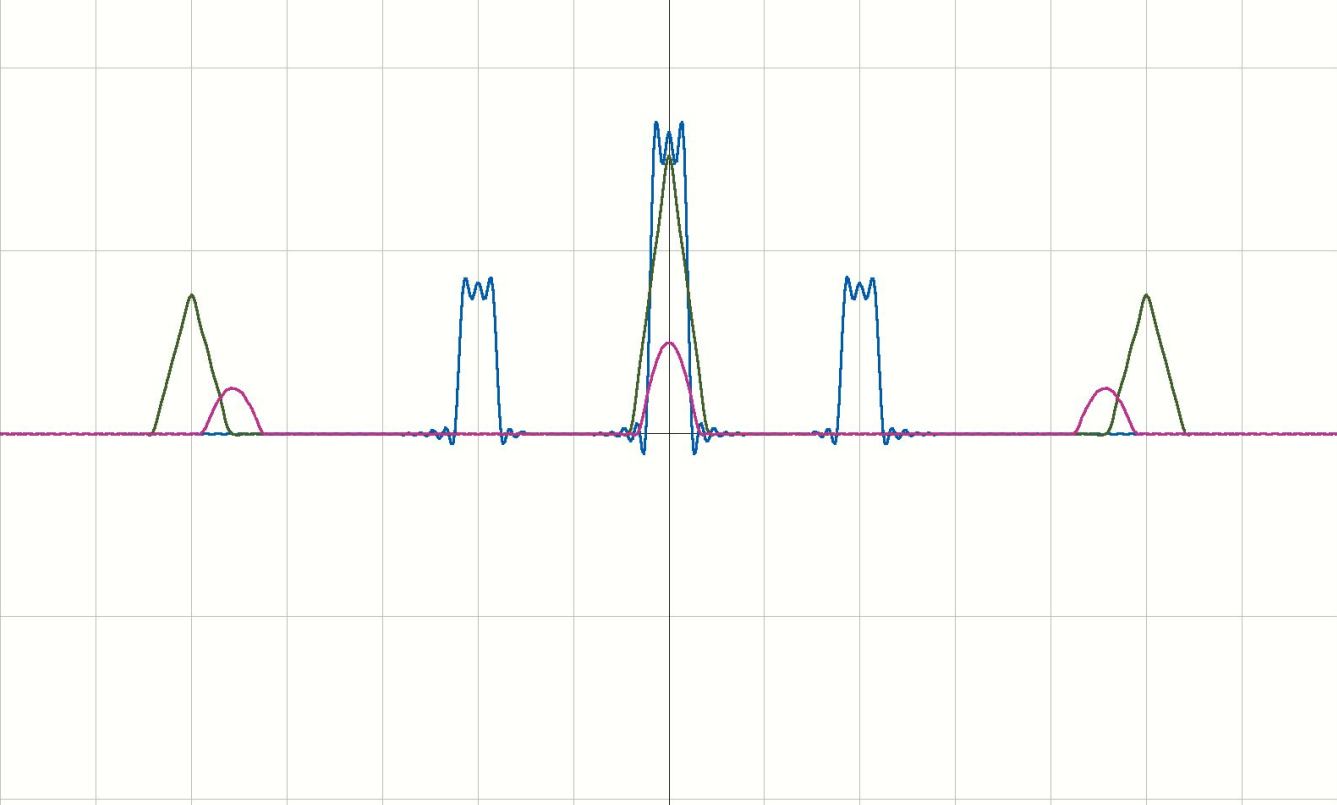
我们再对这三个信号过一个低通滤波器，就能恢复出原来的信号了。
这部分的代码如下：
通过带通滤波器分开三路信号：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15double G1[MAXN], G2[MAXN], G3[MAXN];
wF wF_g1[MAXN], wF_g2[MAXN], wF_g3[MAXN];
cnt = 0;
memset(G1, 0, sizeof(G1));
memset(G2, 0, sizeof(G2));
memset(G3, 0, sizeof(G3));
for (double w = -40; w <= 40; w += 0.1) {
G1[cnt] = G[cnt] * bandPassFilter(5.0, 5.0, w);
G2[cnt] = G[cnt] * bandPassFilter(12.5, 5.0, w);
G3[cnt] = G[cnt] * bandPassFilter(20.0, PI, w);
wF_g1[cnt] = (wF) {w, G1[cnt]};
wF_g2[cnt] = (wF) {w, G2[cnt]};
wF_g3[cnt] = (wF) {w, G3[cnt]};
++cnt;
}分别再乘以\(\cos(\omega_i t)\)再次搬移频域
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16int G1length = cnt;
cnt = 0;
double fG1[MAXN], fG2[MAXN], fG3[MAXN];
tf tf_fG1[MAXN], tf_fG2[MAXN], tf_fG3[MAXN];
for (double t = -10.0; t <= 10.0; t += 0.1) {
fG1[cnt] = fourierInvTransform(t, wF_g1, G1length);
fG2[cnt] = fourierInvTransform(t, wF_g2, G1length);
fG3[cnt] = fourierInvTransform(t, wF_g3, G1length);
fG1[cnt] *= cos(omega1 * t);
fG2[cnt] *= cos(omega2 * t);
fG3[cnt] *= cos(omega3 * t);
tf_fG1[cnt] = (tf) {t, fG1[cnt]};
tf_fG2[cnt] = (tf) {t, fG2[cnt]};
tf_fG3[cnt] = (tf) {t, fG3[cnt]};
++cnt;
}通过低通滤波器，恢复原始信号，并绘制出输出信号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29double GfG1[MAXN], GfG2[MAXN], GfG3[MAXN];
wF wf_gfg1[MAXN], wf_gfg2[MAXN], wf_gfg3[MAXN];
cnt = 0;
for (double w = -40; w <= 40; w += 0.1) {
GfG1[cnt] = fourierTransform(w, tf_fG1, g_length);
GfG2[cnt] = fourierTransform(w, tf_fG2, g_length);
GfG3[cnt] = fourierTransform(w, tf_fG3, g_length);
GfG1[cnt] *= bandPassFilter(0, 5, w)*2.0;
GfG2[cnt] *= bandPassFilter(0, 5, w)*2.0;
GfG3[cnt] *= bandPassFilter(0, 5, w)*2.0;
wf_gfg1[cnt] = (wF) {w, GfG1[cnt]};
wf_gfg2[cnt] = (wF) {w, GfG2[cnt]};
wf_gfg3[cnt] = (wF) {w, GfG3[cnt]};
++cnt;
}
length = cnt;
double finalf1[MAXN], finalf2[MAXN], finalf3[MAXN];
cnt = 0;
for (double t = -10; t <= 10; t += 0.1) {
finalf1[cnt] = fourierInvTransform(t, wf_gfg1, length);
finalf2[cnt] = fourierInvTransform(t, wf_gfg2, length);
finalf3[cnt] = fourierInvTransform(t, wf_gfg3, length);
++cnt;
}
Graph outputSignal(WIDTH, HIGHT, 0.0, 0.0, 22, 3, 1, 1, line_blue, grid, background, axis, "output.ppm");
outputSignal.drawXY(T, finalf1, cnt, line_blue);
outputSignal.drawXY(T, finalf2, cnt, line_green);
outputSignal.drawXY(T, finalf3, cnt, line_red);
return 0;
输出信号的波形如下：
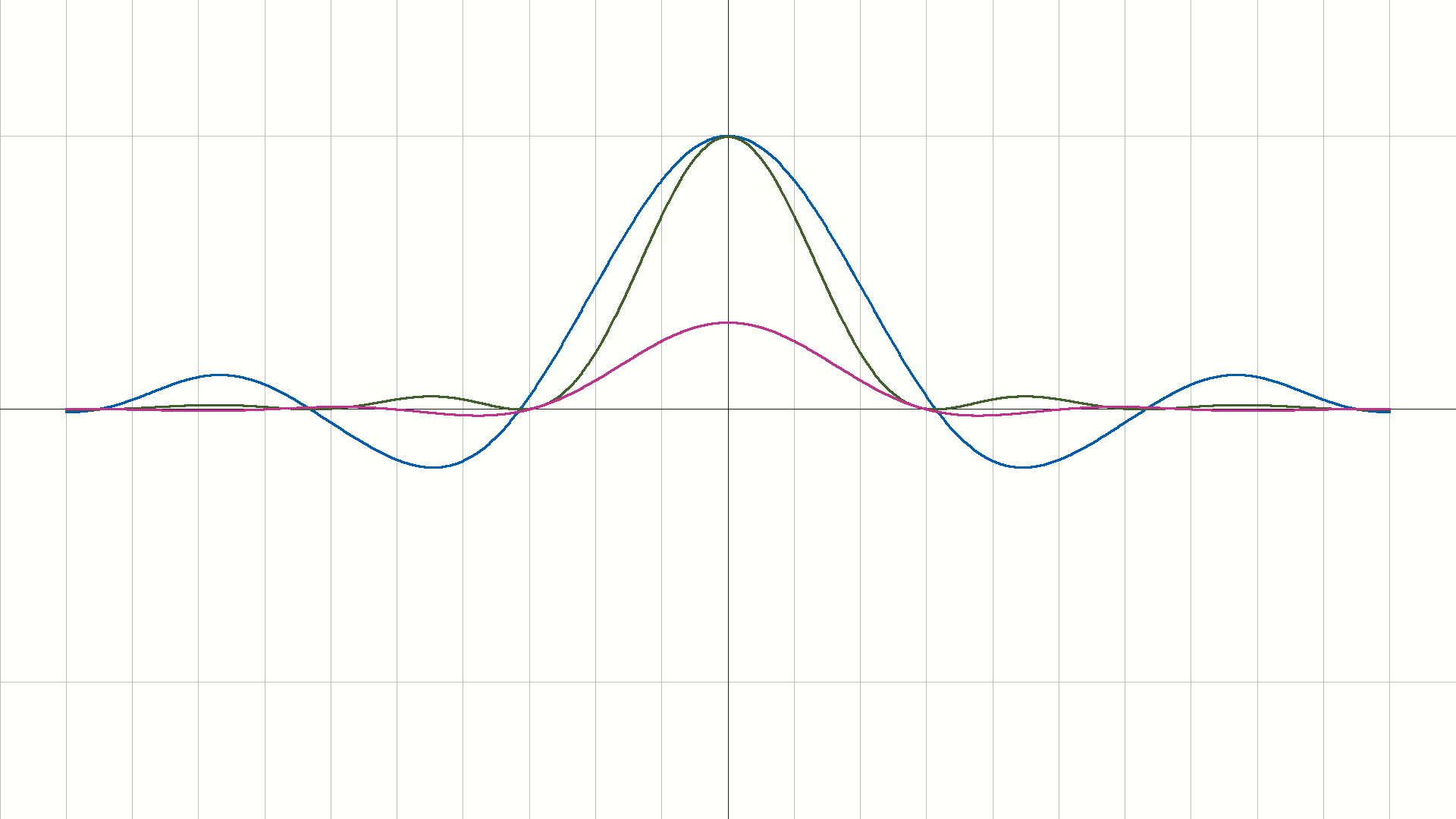
可以看出，本次实验较好地完成了频分复用信号传输的任务。
计算三个信号的均方误差，有：
1 | |
可以看出，这个系统的效果还是比较理想。
实验心得体会
本次实验我综合运用了《信号与系统》课程的相关知识，如奈奎斯特采样定理、傅里叶变换的相关内容，完成了综合信号传输系统的设计，对我的学习非常的有帮助。
附录
本次实验完整代码如下：
1 | |
"arrayToPPM2.hpp"
1 | |
信号与系统课程设计：频分复用系统设计
https://suzumiyaakizuki.github.io/2022/06/16/信号大作业/