关于平面电磁波的那些事

主要是课本和PPT的总结，加了一点点我学习时的疑问和感悟。电磁场是真™的难，能学懂的都是神人，反正我是学不懂，哈人。

@[toc]

---

平面电磁波相关概念

• 等相面：同一时刻，空间振动相位相同的点连成的面
• 等幅面：同一时刻，空间振动幅度相同的点连成的面
• 平面波：等相面是平面的波
• 均匀平面波：也叫UPW，指等相面和等幅面重合的平面波。即：在均匀平面波的等相面上，波有相同的振幅
• 球面波：等相面是球面的波
• 柱面波：等相面是柱面的波
• TEM波：电场强度和磁场强度矢量在传播方向上的分量为0的电磁波。均匀平面波一定是TEM波，反之不然。例：均匀球面波也是TEM波。

自由空间平面电磁波的时域解

由麦克斯韦方程组的推导，设源量为0，各量不随\(x,y\)变化而变化（即等相位面是\(xoy\)平面）。

由于 \[ \begin{aligned} \nabla\cdot \varepsilon_0E=0\\\\ \nabla\cdot \mu_0H=0 \end{aligned} \] 因此\(E,H\)的\(z\)分量和\(z\)无关。

由于 \[ \nabla \times H=\varepsilon \frac{\partial E} {\partial t} \] 考虑\(i_z\)分量，有： \[ \frac{\partial H_y} {\partial x}-\frac{\partial H_z} {\partial y}=\varepsilon _0\frac{\partial E_z} {\partial t}=0 \] 则\(E\)的\(z\)分量和时间无关(同理，\(H\)也是)。因此\(E_z,H_z\)是和时间，空间都没有关系的常数。在讨论时变场时不考虑常量，因此。 \[ \begin{aligned} E(z,t)=i_xE_x(z,t)+i_yE_y(z,t)\\\\ H(z,t)=i_xH_x(z,t)+i_yH_y(z,t)\\\\ \end{aligned} \] 代入麦克斯韦方程 \[ \begin{aligned} \nabla \times E=-\mu_0\frac{\partial H} {\partial t}\\\\ \nabla \times H=\varepsilon \frac{\partial E} {\partial t}\\\\ \end{aligned} \] 有 \[ \begin{cases} \frac{\partial E_y} {\partial z}=\mu_0\frac{\partial H_x} {\partial t}\\\\[2ex] \frac{\partial H_x} {\partial z}=\varepsilon_0\frac{\partial E_y} {\partial t}\\\\ \end{cases} \] 和 \[ \begin{cases} \frac{\partial E_x} {\partial z}=-\mu_0\frac{\partial H_y} {\partial t}\\\\[2ex] \frac{\partial H_y} {\partial z}=-\varepsilon_0\frac{\partial E_x} {\partial t}\\\\ \end{cases} \]

一维波动方程（以第二组为例）： \[ \begin{aligned} \frac{\partial E_x} {\partial z^2}=\mu_0\varepsilon_0\frac{\partial^2 E_x} {\partial t^2}\\\\ \frac{\partial^2 H_y} {\partial z^2}=\mu_0\varepsilon_0\frac{\partial^2H_y} {\partial t^2} \end{aligned} \] 写成统一的形式： \[ \frac{\partial^2 u} {\partial z^2}=\frac{1} {v^2}\frac{\partial ^u} {\partial t^2} \] 它的解实际上是宗量为\((z\pm vt)\)的任意二阶可微分函数，即： \[ u=f(z\pm vt) \] 那么结合麦克斯韦方程组，在电磁场中，它的解为： \[ \begin{aligned} E_x=f_1(z-vt)+f_2(z+vt)=E_x^+ + E_x^-\\\\ H_y=\sqrt{\frac{\varepsilon_0} {\mu_0} }[f_1(z-vt)-f_2(z+vt)]=H_y^+ + H_y^- \end{aligned} \] 同理，对1，有： \[ \begin{aligned} E_y=E_y^+ + E_y^-\\\\ H_x=H_x^+ + H_x^- \end{aligned} \] 那么所有沿着\(z\)传播的平面波都可以写成上面四个解的线性组合。对于\(E\)，有： \[ E=i_x(A_1E_x^+ + B_1E_x^-)+i_y(A_2E_y^+ + B_2E_y^-) \] 于是，均匀平面波有这些传播特性：

1. 电场方向和磁场方向总和波的传播方向，也就是波印庭矢量的方向垂直，即： \[ S=E\times H \]

2. 自由空间中，相速度等于光速，有： \[ v=c=(\mu_0\varepsilon_0)^{-1/2} \]

3. 空间中任意一点，电场和磁场的波形和相位都相同，而且他们的数值之比是常数，这个比叫空间波阻抗，有： \[ \eta_0=\frac{|E|} {|H|}=\sqrt{\frac{\mu_0} {\varepsilon_0} }=120\pi \]

4. 空间中任意一点，电场和磁场正交

5. 空间中任意一点，电场和磁场的能量密度相等。

## 正弦时变场和复数场定律

对于一个瞬时正弦时变场： \[ A(r,t)=i_xA_x(r)\cos\left[\omega t+\theta_x(r)\right]+i_yA_y(r)\cos\left[\omega t+\theta_y(r)\right]+i_zA_z(r)\cos\left[\omega t+\theta_z(r)\right] \] 可以借鉴“相量法”的思想，把它写成复矢量形式： \[ A(r,t)=\Re[\tilde{A}(r)e^{j\omega t}] \] 其中\(\tilde{A}(r)\)就是我们所说的正弦量的复表示。有： \[ \tilde{A}(r)=i_xA_x(r)\angle\theta_x(r)+i_yA_y(r)\angle\theta_y(r)+i_zA_z(r)\angle\theta_z(r) \] 在麦克斯韦方程组中，把对时间求导的\(\frac{\partial } {\partial t}\)换成\(j\omega\)，把各量换成复矢量表示，就得到了复数场定律。

简单媒质中复数场定律如下： \[ \begin{aligned} \nabla \times \tilde{E}(\vec{r})&=-j \omega \mu \widetilde{H}(\vec{r}) \\\\ \nabla \times \widetilde{H}(\vec{r})&=\tilde{J}_{f}(\vec{r})+j \omega \varepsilon \widetilde{E}(\vec{r}) \\\\ \nabla \cdot \varepsilon \tilde{E}(\vec{r})&=\dot{\rho}_{f}(\vec{r}) \\\\ \nabla \cdot \mu \widetilde{H}(\vec{r})&=0 \\\\ \nabla \cdot \tilde{J}_{f}(\vec{r})&=-j \omega \dot{\rho}_{f}(\vec{r}) \end{aligned} \]

正弦均匀平面波

由复数场定律可导出¹齐次亥姆霍兹方程： \[ \begin{aligned} \Delta\tilde{E}(r)+\beta^2\tilde{E}(r)=0\\\\ \Delta\tilde{H}(r)+\beta^2\tilde{H}(r)=0 \end{aligned} \] 其中 \[ \beta=\omega\sqrt{\mu\varepsilon}=\frac{2\pi} {\lambda} \] 我们知道沿\(z\)传播的均匀平面波有两组独立的解\(\dot{E}_x-\dot{H}_y\)和\(\dot{E}_y-\dot{H}_x\)，只需讨论第一组，有解： \[ \dot{E}_x(z)=\dot{E}_{m_1}e^{j\beta z}+\dot{E}_{m_2}e^{ -j\beta z} \] 结合 \[ \nabla\times\tilde{E}(r)=-j\omega\tilde{H}(r) \] 可以求出\(\dot{H}_y\).

写出对应的时域表达式，有： \[ \begin{aligned} E_x(z,t)&=\Re[\dot{E}_x(z)e^{j\omega t}]\\\\ &=|\dot{E}_{m1}|\cos(\omega t+\beta z+\alpha_1)+|\dot{E}_{m2}|\cos(\omega t-\beta z+\alpha_2)\\\\ &=|\dot{E}_{m1}|\cos\left[\beta(z+vt)+\alpha_1\right]+|\dot{E}_{m2}|\cos\left[\beta(z-vt)+\alpha_2\right] \end{aligned} \] 其中\(\alpha\)是\(\dot{E}_m\)的幅角。于是，各项的物理意义便很明显了：复振幅\(\dot{E}_m\)反映了电场在\(z=0\)点的初始振幅和相位，而\(e^{\pm j\beta z}\)反映了相位随空间位置的变化和波的传播情况。其中\(\beta\)称为空间相位常数。

复数场极化方向的判断

电场的极化方向也就是说电场矢量尖端在和电磁场传播方向垂直的平面上划出的轨迹形状。有圆、椭圆、线极化三种。在判断复数场的极化方向时，有以下的操作步骤。

对于复数场 \[ \begin{aligned} \tilde{E}(r)&=\dot{E}_me^{-j\beta z}\\\\ &=[E_R(z)+j\cdot E_I(z)]e^{-j\beta z} \end{aligned} \]

1. 线极化：以下三条件任意满足一项 \[ E_R(z)=0,\ E_I(z)=0, E_R(z)//E_I(z) \]

2. 圆极化：同时满足以下条件 \[ E_R(z)\cdot E_I(z)=0 ,\ |E_R(z)|=|E_I(z)| \]

3. 椭圆极化：其余情况。

判断左旋还是右旋的方法是：在右手系（即右手从\(x\)轴握向\(y\)轴，大拇指指向\(z+\)方向）中，画出电磁场传播方向（也就是波因亭矢量的方向）、\(E_R\)、\(E_I\)，然后用右手从\(E_I\)向\(E_R\)握，如果大拇指指向\(S\)，那么就是右旋，否则是左旋。

空间任意方向电磁场的表达

前面我们讨论的都是沿着\(z\)轴的电磁场。如果指向\(i_xa+i_yb+i_zc\)的电磁场，我们就要改变\(e\)的指数。有： \[ \tilde{E}(r)=\dot{E}_me^{-j(ax+by+cz)} \] 这时，\(\beta=\sqrt{a^2+b^2+c^2}\).

通过例题来感受一下。

【例】已知均匀平面波的电场为 \[ E(\boldsymbol{r},t)=10(i_x+2i_y+E_zi_z)\cos(\omega t+3x-y-z) \] 求：传播方向（用单位矢量表示），波长，角频率，极化状态，磁场（用复矢量表示）

【解】 \[ \begin{aligned} \tilde{E}(\boldsymbol{r})&=\dot{E}_0e^{-j\boldsymbol{\beta \cdot r} }\\\\ &=10(i_x+2i_y+E_zi_z)e^{-j(-3x+y+z)}\\\\ \end{aligned} \] 波的传播方向： \[ \boldsymbol{i}_\beta=\frac{\boldsymbol{\beta} } {|\boldsymbol{\beta}|}=\frac{-3i_x+i_y+i_z} {\sqrt{3^2+1+1} }=\left(\frac{-3} {\sqrt{11} },\frac 1{\sqrt{11} },\frac 1{\sqrt{11} }\right) \] 波长： \[ \lambda=\frac{2\pi} {\beta}=\frac{2\pi} {\sqrt{11} }=1.89\text{(m)} \] 角频率： \[ \omega=\beta c=3\sqrt{11}\times 10^8 \text{(rad/s)} \] 由于电场方向和电磁场传播方向应该正交，即： \[ \boldsymbol{\beta}\cdot \dot{E}_0=0 \] 则解得\(E_z=1\)

由于满足 \[ \Im[E_0]=0 \] 因此是线极化波。

由 \[ H=\frac 1{\eta_0}i_\beta\times\tilde{E}(r,t) \] 可求得\(H\).

复数形式场的功率讨论

复矢量乘积的意义

容易证明：两个复矢量的共轭叉（点）积的实部的一半等于相应的正弦时变量叉（点）积的时间平均值。

即： \[ \langle\vec{A}(t) \times \vec{B}(t)\rangle=\frac{1} {2} \operatorname{Re}\left(\tilde{A} \times \tilde{B}^{*}\right) \]

\[ \langle\vec{A}(t) \cdot \vec{B}(t)\rangle=\frac{1} {2} \operatorname{Re}\left(\tilde{A} \cdot \tilde{B}^{*}\right) \]

证明提示：

用公式 \[ \vec{A}(t)=\frac{1} {2}\left[\tilde{A} e^{j \omega t}+\tilde{A}^{*} e^{-j \omega t}\right] \] 把时变量运算式中的时变量和复矢量关联起来。

复数坡印廷矢量

在前面，我们学过时域坡印廷矢量： \[ \boldsymbol{S}(\boldsymbol{r},t)=\boldsymbol{E}(\boldsymbol{r},t)\times\boldsymbol{H}(\boldsymbol{r},t) \] 将电场，磁场的时域表达式用复数形式来表示，即： \[ \begin{aligned} \boldsymbol{E}(\boldsymbol{r},t)=\frac 12[\tilde{E}(r)e^{j\omega t}+\tilde{E}^*(r)e^{-j\omega t}]\\\\ \boldsymbol{H}(\boldsymbol{r},t)=\frac 12[\tilde{H}(r)e^{j\omega t}+\tilde{H}^*(r)e^{-j\omega t}] \end{aligned} \] 代入： \[ \boldsymbol{S}(\boldsymbol{r},t)=\frac 12\Re[\tilde{E}(r)\times \tilde{H}^*(r)]+\frac 12\Re[\tilde{E}(r)\times \tilde{H}^*(r)2^{j2\omega t}] \] 定义复数坡印廷矢量： \[ \tilde{S}(r)=\frac 12 \tilde{E}(r)\times\tilde{H}^*(r) \] 则有： \[ \frac 12\Re[\tilde{E}(r)\times \tilde{H}^*(r)]=\langle S(r,t)\rangle=\Re[\tilde{S}(r)] \] 于是，我们可以说：复数坡印廷矢量的实部表示有功功率流密度，虚部可以解释为无功功率流密度。（这里可以类比电路分析中的复功率\(\dot{P}=\dot{V}_m\dot{I}_m/2=P+jQ\)）

复数坡印廷定理

复数坡印廷定理的微分形式表达式如下： \[ -\nabla \cdot \tilde{S}(\vec{r})-\frac{1} {2}\left[\tilde{E}(\vec{r}) \cdot \tilde{J}_{S}^{*}(\vec{r})\right]=\frac{1} {2}\left[\tilde{E}(\vec{r}) \cdot \tilde{J}_{d}^{*}(\vec{r})\right]+j 2 \omega\left[\frac{\mu} {4}|\widetilde{H}(\vec{r})|^{2}-\frac{\varepsilon} {4}|\tilde{E}(\vec{r})|^{2}\right] \] 为了理解其中各项物理意义，解释如下：

• 等号左边第二项 \[ \Re\left[-\frac 12\tilde{E}(\vec{r}) \cdot \tilde{J}_{S}^{*}(\vec{r})\right]=\langle J_s(r,t)\times E(r,t)\rangle=\langle p_s(r,t)\rangle \] 这一项表示电源提供的有功功率

• 等号右边第一项 \[ \Re\left[\frac 12\tilde{E}(\vec{r}) \cdot \tilde{J}_{d}^{*}(\vec{r})\right]=\langle p_d(r,t)\rangle \] 这一项表示电阻消耗的功率（即焦耳热功率）。注意：因为 \[ \frac 12\tilde{E}(\vec{r}) \cdot \tilde{J}_{d}^{*}(\vec{r})=\frac 12\sigma |\tilde{E}(r)|^2 \] 所以这一项实际上是纯实数。

• 等号右边第二项 \[ \frac{\mu} {4}|\widetilde{H}(\vec{r})|^{2}=\langle\frac 12 \mu H(r,t)\cdot H(r,t)\rangle=\langle w_m(r,t)\rangle \] 这一项可以理解为电感能量，也是纯实数（乘以前面的系数就是纯虚数了）

• 等号右边第三项 \[ \frac{\varepsilon} {4}|\tilde{E}(\vec{r})|^{2}=\langle\frac 12 \varepsilon E(r,t)\cdot E(r,t)\rangle=\langle w_e(r,t)\rangle \] 这一项可以理解为电容的能量。

我们把上面那个式子的实部和虚部拆开，有：

• 实部： \[ \langle-\nabla \cdot \vec{S}(\vec{r}, t)\rangle+\left\langle p_{s}(\vec{r}, t)\right\rangle=\left\langle p_{d}(\vec{r}, t)\right\rangle \] 电磁场向某点提供的电磁功率密度的时间平均值（有功电磁功率密度）与电源向该点提供的电磁功率密度的时间平均值（有功电磁功率密度）之和，等于该点焦耳热损耗功率密度的时间平均值。

• 虚部 \[ -\operatorname{Im}[\nabla \cdot \tilde{S}(\vec{r})]+q_{S}(\vec{r})=2 \omega\left[\left\langle w_{m}(\vec{r}, t)\right\rangle-\left\langle w_{e}(\vec{r}, t)\right\rangle\right] \] 电磁场和电源向某点提供的无功电磁功率密度等于该点的磁能功率密度时间平均值和电能功率密度时间平均值之差的\(2𝜔\)倍

平面波在有耗媒质中的传播

有耗媒质的根本特征是其电导率\(\sigma\)不为零，进而，其中的传导电流\(J_d\)不为零。因此，电磁波在其中传播时会产生损耗。特别的，如果电导率很高，以至于成为导体（例如金属），那么电磁波在其中几乎不能传播，只能在表面传播，这叫做“趋肤效应”。电磁波不能在理想导体中传播。

考虑复数形式的修正安培环路定律： \[ \nabla \times \tilde{H}(r)=\tilde{J}+j\omega \varepsilon\tilde{E}(r) \] 将 \[ \tilde{J}=\sigma\tilde{E}(r) \] 代入，有： \[ \nabla \times \tilde{H}(r)=\sigma\tilde{E}(r)+j\omega \varepsilon\tilde{E}(r)=j\omega\left(\frac{\sigma} {j\omega}+\varepsilon\right)\tilde{E}(r) \] 定义复介电常数： \[ \dot{\varepsilon}=\left(\frac{\sigma} {j\omega}+\varepsilon\right) \] 用复介电常数替换复麦克斯韦方程组中所有的介电常数，就能得到有耗媒质中的场定律。

需要注意的是，这时候波阻抗也变成了复数，即： \[ \dot{\eta}=\frac{\mu} {\dot{\varepsilon} } \] 仿照前面的过程²，导出复亥姆霍兹方程。仿照传播常数(波数)\(\beta\)，定义复传播常数 \[ \dot{k}=\omega\sqrt{\dot{\varepsilon}\mu}=\beta-j\alpha \] 那么，在有耗媒质中传播的电磁波的电场和磁场的复表示如下： \[ \begin{aligned} &\widetilde{E}(r)=\hat{\imath}_{x} \dot{E}_{x 0} e^{-\alpha z} e^{-j \beta z}=\hat{\imath}_{x}\left|\dot{E}_{x 0}\right| e^{j \varphi_{x 0} } e^{-\alpha z} e^{-j \beta z} \\\\ &\widetilde{H}(r)=\hat{\imath}_{y} \frac{\dot{E}_{x 0} } {\dot{\eta} } e^{-\alpha z} \cdot e^{-j \beta z}=\hat{\imath}_{y}\left|\frac{\dot{E}_{x 0} } {\dot{\eta} }\right| e^{j\left(\varphi_{x 0}-\varphi_{\eta}\right)} e^{-\alpha z} e^{-j \beta z} \end{aligned} \] 这里之所以要特意把\(\dot{E}_{x0}\)以及\(\dot{E}_{x0}/\dot{\eta}\)拆开成模长-幅角模式来写，是为了体现平面波在有耗媒质中的传播特点。

在有耗无源简单媒质中传播的均匀平面波是一个沿传播方向衰减的均匀平面波，衰减因子用\(\alpha\)表示。电磁波频率越高，衰减因子越大，最终会趋向于 \[ \max \alpha=\frac {\sigma} {2}\sqrt{\frac{\mu} {\varepsilon} } \] 且磁场与电场不再同相。这是因为波阻抗不再是实数。

导体的趋肤效应

导体的电导率\(\sigma\)越大，衰减因子也就越大。透入深度表示幅度衰减为\(e^{-1}\)的深度，对良导体，其值为： \[ \delta=\sqrt{\frac 2{\omega\sigma\mu} } \]

平面波的反射和折射

相关概念

• 入射线：入射波波矢量\(\boldsymbol{\beta}_i\)所在的直线

• 入射面：同时包含入射线和界面法线的平面

• 入射角：入射线和法线的夹角

• 反射线：反射波波矢量\(\boldsymbol{\beta}_r\)所在的直线

• 反射面：同时包含反射线和界面法线的平面

• 反射角：反射线和法线的夹角

• 折射线：折射波波矢量\(\boldsymbol{\beta}_\tau\)所在的直线

• 折射角：折射线和界面法线的夹角

• 垂直极化：线极化波的电场和入射面垂直

• 平行极化³：线极化波的电场和入射面平行

• 媒质的折射指数（折射率）： \[ n=\sqrt{\mu_r\varepsilon_r} \] 其中\(\mu_r,\varepsilon_r\)是相对磁导率和相对介电常数⁴。

• 媒质的波数： \[ \beta=\omega\sqrt{\mu_1\varepsilon_1}=\beta_0n_1 \]

• 媒质的波阻抗： \[ \eta_1=\sqrt{\frac{\mu_1} {\varepsilon_1} }=\eta_0\sqrt{\frac{\mu_{r1} } {\varepsilon_{r1} }} \]

• Snell定律

  • 反射线和折射线都在入射面内
  • 反射角等于入射角
  • 折射角和入射角的正弦之比等于折射率之比，也等于波数之比和波的传播速度之比。

• 光密（疏）介质：一个媒质的折射指数（折射率）越大，光（电磁波）在其中传播的速度越慢，波数\(\beta\)越大，它就越可以被称为光密介质。真空是最疏的介质。

自由空间和理想导体界面的反射

正入射

img

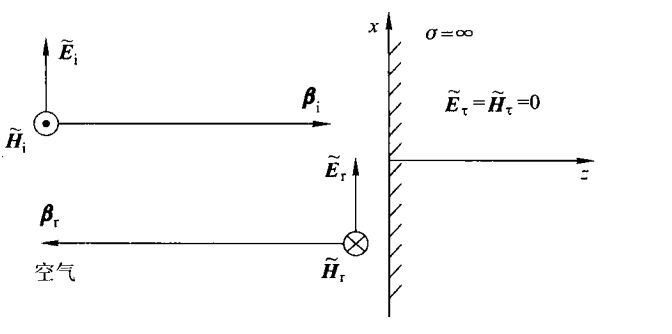
如图所示，入射波为 \[ \begin{aligned} \tilde{E}(r)=i_x\dot{E}_{i0}e^{-j\beta_0z}\\\\ \tilde{H}(r)=i_y\frac{\dot{E}_{i0} } {\eta_0}e^{-j\beta_0z} \end{aligned} \] 那么反射波的形式为： \[ \begin{aligned} \tilde{E}_r(r)=i_x\dot{E}_{r0}e^{j\beta_0z}\\\\ \tilde{H}_r(r)=i_y\frac{\dot{E}_{r0} } {\eta_0}e^{j\beta_0z} \end{aligned} \] 下面求\(\dot{E}_{r0}\)。由边界条件： \[ i_n\times(\tilde{E}_1-\tilde{E}_2)=0 \] 其中： \[ \begin{aligned} \tilde{E}_1&=\tilde{E}_i+\tilde{E}_r\\\\ \tilde{E}_2&=0\\\\ i_n&=-i_z \end{aligned} \] 代入，得： \[ \dot{E_{r0} }=-\dot{E}_{i0} \] 则有： \[ \begin{aligned} \tilde{E}_r(r)=-i_x\dot{E}_{i0}e^{j\beta_0z}\\\\ \tilde{H}_r(r)=-i_y\frac{\dot{E}_{i0} } {\eta_0}e^{j\beta_0z} \end{aligned} \] 合成波表达式为⁵： \[ \begin{aligned} \tilde{E}(r)=-2j\cdot i_x \dot{E}_{i0}\sin \beta_0z\\\\ \tilde{H}(r)=2\cdot i_y\frac{\dot{E}_{i0} } {\eta_0}\cos \beta_0z \end{aligned} \] 为了研究合成波的性质，我们把它转换到时域： \[ \begin{aligned} E(r,t)=i_x\cdot2|\dot{E}_{i0}|(\sin\beta_0z)\sin(\omega t+\varphi)\\\\ H(r,t)=i_y\cdot\frac{2} {\eta_0}|\dot{E}_{i0}|(\cos\beta_0z)\cos(\omega t+\varphi) \end{aligned} \] 我们可以看到，这表达了一列驻波。在驻波中电场和磁场有所谓“三个90度”关系，即：

• 电场和磁场在空间分布上的相位差为90度。这说明：电场最强的 地方 磁场最弱。
• 电场和磁场在时间分布上的相位差为90度。这说明：电场最强的 时刻 磁场最弱。
• 电场和磁场在空间方向上相差90度。

在驻波中，没有能量指向性的传播，只有能量形式的转换。

斜入射

首先以垂直极化为例分析问题：

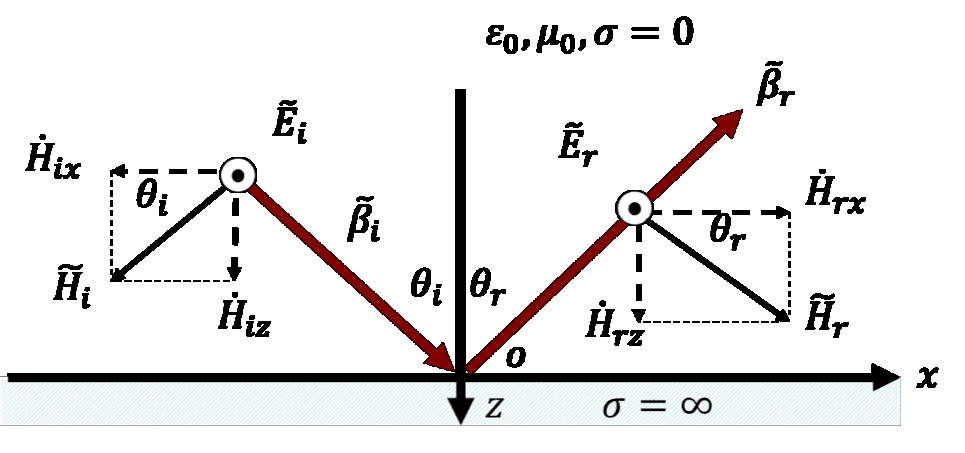
特别注意：不要看着这张图上面画了线，就以为电磁波“只在那条线上存在”，我们这里讨论的是平面波，入射波、反射波都在\(z<0\)整个空间上存在，所以可以直接合成，不需要也不应该考虑位置。

入射方向： \[ \vec{\beta}_{i}=\beta_{0}\left(i_{x} \sin \theta_{i}+i_{z} \cos \theta_{i}\right) \] 反射方向： \[ \vec{\beta}_{r}=\beta_{0}\left(i_{x} \sin \theta_{r}-i_{z} \cos \theta_{r}\right) \] 那么，分别有入射场和反射场： \[ \begin{aligned} \tilde{E}_{i} &=i_{y} \dot{E}_{i 0} e^{-j \vec{\beta}_{i} \cdot \vec{r} }=i_{y} \dot{E}_{i 0} e^{-j \beta_{0}\left(x \sin \theta_{i}+z \cos \theta_{i}\right)} \\\\ \tilde{E}_{r} &=i_{y} \dot{E}_{r 0} e^{-j \beta_{0}\left(x \sin \theta_{r}-z \cos \theta_{r}\right)} \end{aligned} \] 由边界条件计算，得： \[ \dot{E}_{r0}=-\dot{E}_{i0} \] 那么空间中的合成电场为：

$$ \[\begin{aligned} \tilde{E}&=\tilde{E}_{i}+\tilde{E}_{r}=i_{y}\left[\dot{E}_{i 0} e^{-j \beta_{0}(x \sin \theta+z \cos \theta)}-\dot{E}_{i 0} e^{-j \beta_{0}(x \sin \theta-z \cos \theta)}\right]\\\\ &=i_{y} \dot{E}_{i 0}\left(e^{-j \beta_{0} z \cos \theta}-e^{j \beta_{0} z \cos \theta}\right) e^{-j \beta_{0} x \sin \theta}\\\\ &=-i_{y} \dot{E}_{i 0} j 2 \sin \left(\beta_{0} z \cos \theta\right) e^{-j \beta_{0} x \sin \theta} \end{aligned}\]

$$

记 \(\beta_0\cos \theta=\beta_z,\beta_0\sin\theta=\beta_x\) ，有：

\[ \tilde{E}=-i_{y} 2 j \dot{E}_{i 0} \sin \beta_{z} z \cdot e^{-j \beta_{x} x} \]

再由麦克斯韦方程组可求得磁场。

观察\(\tilde{E}\)的表达式，我们发现有以下特点：

1. 在\(x\)是常数的平面上，\(e^{-j\beta_xx}\)是常数，所以\(x=C\)是波的等相面。在\(x=C\)的平面上，场量按三角函数形式分布，波显示出驻波性质。
2. 在\(z\)是常数的平面上，\(\sin \beta_zz\)是常数，波的表达式表现出一般平面波的形式，是行波。而且在等相面上振幅不是常数，是非均匀平面波。
3. 于是，我们可以发现：合成波只在\(x\)方向有能量传输，而在\(z\)方向没有。

正入射时，入射波和反射波的合成波形成了一种特殊的传播方式，我们称之为驻波。 斜入射时，入射波和反射波的合成波也形成了一种特殊的传播方式，我们称之为导行波。 这里的电场指向\(y\)，和传播方向垂直，我们称之为横电波（TE波）。

导行波的等相面是 \[ \omega t-\beta_x x=C \] 因此，其相速度为 \[ v_p=\frac c {\sin\theta} \] 神奇！相速度超过了光速！但是我们都知道光速是无论如何不能超过的，这是怎么回事呢？我们要先理解相速度和群速度。

这个图片只用来说明相速度和群速度的概念

• 相速度是等相位面传播的速度，也就是图中红色方块的速度。
• 群速度的波包移动的速度，是能量传递的速度，也就是绿色圆点移动的速度。

我们可以看出，只有群速度是真正的速度。譬如说，我拿着一个激光笔扫过夜空，那么激光笔在云层上反射的光点可能会具有非常非常非常高的速度，那么难道说真的有物体在以这个速度移动吗？不是这样的。相速度只是一种“看起来”的速度，是一个虚假的速度。

img

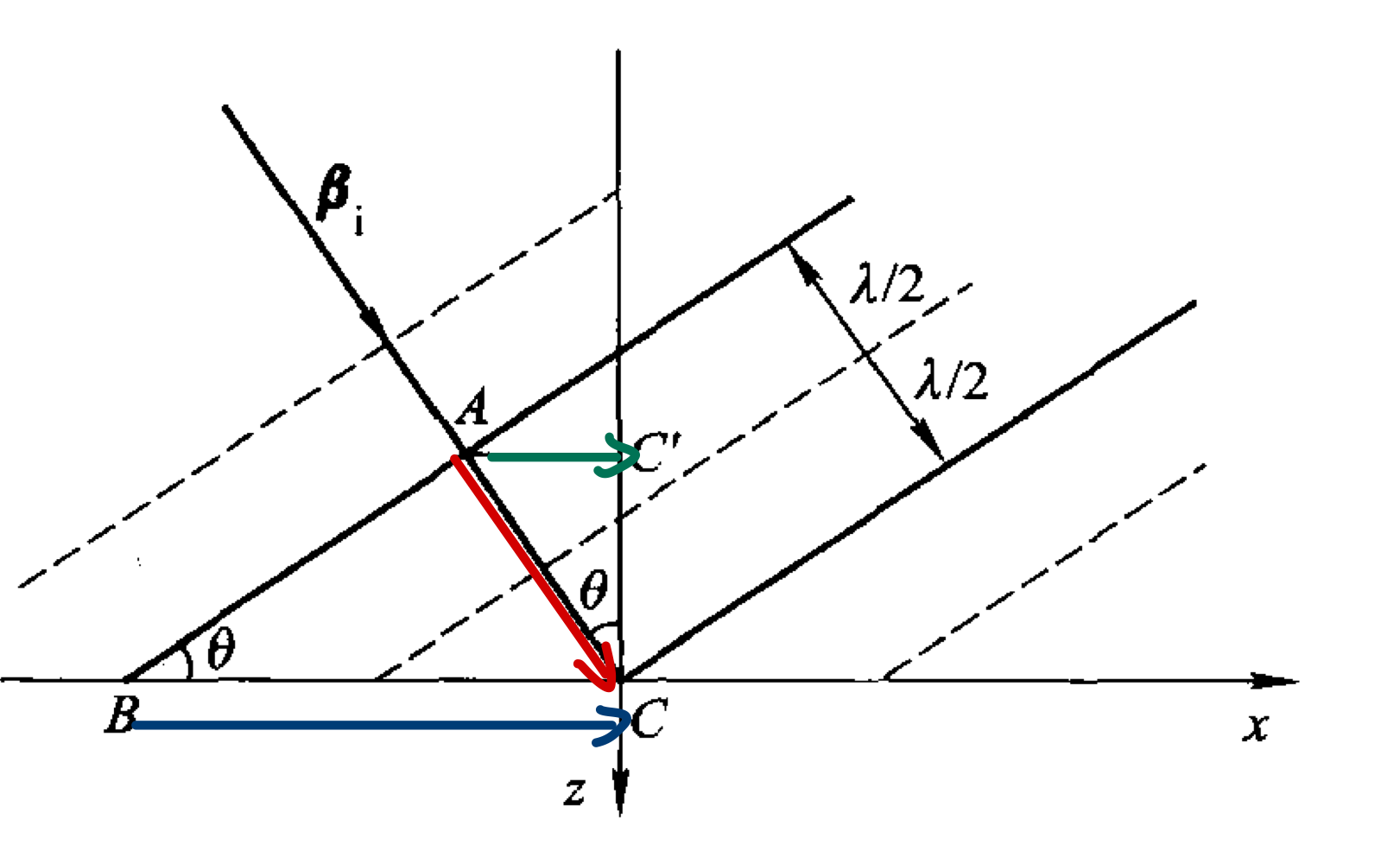
如图，在这个情景中，黑色的实线和虚线是等相位面，蓝色是相速度，绿色是群速度，红色是光速。这么一说大家应该可以理解了。在一个周期里，导行波过\(A\)点的等相位面的相位传到了\(C\)点，从\(X\)方向看，就像是相位从\(B\)移动到了\(C\)，而此时能量只是从A移动到了\(C’\)。

在平行极化时，合成波的磁场是横向的，电场是\(xOz\)面内的椭圆极化波。合成波依然在\(x\)方向表现行波，在\(z\)方向表现为驻波。这种波叫横磁波（TM波）。

在两种理想介质分界面处的反射和折射

这里讨论的是两种均匀、线性、各向同性、无耗理想介质分界面处的反射和折射。

两种无耗介质交界面的垂直入射

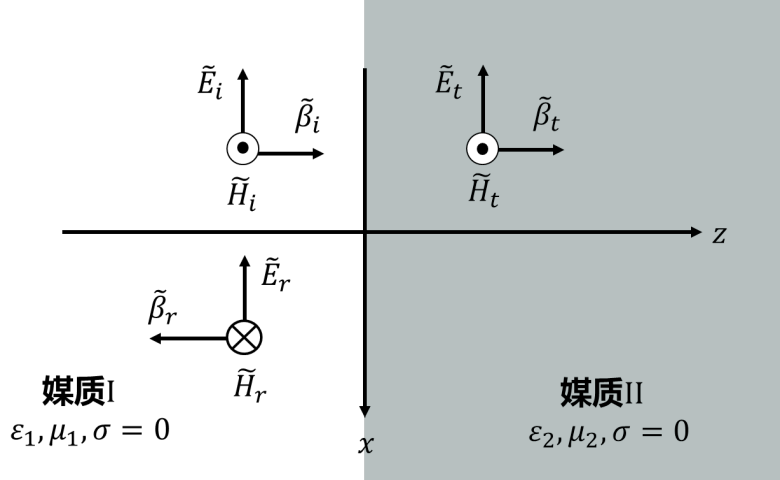
入射波为 \[ \begin{aligned} \tilde{E}(r)=i_x\dot{E}_{i0}e^{-j\beta_0z}\\\\ \tilde{H}(r)=i_y\frac{\dot{E}_{i0} } {\eta_0}e^{-j\beta_0z} \end{aligned} \] 不难写出反射波，折射波的表达式：只需要把入射波中的\(E_{i0}\)换成\(E_{r0},E_{\tau 0}\)，再注意一下方向就行了，十分的简单。我们的问题现在是：\(E_{i0}\)和\(E_{r0},E_{\tau 0}\)的关系是？

由边界条件： \[ \begin{aligned} i_{n} \times\left.\left(\tilde{E}_{1}-\tilde{E}_{2}\right)\right|_{z=0}=0 \quad \\\\ i_{n} \times\left.\left(\widetilde{H}_{1}-\widetilde{H}_{2}\right)\right|_{z=0}=\tilde{k}_{f}=0 \end{aligned} \] 得： \[ \left\{\begin{array} {l} \dot{E}_{i 0}+\dot{E}_{r 0}=\dot{E}_{\tau 0} \\\\ \dot{H}_{i 0}-\dot{H}_{r 0}=\dot{H}_{\tau 0} \Rightarrow \frac{\dot{E}_{i 0} } {\eta_{1} }-\frac{\dot{E}_{r 0} } {\eta_{1} }=\frac{\dot{E}_{\tau 0} } {\eta_{2} } \end{array}\right. \]

于是有反射系数： \[ \Gamma=\frac{\dot{E}_{r 0} } {\dot{E}_{i 0} }=\frac{\eta_{2}-\eta_{1} } {\eta_{2}+\eta_{1} } \] 透射系数： \[ T=\frac{\dot{E}_{\tau 0} } {\dot{E}_{i 0} }=\frac{2 \eta_{2} } {\eta_{2}+\eta_{1} } \]

三层介质垂直入射无反射条件

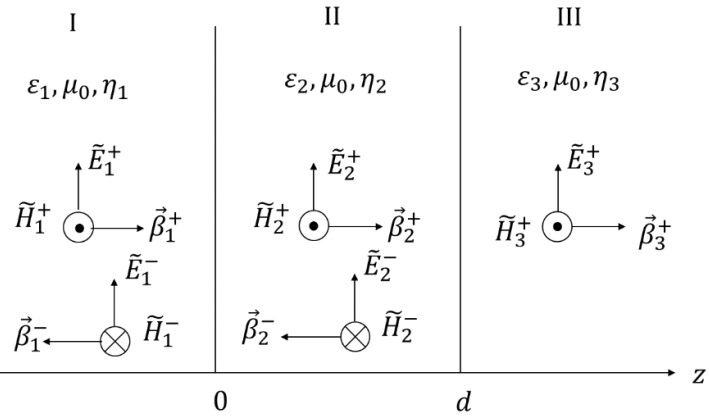
一般来说应用场景是：I是空气（真空），III是玻璃，II是增透膜，要求你调整增透膜的\(\eta_2\)和厚度。有以下两种情况都能达到目的：

1. \(\eta_1=\eta_3,d=n\lambda_2/2\)
2. \(\eta_2=\sqrt{\eta_1\eta_3},d=(2n+1)\lambda_2/4\)

请注意，这里的波长是在介质2中的波长。电磁场在不同介质中，频率是不会变 ，而波长会变。

斜入射

还是以垂直极化为例：

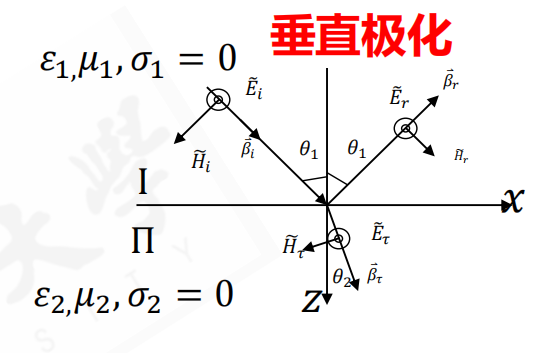
同样，由边界条件计算反射、透射系数，有：

反射系数： \[ \Gamma_{\perp}=\frac{\dot{E}_{r 0} } {\dot{E}_{i 0} }=\frac{\eta_{2} \cos \theta_{1}-\eta_{1} \cos \theta_{2} } {\eta_{2} \cos \theta_{1}+\eta_{1} \cos \theta_{2} } \]

透射系数： \[ T_{\perp}=\frac{\dot{E}_{\tau 0} } {\dot{E}_{i 0} }=\frac{2 \eta_{2} \cos \theta_{1} } {\eta_{2} \cos \theta_{1}+\eta_{1} \cos \theta_{2} } \]

有时候会出现一些神奇的现象：

• 全反射

  全反射无论是磁介质（\(\mu_r\neq 1\)）还是电介质（\(\varepsilon_r\neq 1\)）都可以产生。当从光密介质射入光疏介质时，当入射角达到一个临界值\(\theta_c\)时，反射线和介质表面重合（反射角是\(\pi/2\)），这时称为出现全反射现象，\(\theta_c\)是全反射临界角。有： \[ \sin \theta_c=\frac{n_2} {n_1} \]

• 全折射 当入射波垂直极化时，在电介质交界面，不会出现全折射现象，只有磁介质交界面才会出现。无论从疏到密，还是从密到疏，都能发生全折射现象。全折射的临界角\(\theta_{P_\perp}\)称为布茹斯特角。有： \[ \theta_{P_\perp}=\sqrt{\frac{\mu_2} {\mu_1+\mu_2} } \]

我写了一个代码来计算反射系数和折射系数：

er1=Input["介质1的相对介电常数"];
mur1=Input["介质1的相对磁导率"];
er2=Input["介质2的相对介电常数"];
mur2=Input["介质2的相对磁导率"];
eta0=120*Pi;
eta1=eta0*Sqrt[mur1/er1];eta2=eta0*Sqrt[mur2/er2];
n1=Sqrt[mur1*er1];n2=Sqrt[mur2*er2];
Rfl[theta]:=ArcSin[Sin[theta]*n1/n2];
Gammaa[theta]:=(eta2*Cos[theta]-eta1*Cos[Rfl[theta]])/(eta2*Cos[theta]+eta1*Cos[Rfl[theta]]);
Tt[theta]:= (2*eta2*Cos[theta])/(eta2*Cos[theta]+eta1*Cos[Rfl[theta]]);
Plot[{Abs[Gammaa[theta]],Abs[Tt[theta]]},{theta,0,Pi/2},PlotLegends->"Expressions"]

例如，输入

3 1 1 1

会给出图像

全反射现象示意图

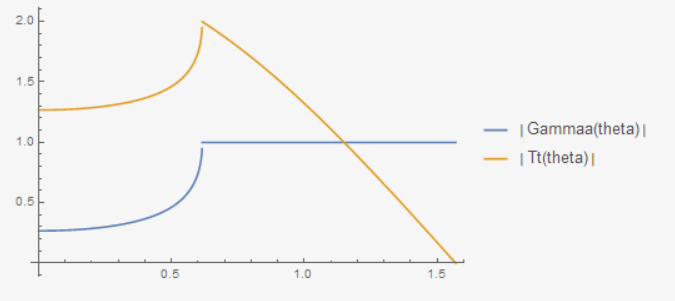
全反射现象十分明显。

再例如输入

1 1 1 3

会给出图像

全折射现象示意图

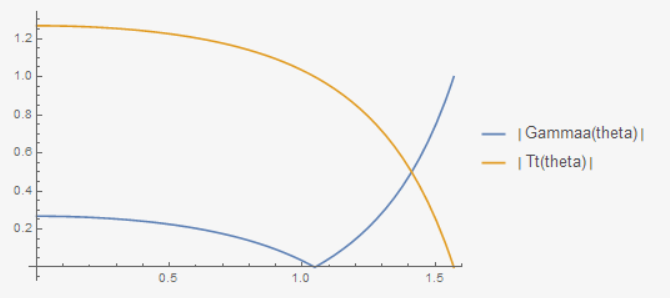
从疏介质射入密介质，这里发生了全折射。

---

---

1. 由于\(\nabla\times\tilde{E}(r)=-j\omega\mu\tilde{H}(r)\)，两边取旋度，有\(\nabla\times\nabla\times\tilde{E}(r)=-j\omega\mu\nabla \times \tilde{H}(r)\)，代入\(\nabla \times \tilde{H}(r)=j\omega\varepsilon\tilde{E}(r)\)，并结合矢量公式\(\nabla\times\nabla\times A=\nabla[\nabla \cdot A]-\Delta A\)即可推出。↩︎

2. 由于\(\nabla\times\tilde{E}(r)=-j\omega\mu\tilde{H}(r)\)，两边取旋度，有\(\nabla\times\nabla\times\tilde{E}(r)=-j\omega\mu\nabla \times \tilde{H}(r)\)，代入\(\nabla \times \tilde{H}(r)=j\omega\varepsilon\tilde{E}(r)\)，并结合矢量公式\(\nabla\times\nabla\times A=\nabla[\nabla \cdot A]-\Delta A\)即可推出。↩︎

3. 椭圆极化波和圆极化波可以分解成两个垂直的线极化波，进而，可以分解成垂直极化和平行极化波。↩︎

4. 相对磁导率（介电常数）意思是媒质中的磁导率（介电常数）和真空中的比值。↩︎

5. \(\sin x=\frac{1} {2j}(e^{jx}-e^{-jx})\),\(\cos x=\frac{1} {2}(e^{jx}+e^{-jx})\)↩︎