一种基于纯C语言的函数绘图解决方案

本文尝试实现一种利用C语言绘制函数图像的方法。最终输出为PPM格式图片。

一、PPM图片格式

我们首先来看一下我们的问题：怎么用纯C语言写一个plot()函数。那么我们迎面而来遇到的第一个问题就是：我们平常使用的C语言，往往是在一个黑框框里面输入一堆数字，然后输出一堆数字，而现在却要展示一张图片，这怎么做呢？但是我们静下心来想一想，就会发现所谓的图片实际上也是文件，而文件就是可以用C语言的freopen读写的。但是我们平时读写的都是纯文本文件，现在却要写入一张图片文件。怎么做到呢？这时就需要一种非常简单的图片编码：PPM格式。

PPM格式是 Netpbm [1]的一部分。这个项目使用和定义了几种图形格式。便携式像素映射格式（PPM）、便携式灰图格式（PGM） 和便携式位图格式（PBM） ，旨在便于在平台之间交换。

一个PPM文件由两部分组成，即文件头和数据流。文件头的第一部分是一个Magic Number，格式为P%d，表示了文件的类型，具体如下表所示：

类型 ASCII （普通） 二进制（原始）
便携式位图（PBM） P1 P4
便携式灰度图（PGM） P2 P5
便携式像素映像（PPM） P3 P6

文件头的第二部分是两个数字，表示了图像的宽度和高度。

而PGM和PPM文件的文件头有第三部分，是一个数字，表示颜色（分量）的最大值。

数据流部分是以矩阵形式显示的像素点。接下来我们看几个例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
P1
# This is an example bitmap of the letter "J"
6 10
0 0 0 0 1 0
0 0 0 0 1 0
0 0 0 0 1 0
0 0 0 0 1 0
0 0 0 0 1 0
0 0 0 0 1 0
1 0 0 0 1 0
0 1 1 1 0 0
0 0 0 0 0 0
0 0 0 0 0 0
123

这是一个PBM（位图）格式的文件，其中0表示白色，1表示黑色。显示成图片的话是这个样子（放大了20倍）

1
2
3
4
5
6
7
8
9
10
11
P2
# Shows the word "FEEP" (example from Netpbm man page on PGM)
24 7
15
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
0  3  3  3  3  0  0  7  7  7  7  0  0 11 11 11 11  0  0 15 15 15 15  0
0  3  0  0  0  0  0  7  0  0  0  0  0 11  0  0  0  0  0 15  0  0 15  0
0  3  3  3  0  0  0  7  7  7  0  0  0 11 11 11  0  0  0 15 15 15 15  0
0  3  0  0  0  0  0  7  0  0  0  0  0 11  0  0  0  0  0 15  0  0  0  0
0  3  0  0  0  0  0  7  7  7  7  0  0 11 11 11 11  0  0 15  0  0  0  0
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0

这个一个PGM（灰度图）的例子，我们可以看到第四行，这就是所谓“颜色（分量）的最大值”。它对应的图片是这个样子（当然也经过了放大）：

1
2
3
4
5
6
7
8
9
10
11
P3           # "P3" means this is a RGB color image in ASCII
3 2          # "3 2" is the width and height of the image in pixels
255          # "255" is the maximum value for each color
# The part above is the header
# The part below is the image data: RGB triplets
255   0   0  # red
  0 255   0  # green
  0   0 255  # blue
255 255   0  # yellow
255 255 255  # white
  0   0   0  # black

这是一个PPM图片的例子，我们可以看到每个像素点使用了三个数字来指定颜色，也就是我们所说的RGB。

到这里，你应该已经掌握了PPM格式图片怎么写了吧！

二、定义函数表

为了方便绘图，首先我们定义PPM数据类型，由RGB三个颜色分量组成。

1
2
3
typedef struct {
    int r, g, b;
} PPMdata;

这个结构体的构造函数为：

1
PPMdata makePPMdata(int r, int g, int b);

主要执行绘图功能的函数为：

1
2
3
4
5
6
7
8
9
10
11
12
13
int arrayToPPM(char *name,
               PPMdata **matrix,
               const double *x,
               double *y,
               int width,
               int height,
               int arrayLen,
               double centerX,
               double centerY,
               double rangeX,
               double rangeY,
               double gridX,
               double gridY);

其中各参数的意义如下：

项目 意义
char *name 输出文件的文件名
PPMdata **matrix PPM文件流矩阵，大小至少为height*width
const double *x 采样点x坐标
double *y 采样点y坐标
int width 整个图像的宽度 单位：像素
int height 整个图像的高度 单位：像素
int arrayLen 采样点的数目
double centerX 图片中心点对应的直角坐标X
double centerY 图片中心点对应的直角坐标Y
double rangeX X直角坐标范围
double rangeY Y直角坐标范围
double gridX X网格宽度（单位：直角坐标）
double gridY Y网格宽度（单位：直角坐标）

将直角坐标量转化为像素量（矩阵下标量）的函数为：

1
int numToMatPos(double num, double center, double range, double picLen);

其中各参数的意义为：

项目 意义
double num 待转换的直角坐标量x
double center 图片该方向中心点对应的直角坐标c
double range 该方向直角坐标范围r
int picLen 图片该方向的像素大小p

转换公式为： \[ p\left(\frac 12+\frac{x-c}{r}\right) \] 在图像上绘制坐标点的函数为：

1
void drawPoint(PPMdata **matrix, int width, int height, int x, int y, PPMdata color, int size)

各新参数的意义如下：

项目 意义
int x 要绘制的点的像素X坐标
int y 要绘制的点的像素Y坐标
PPMdata color 颜色
int size 点的大小，最后绘制出来是一个\(2size+1\)边长的正方形

将PPMdata数据矩阵转换为.ppm图像文件的函数如下：

1
void matToPPM(char *fileName,PPMdata **matrix, int width, int height);

没有新的参数。

由于绘图时采用分段线性拟合算法，定义线性函数：

1
#define linerFunc(x1,y1,x2,y2,x) ((x-x1)*(y2-y1)/(x2-x1)+y1)

这个定义的意思是：\(y=\text{linerFunc}(x_1,y_1,x_2,y_2,x)\)表示一条经过\((x_1,y_2)\)和\((x_2,y_2)\)，以\(x\)为自变量的直线。直线方程为： \[ y=(x-x_1)\frac{y_2-y_1}{x_2-x_1}+y_1 \]

三、实现函数

这部分以arrayToPPM()函数的实现为主线，完整介绍各个函数的实现方法。

第一步，检测数据的合法性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
if (height % 2) ++height;
if (width % 2) ++width;
for (int i = 0; i < arrayLen; ++i) {
    if (x[i] < x[i - 1] && i >= 1) {
        fprintf(stderr, "ERROR: X is not increasing.\n");
        return -1;
    }
    if (!(x[i] > centerX - (rangeX / 2.0) && x[i] < centerX + (rangeX / 2.0))) {
        fprintf(stderr, "ERROR: X out of range.\n");
        return -1;
    }
    if (!(y[i] > centerY - (rangeY / 2.0) && y[i] < centerY + (rangeY / 2.0))) {
        if (y[i] > centerY + (rangeY / 2.0)) y[i] = centerY + (rangeY / 2.0);
        if (y[i] < centerY - (rangeY / 2.0)) y[i] = centerY - (rangeY / 2.0);
    }
}

首先，为了方便，我们强制把像素大小设置为偶数。然后主要检查三个事：

  1. \(x\)坐标是否严格单调递增。若不是，返回错误并退出。
  2. \(x\)坐标是否在范围内。若不是，返回错误并退出。
  3. \(y\)坐标是否在范围内。若不是，强制将其设置在范围内。

第二步，定义PPMdata颜色。

1
2
3
4
5
PPMdata background, axis, grid, line;
background = makePPMdata(255, 255, 251);
axis = makePPMdata(28, 28, 28);
grid = makePPMdata(189, 192, 186);
line = makePPMdata(0, 92, 175);

各变量的意义如下：

项目 意义
background 背景颜色
axis 主坐标轴颜色
grid 网格颜色
line 要画的函数的颜色

这里就用配色软件找一个好看的颜色就行。

第三步，绘制背景板

  1. 画背景

    1
    2
    3
    4
    5
    for (int i = 0; i < height; ++i) {
        for (int j = 0; j < width; ++j) {
            matrix[i][j] = background;
        }
    }

  2. 画网格

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    for (int i = 0; centerX + i * gridX <= centerX + rangeX / 2; ++i) {
        for (int j = 0; j < height; ++j) {
            drawPoint(matrix, width, height, numToMatPos(centerX + i * gridX, centerX, rangeX, width), j, grid, 0);
            drawPoint(matrix, width, height, numToMatPos(centerX - i * gridX, centerX, rangeX, width), j, grid, 0);
        }
    }//纵向网格
    for (int i = 0; centerY + i * gridY <= centerY + rangeY / 2; ++i) {
        for (int j = 0; j < width; ++j) {
            drawPoint(matrix, width, height, j, numToMatPos(centerY + i * gridY, centerY, rangeY, height), grid, 0);
            drawPoint(matrix, width, height, j, numToMatPos(centerY - i * gridY, centerY, rangeY, height), grid, 0);
        }
    }//横向网格

  3. 画主坐标轴

    1
    2
    3
    4
    5
    6
    7
    for (int i = 0; i < width; ++i) {
        drawPoint(matrix, width, height, i, height / 2, axis, 1);
    }

    for (int i = 0; i < height; ++i) {
        drawPoint(matrix, width, height, width / 2, i, axis, 1);
    }

    这里的“主坐标轴”，恒定位于图像的正中心。

这里涉及到了drawPoint()函数。它的实现如下：

1
2
3
4
5
6
7
8
9
void drawPoint(PPMdata **matrix, int width, int height, int x, int y, PPMdata color, int size) {
    for (int i = -1 * size; i <= size; ++i) {
        for (int j = -1 * size; j <= size; ++j) {
            int u = x + i, v = y + j;
            if (u >= width || u < 0 || v >= height || v < 0) return;
            else matrix[v][u] = color;
        }
    }
}

主要还是要检测是不是越界了，不然容易RE.还有一个需要注意的地方就是第6行，这里的x和y互换了。为什么要互换呢？我们想一想矩阵下标的顺序和坐标的顺序有什么区别就好了。

第四步，画函数

我们经过了这么长的准备，终于要开始画函数了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
double stepX = rangeX / width;
for (double X = centerX - rangeX / 2; X < centerX + rangeX / 2; X += stepX) {
    int linerIndex = -1;
    for (int i = 0; i < arrayLen; ++i) {
        if (X < x[i]) {
            linerIndex = i - 1;
            break;
        }
    }
    if (linerIndex == -1) {
        continue;
    } else {
        double u, v, Y;
        u = numToMatPos(X, centerX, rangeX, width);
        Y = linerFunc(x[linerIndex], y[linerIndex], x[linerIndex + 1], y[linerIndex + 1], X);
        v = numToMatPos(Y, centerY, rangeY, height);
        drawPoint(matrix, width, height, u, v, line, 1);
    }
}

既然我们用的是分段线性拟合法，那么就要确认当前在哪个段里，也就是代码中的linerIndex变量。

X就是枚举变量。如果当前比x[]数列中的最小值还小，那么不应该有图像，否则找到当前所在的段，然后画一条线段。

第五步，写文件

1
matToPPM(name, matrix, width, height);

这里matToPPM函数的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void matToPPM(char *fileName, PPMdata **matrix, int width, int height) {
    freopen(fileName, "w", stdout);
    printf("P3\n");
    printf("%d %d\n", width, height);
    printf("255\n");
    for (int i = 0; i < height; ++i) {
        for (int j = 0; j < width; ++j) {
            printf("%d %d %d", matrix[i][j].r, matrix[i][j].g, matrix[i][j].b);
            printf(" ");
        }
        printf("\n");
    }
    fclose(stdout);
    freopen("CON", "w", stdout);
    return;
}

就是重定向，输出，再重定向回来，没什么特别值得说明的。

四、试用一下

我们把上面那一堆函数和实现打包到一个.h文件里。然后我们写个代码调用一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include "arrayToPPM.h"

int main() {
    double x[1001], y[1001];
    int cnt = 0;
    for (double i = -10.0; i <= 10.0; i += 0.1) {
        x[cnt] = i;
        y[cnt] = sin(i*2.0)/(i*2.0);
        ++cnt;
    }
    //创建matrix 矩阵
    PPMdata **matrix = (PPMdata **) malloc(sizeof(PPMdata *) * 1080);
    for (int i = 0; i < 1080; i++) 
        matrix[i] = (PPMdata *) calloc(1920, sizeof(PPMdata));
    char c[]="out.ppm";
    arrayToPPM(c, matrix, x, y, 1920, 1080, cnt, 0, 0, 21, 4, 3.14159/4.0, 0.5);
    printf("complete.\n");
    return 0;
}

这个代码的功能是绘制 \[ y=\frac{\sin 2x}{2x} \] 的图像。

编译运行，在目录下输出了一个out.ppm文件，打开：

大功告成咯！

五、更多讨论

这个代码存在以下问题：

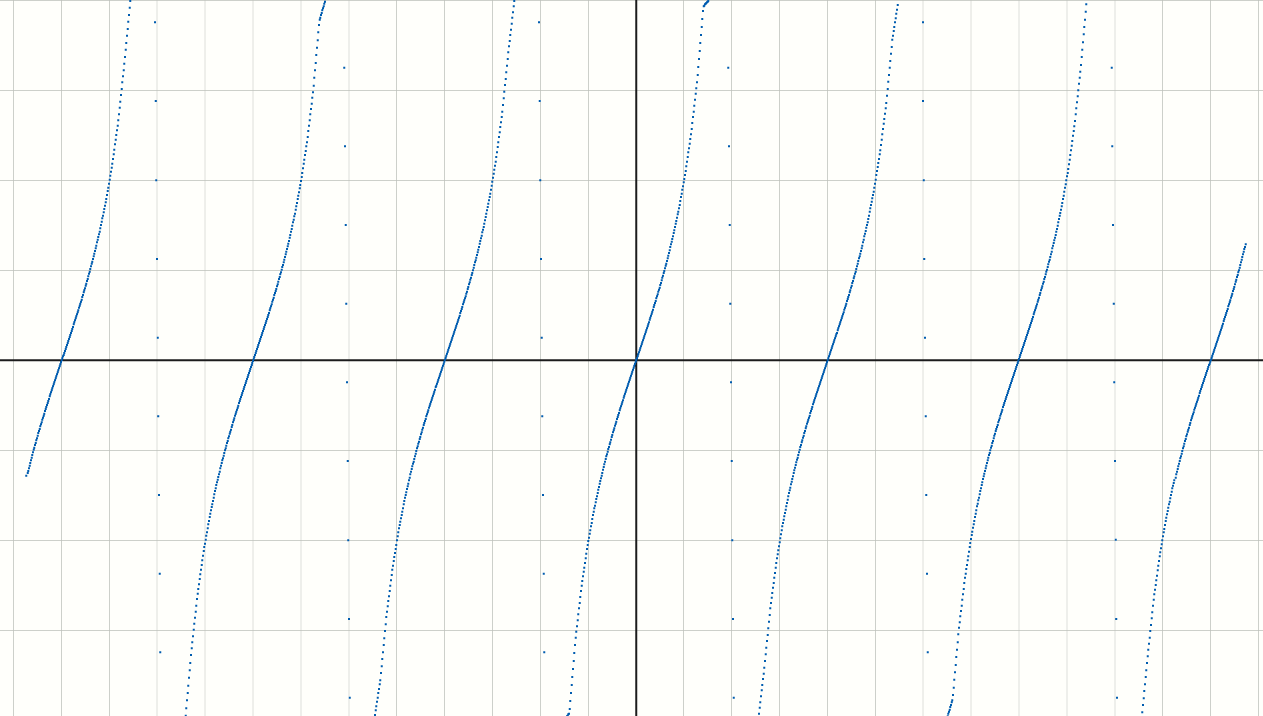
  1. 面对函数变化率特别高的情况下表现不理想，会有间断的情况，如下图所示：

\[ y=\tan x \]

  1. 需要人工指定的变量太多，日后我会开发一版能自动适应采样点，选择合适的坐标、范围的绘图函数。

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

image-20250112002710775
  1. https://en.wikipedia.org/wiki/Netpbm#File_formats ↩︎
技术
#C #信号与系统
一种基于纯C语言的函数绘图解决方案
https://suzumiyaakizuki.github.io/2022/05/16/一种基于纯C语言的函数绘图解决方案/
作者
SuzumiyaAkizuki
发布于
2022年5月16日
许可协议