信号与系统实验1：连续时间系统卷积的数值计算

这是信号与系统的实验报告。我信号与系统总共就扣了几分，也不知道是期末扣的，还是实验扣的。即使全是实验扣的，这实验也算做的挺好的。于是把报告发出来给大家参考。 这是第一个实验，连续时间系统卷积的数值计算

一、实验原理

卷积积分不仅可以通过直接积分或查表的方法来求解，还可以用积分的数值计算方法来求解。在线性系统的分析过程中，有时会遇到复杂的激励信号，或者有时只是一组测试数据或曲线，冲激响应也可能出现同样的情况。显然，此时直接计算积分或查表都有困难，而采用近似的数值计算方法可以解决这个问题，求得卷积积分。

两个信号\(f_1(t)\)和\(f_2(t)\)的卷积\(f_1(t)*f_2(t)\)定义为： \[ f_1(t)*f_2(t)=\int_{-\infty}^{\infty}f_1(t-\tau)f_2(\tau){\bf d}\tau \] 在计算卷积积分时，我们通常采取“翻转→平移→相乘→叠加”的方法。

1. 将信号取值离散化，即以 Ts 为周期，对信号取值，得到一系列宽度间隔为 Ts 的矩形脉冲原信号的离散取值点，用所得离散取值点矩形脉冲来表示原来的连续时间信号；

2. 将进行卷积的两个信号序列之一反转，与另一信号相乘，并求积分，所得为 t=0 时的卷积积分的值。以 Ts 为单位左右移动反转的信号，与另一信号相乘求积分，求的 t<0 和 t>0 时卷积积分的值；

3. 将所得卷积积分值与对应的 t 标在图上，连成一条光滑的曲线，即为所求卷积积分的曲线。

上述过程，在形式上，就是用 \[ \sum_{\tau=\tau_0}^{\tau_1}f_1(t-\tau)f_2(\tau)\Delta\tau \] 来逼近\(f_1(t)*f_2(t)\)。其中\(\tau_0\)是一个很小的值，\(\tau_1\)是一个很大的值，\(\Delta \tau\)是每次\(\tau\)增加的值。

二、实验内容

\[ f_1(t)=u(t+2)-u(t-2)\\ f_2(t)=t[u(t)-u(t-2)]+(4-t)[u(t-2)-u(t-4)] \]

用数值方法计算\(f_1*f_2\)，将结果用表格列出，并画出图像。

三、实验过程

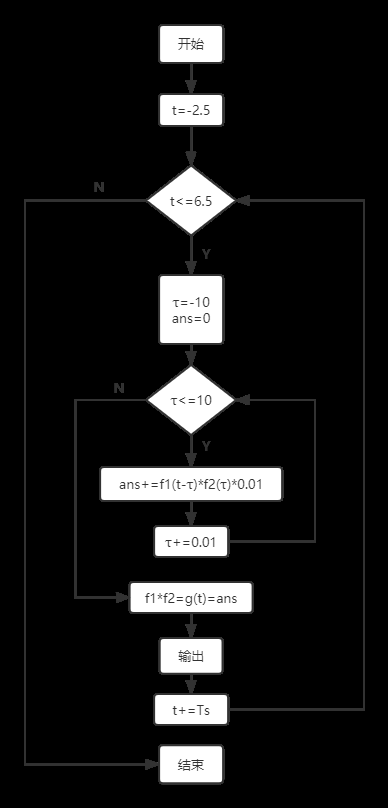
1. 程序框图

image-20220709162415460

2. 程序代码

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <ctype.h>
#include <stdlib.h>
const double eps = 1e-11;
const double dt = 0.1;

inline double u(double t) {
	return (t > 0.0) ? 1.0 : 0.0;
}

inline double f1(double t) {
	return u(t + 2) - u(t - 2);
}

inline double f2(double t) {
	return t * 1.0 * (u(t) - u(t - 2)) + (4 - t) * 1.0 * (u(t - 2) - u(t - 4));
}

int main() {
	freopen("ans.xls","w+",stdout);
	for (double t = -2.5; t <= 6.5; t += dt) {
		double ans = 0.0;
		for (double i = -10.0; i <= 10.0; i += 0.01) {
			ans += f1(t - i) * f2(i) * 0.01;
		}
		printf("%.3f\t%.3f\n", t, ans);
	}
	return 0;
}

3. 运行结果

部分表格：

其中\(g(t)=f_1(t)*f_2(t)\)

\(t\)	\(g(t)\)	\(t\)	\(g(t)\)
-2	0	2.1	3.995
-1.9	0.005	2.2	3.981
-1.8	0.019	2.3	3.957
-1.7	0.044	2.4	3.922
-1.6	0.078	2.5	3.877
-1.5	0.123	2.6	3.823
-1.4	0.177	2.7	3.758
-1.3	0.242	2.8	3.684
-1.2	0.316	2.9	3.599
\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)

完整表格下载地址：

实验结果

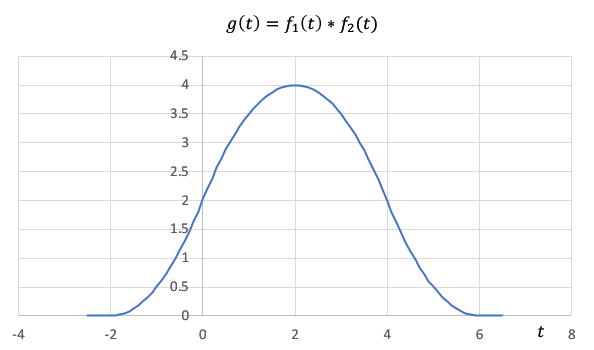
绘制图像：

image-20220405220304046

使用Excel 365软件绘制图像。

四、解析求解和误差分析

使用符号计算语言Mathematica运行下列代码：

f1 = UnitStep[t + 2] - UnitStep[t - 2];
f2 = t*(UnitStep[t] - UnitStep[t - 2]) + (4 - t)*(UnitStep[t - 2] - 
      UnitStep[t - 4]);
g = Convolve[f1, f2, t, \[Tau]];
Plot[g, {\[Tau], -4, 8}]
PiecewiseExpand[g]

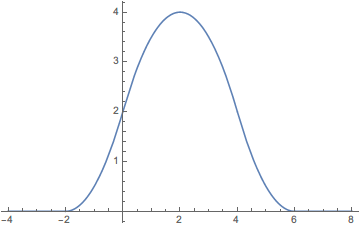
可以得到卷积结果的解析式为： \[ g(\tau)=\begin{cases} \frac{1}{2} (\tau +2)^2 & -2\leq \tau <0 \\[1.5ex] \frac{1}{2} \left(-\tau ^2+4 \tau +4\right) & 0\leq \tau <4 \\[1.5ex] \frac{1}{2} \left(\tau ^2-12 \tau +36\right) & 4\leq \tau <6 \\[1.5ex] 0 & \text{others} \end{cases} \] 画出的图像为：

image-20220709163735914

将其代入程序，可计算得数值算法的均方误差 \[ \begin{aligned} \text{MSE}&=\sum_{i=1}^n[ans_i-g(t_i)]^2\\ &=0.000029 \end{aligned} \] 计算代码如下：

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <ctype.h>
#include <stdlib.h>
const double eps = 1e-11;
const double dt = 0.1;

inline double u(double t) {
	return (t > 0.0) ? 1.0 : 0.0;
}

inline double f1(double t) {
	return u(t + 2) - u(t - 2);
}

inline double f2(double t) {
	return t * 1.0 * (u(t) - u(t - 2)) + (4 - t) * 1.0 * (u(t - 2) - u(t - 4));
}

inline double g(double t){
	if(t>=-2 && t<=0) return (t+2.0)*(t+2.0)*0.5;
	else if(0<t && t<=4) return (-t*t+4.0*t+4.0)*0.5;
	else if(4<t && t<=6) return (t*t-12.0*t+36.0)*0.5;
	else return 0;
}

int main() {
	freopen("ans.xls","w+",stdout);
	double e=0.0;
	int cnt=0;
	for (double t = -2.5; t <= 6.5; t += dt) {
		double ans = 0.0;
		for (double i = -10.0; i <= 10.0; i += 0.01) {
			ans += f1(t - i) * f2(i) * 0.01;
		}
		printf("%.3f\t%.3f\n", t, ans);
		e+=(ans-g(t))*(ans-g(t));
		++cnt;
	}
	fclose(stdout);
	freopen("CON","w",stdout);
	printf("MSE = %f",e/(cnt*1.0));
	return 0;
}